วิธีการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์บนเครื่องคิดเลข ti-84
ค่าสัมประสิทธิ์สหสัมพันธ์ คือการวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว สามารถรับค่าระหว่าง -1 ถึง 1 โดยที่:
- -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
- 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
- 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
คุณสามารถใช้ขั้นตอนต่อไปนี้เพื่อคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรสองตัวบนเครื่องคิดเลข TI-84:
ขั้นตอนที่ 1: เปิดใช้งานการวินิจฉัย
ขั้นแรกเราต้องเปิดใช้งานการวินิจฉัย โดยกด 2 แล้วกดเลข 0 ซึ่งจะพาเราไปที่หน้าจอ CATALOG

เลื่อนไปที่ DiagnosticOn แล้วกด ENTER
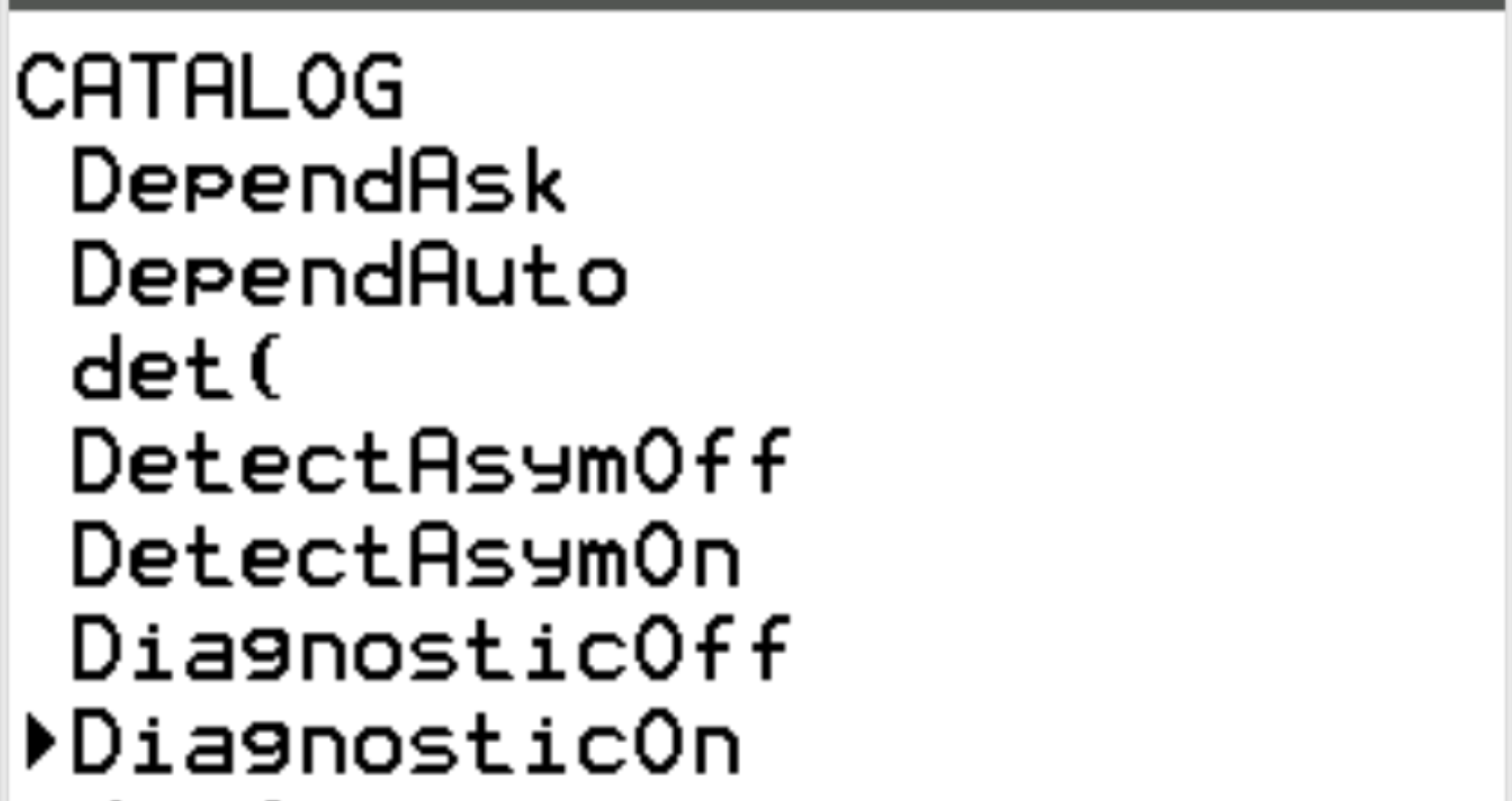
จากนั้น กด ENTER อีกครั้ง
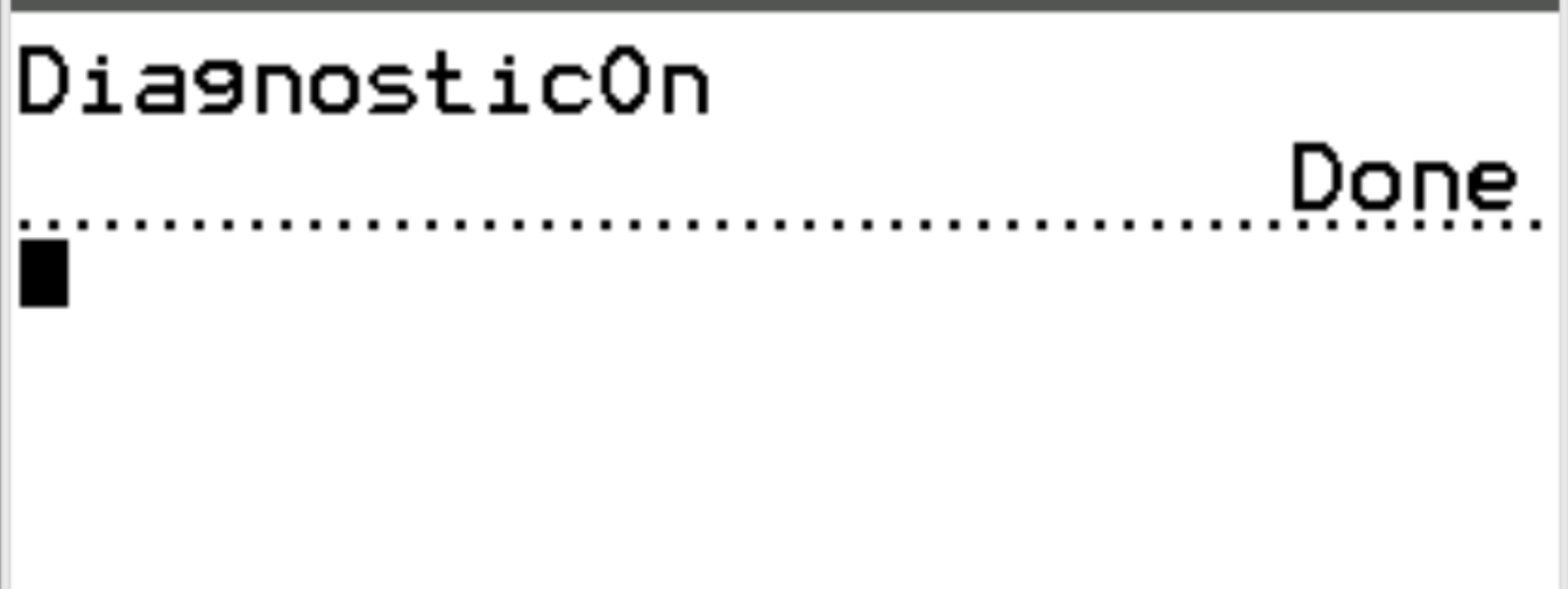
ขณะนี้การวินิจฉัยเปิดใช้งานแล้ว เพื่อให้เราสามารถคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรสองตัวได้
ขั้นตอนที่ 2: ป้อนข้อมูล
ต่อไปเราต้องใส่ค่าข้อมูลสำหรับตัวแปรทั้งสองของเรา กด Stat จากนั้นกด EDIT ป้อนค่าของตัวแปรแรกในคอลัมน์ L1 และค่าของตัวแปรที่สองในคอลัมน์ L2:
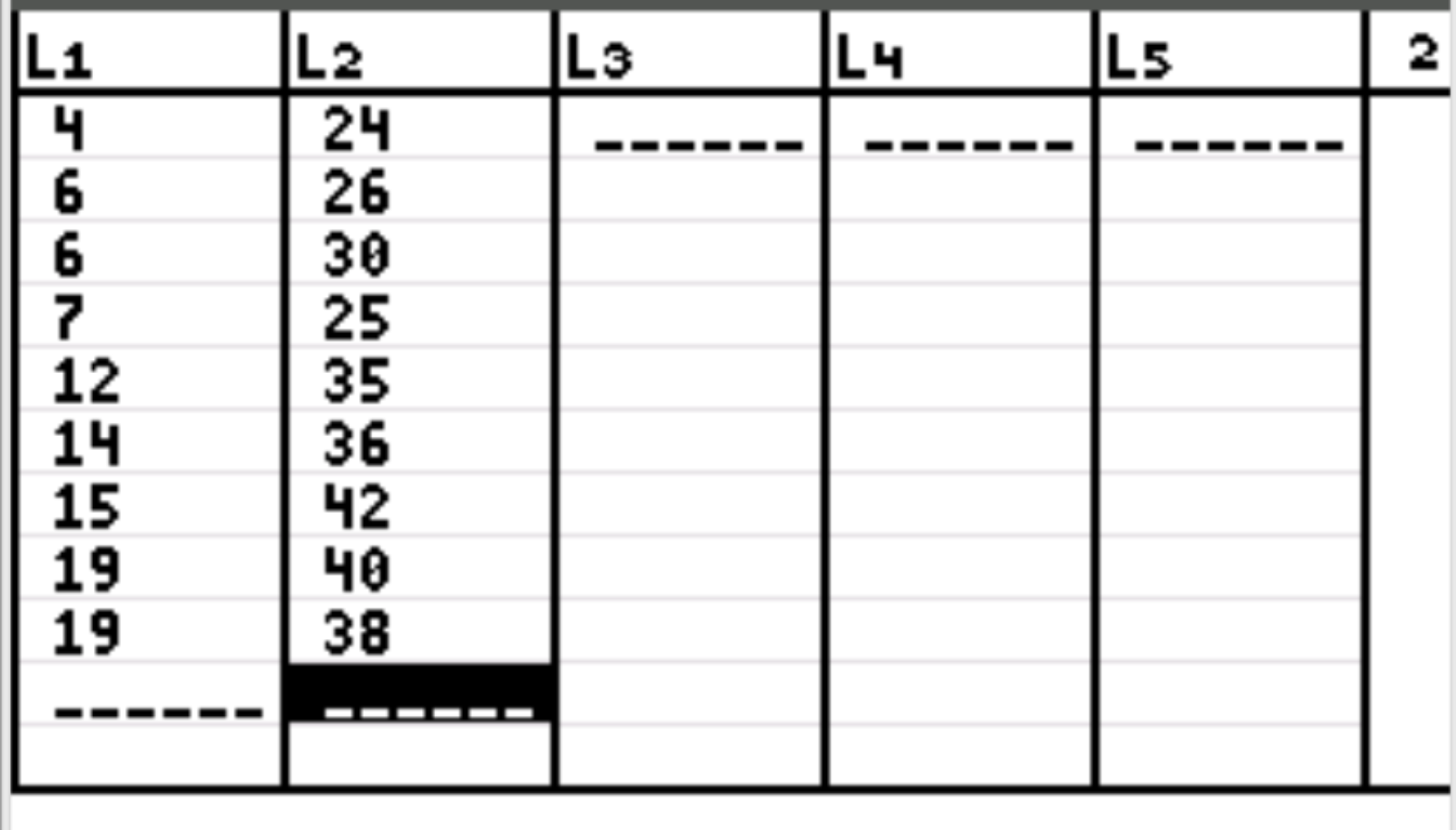
ขั้นตอนที่ 3: ค้นหาค่าสัมประสิทธิ์สหสัมพันธ์
ต่อไป เราจะคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรทั้งสอง กด Stat จากนั้นเลื่อนไปที่ CALC จากนั้นเลื่อนไปที่ 8: Linreg(a+bx) แล้วกด Enter
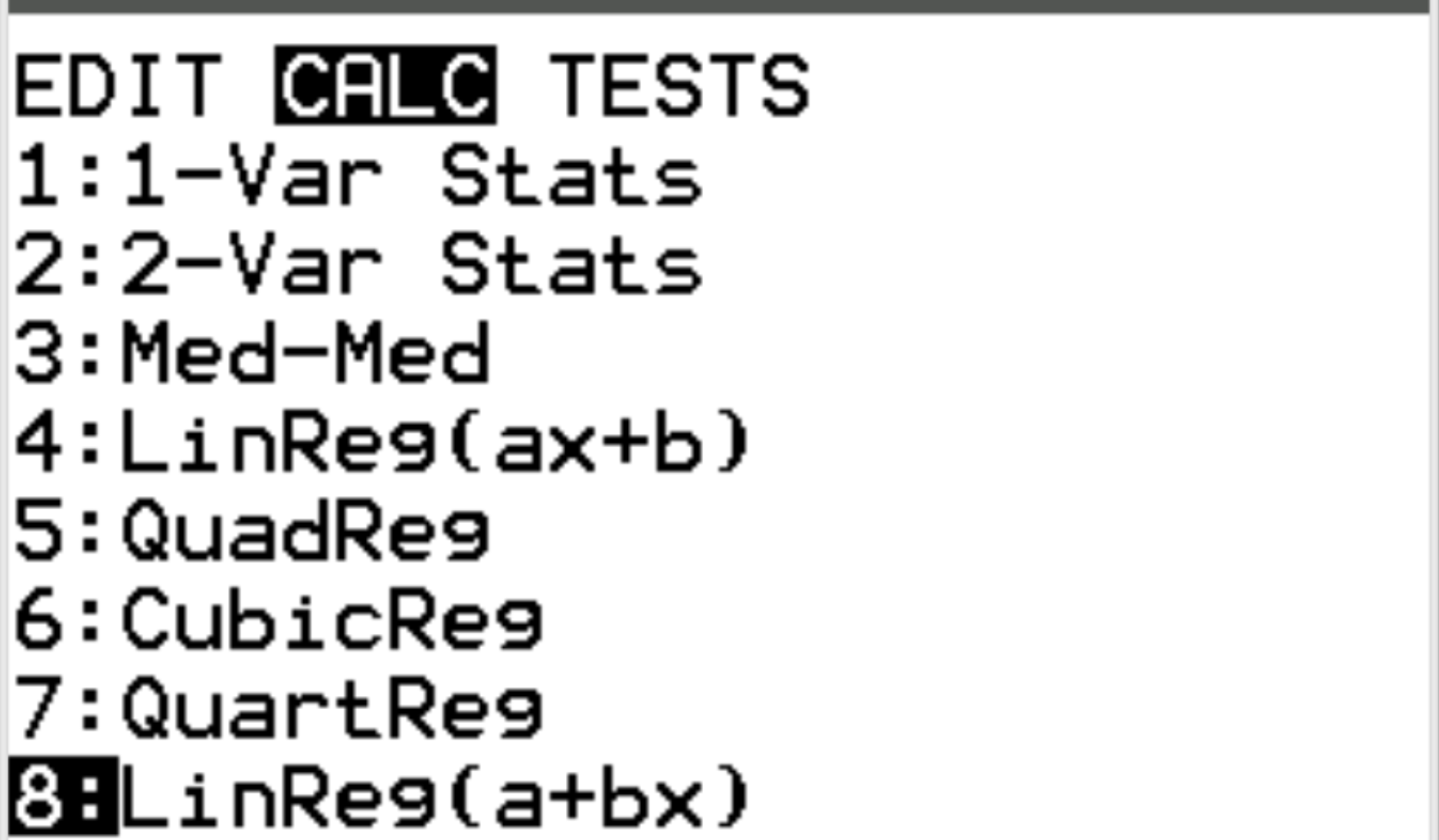
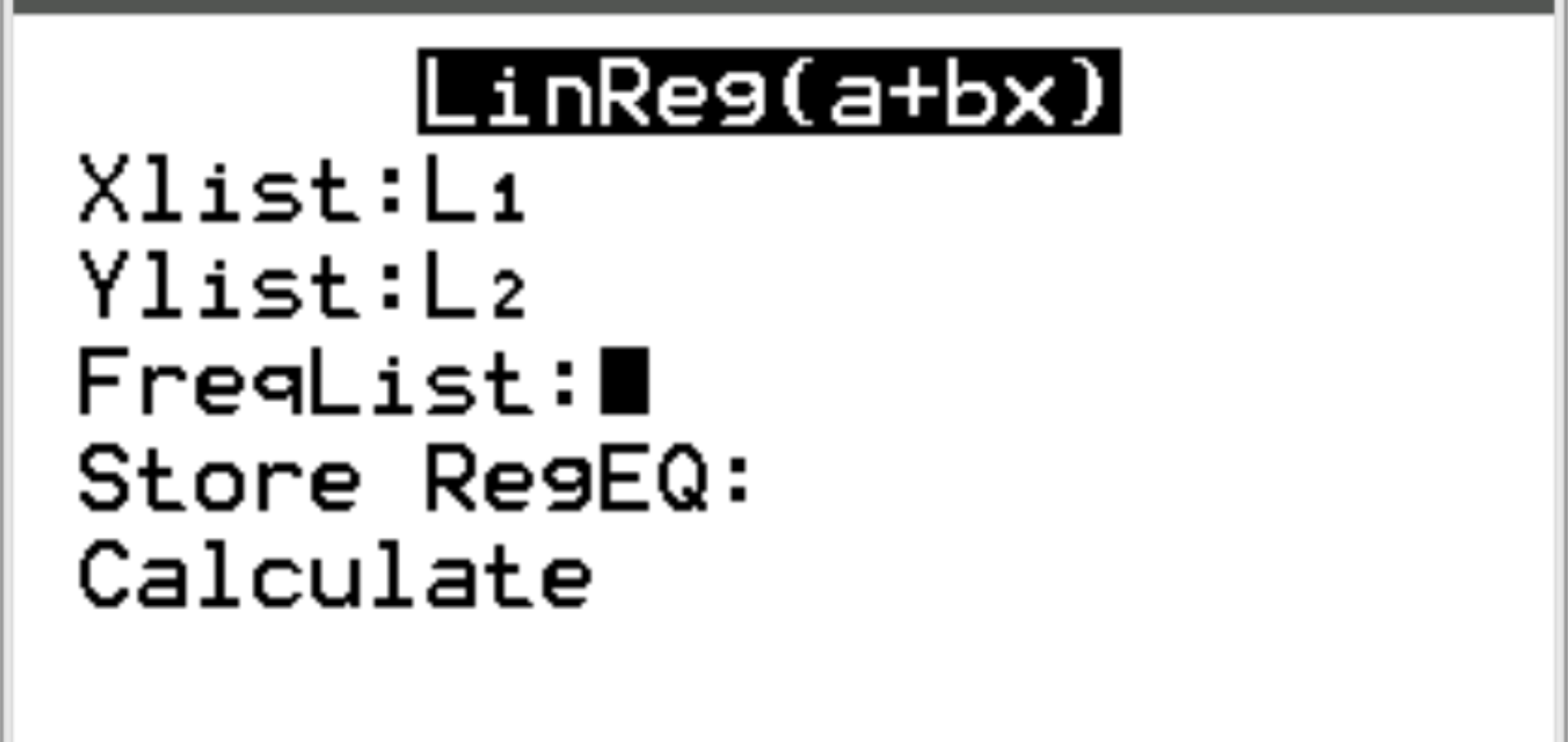
สำหรับ Xlist และ Ylist ตรวจสอบให้แน่ใจว่าได้เลือก L1 และ L2 เนื่องจากเป็นคอลัมน์ที่เราใช้ในการป้อนข้อมูลของเรา ปล่อย FreqList ว่างไว้ เลื่อนลงไปที่ คำนวณ แล้วกด Enter
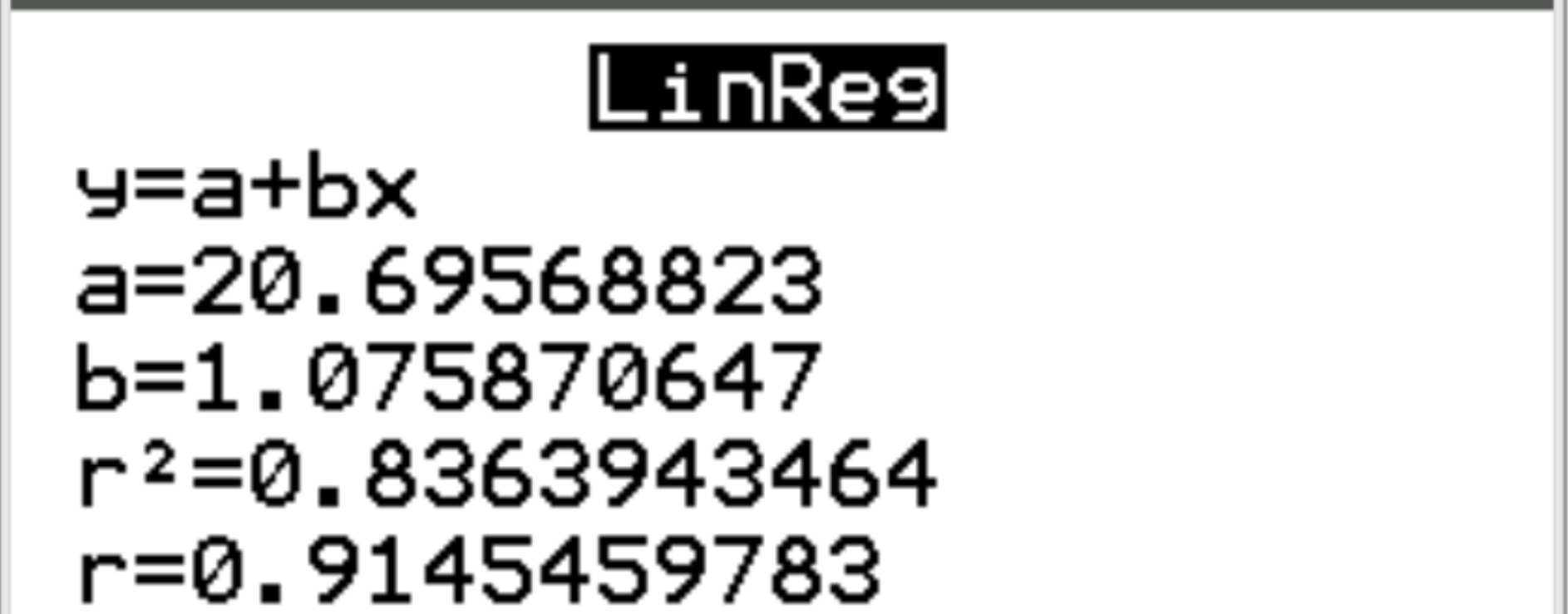
บนหน้าจอใหม่ เราจะเห็นว่าค่าสัมประสิทธิ์สหสัมพันธ์ (r) ระหว่างตัวแปรทั้งสองคือ 0.9145
วิธีการตีความค่าสัมประสิทธิ์สหสัมพันธ์
ตารางต่อไปนี้แสดงกฎทั่วไปสำหรับการตีความจุดแข็งของความสัมพันธ์ระหว่างตัวแปรสองตัวตามค่าของ r :
| ค่าสัมบูรณ์ของ r | ความแข็งแกร่งของความสัมพันธ์ |
|---|---|
| อาร์ < 0.25 | ไม่มีความสัมพันธ์ |
| 0.25 < ร < 0.5 | ความสัมพันธ์ที่อ่อนแอ |
| 0.5 < ร < 0.75 | ความสัมพันธ์ระดับปานกลาง |
| ร > 0.75 | ความสัมพันธ์ที่แข็งแกร่ง |
ในตัวอย่างของเรา ค่าสัมประสิทธิ์สหสัมพันธ์ 0.9145 บ่งชี้ถึงความสัมพันธ์เชิงบวกที่แข็งแกร่งระหว่างตัวแปรทั้งสอง