วิธีการคำนวณความน่าจะเป็นแบบทวินามบนเครื่องคิดเลข ti-84
การแจกแจงแบบทวินาม เป็นหนึ่งในการแจกแจงที่ใช้บ่อยที่สุดในสถิติทั้งหมด บทช่วยสอนนี้จะอธิบายวิธีใช้ฟังก์ชันต่อไปนี้ในเครื่องคิดเลข TI-84 เพื่อค้นหาความน่าจะเป็นแบบทวินาม:
binompdf(n, p, x) ส่งคืนความน่าจะเป็นที่เกี่ยวข้องกับไฟล์ pdf ทวินาม
binomcdf(n, p, x) ส่งกลับค่าความน่าจะเป็นสะสมที่เกี่ยวข้องกับ cdf ทวินาม
ทอง:
- n = จำนวนการทดลอง
- p = ความน่าจะเป็นที่จะประสบความสำเร็จในการทดลองที่กำหนด
- x = จำนวนความสำเร็จทั้งหมด
ฟังก์ชันทั้งสองนี้สามารถเข้าถึงได้บนเครื่องคิดเลข TI-84 โดยกด 2 แล้วกด vars สิ่งนี้จะนำคุณไปยังหน้าจอ DISTR ซึ่งคุณสามารถใช้ binompdf() และ binomcdf() :
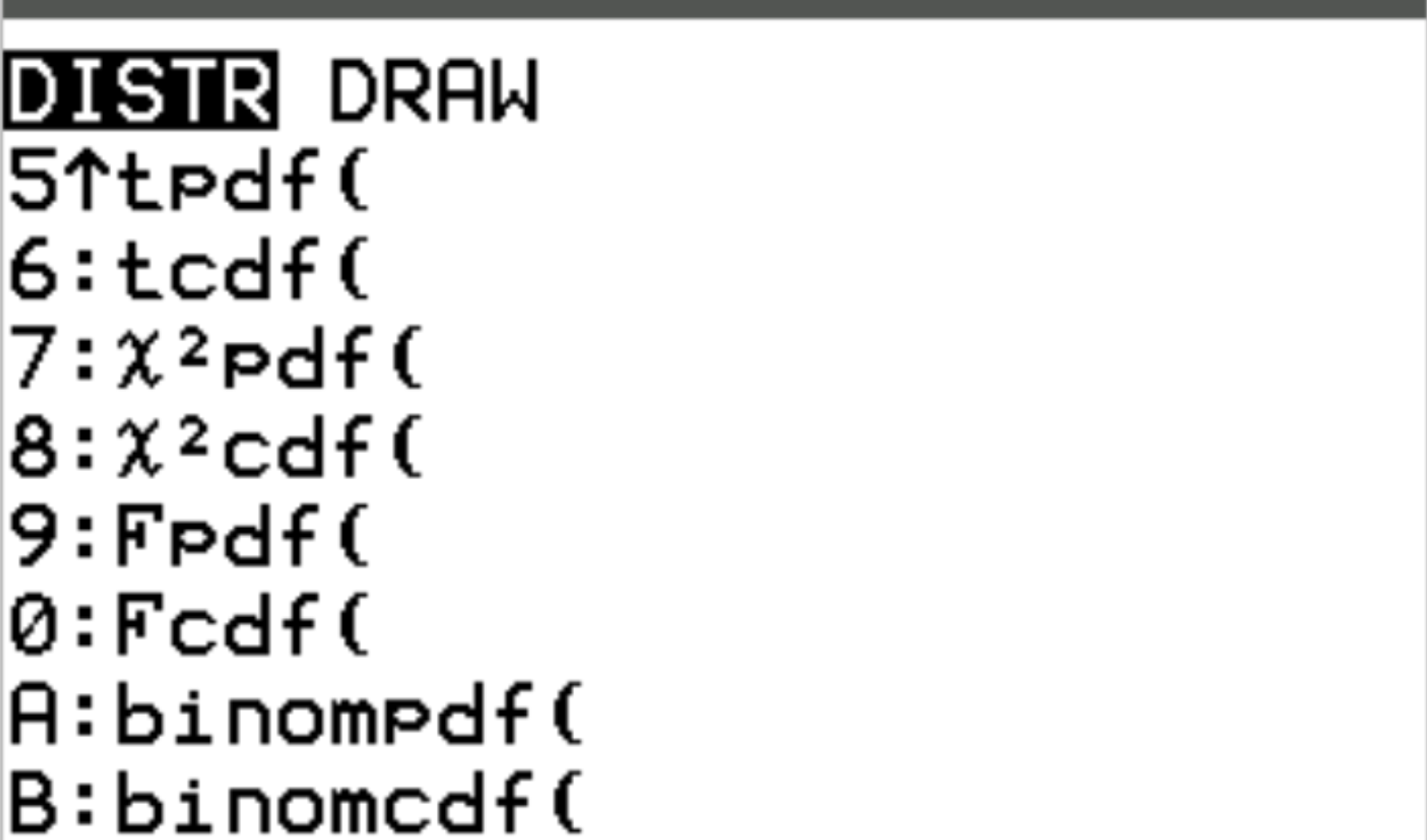
ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันเหล่านี้เพื่อตอบคำถามต่างๆ
ตัวอย่างที่ 1: ความน่าจะเป็นทวินามของความสำเร็จ x พอดี
คำถาม: นาธานพยายามโยนโทษ 60% ถ้าเขาโยนโทษ 12 ครั้ง ความน่าจะเป็นที่เขาโยนโทษได้ 10 ครั้งพอดีเป็นเท่าใด?
คำตอบ: ใช้ฟังก์ชันทวินามpdf(n, p, x):
ทวินามpdf(12, .60, 10) = 0.0639
ตัวอย่างที่ 2: ความน่าจะเป็นแบบทวินามที่น้อยกว่า x สำเร็จ
คำถาม: นาธานพยายามโยนโทษ 60% ถ้าเขาโยนโทษ 12 ครั้ง ความน่าจะเป็นที่เขาทำได้น้อยกว่า 10 ครั้งเป็นเท่าใด
คำตอบ: ใช้ฟังก์ชัน ทวินามcdf(n, p, x-1) :
ทวินามcdf(12, .60, 9) = 0.9166
ตัวอย่างที่ 3: ความน่าจะเป็นทวินามที่จะสำเร็จสูงสุด x
คำถาม: นาธานพยายามโยนโทษ 60% ถ้าเขาโยนโทษ 12 ครั้ง ความน่าจะเป็นที่เขาทำได้มากที่สุด 10 ครั้งจะเป็นเท่าใด
คำตอบ: ใช้ฟังก์ชัน ทวินามcdf(n, p, x) :
ทวินามcdf(12, .60, 10) = 0.9804
ตัวอย่างที่ 4: ความน่าจะเป็นแบบทวินามที่ประสบความสำเร็จมากกว่า x
คำถาม: นาธานพยายามโยนโทษ 60% ถ้าเขาโยนโทษ 12 ครั้ง ความน่าจะเป็นที่เขาทำได้มากกว่า 10 ครั้งเป็นเท่าใด
คำตอบ: ใช้ฟังก์ชัน 1 – binomialcdf(n, p, x) :
1 – ทวินามซีดีเอฟ(12, .60, 10) = 0.0196
ตัวอย่างที่ 5: ความน่าจะเป็นแบบทวินามที่ประสบความสำเร็จอย่างน้อย x
คำถาม: นาธานพยายามโยนโทษ 60% ถ้าเขาโยนโทษ 12 ครั้ง ความน่าจะเป็นที่เขาทำได้มากกว่า 10 ครั้งเป็นเท่าใด
คำตอบ: ใช้ฟังก์ชัน 1 – binomialcdf(n, p, x-1) :
1 – ทวินามซีดีเอฟ(12, .60, 9) = 0.0834