ส่วนเบี่ยงเบนมาตรฐานสัมพัทธ์
บทความนี้จะอธิบายวิธีคำนวณค่าเบี่ยงเบนมาตรฐานสัมพัทธ์ คุณจะพบว่าค่าเบี่ยงเบนมาตรฐานสัมพัทธ์คืออะไร สูตรของมันคืออะไร ตลอดจนแบบฝึกหัดที่แก้ไขทีละขั้นตอน
ค่าเบี่ยงเบนมาตรฐานสัมพัทธ์คืออะไร?
ค่าเบี่ยงเบนมาตรฐานสัมพัทธ์ คือการวัดทางสถิติที่ระบุการกระจายตัวของชุดข้อมูลที่สัมพันธ์กับค่าเฉลี่ย ค่าเบี่ยงเบนมาตรฐานสัมพัทธ์คำนวณโดยการหารค่าเบี่ยงเบนมาตรฐานของข้อมูลด้วยค่าเฉลี่ย
ค่าเบี่ยงเบนมาตรฐานสัมพัทธ์จะแสดงเป็นเปอร์เซ็นต์ และค่าของค่าจะเป็นค่าบวกเสมอ
การตีความค่าเบี่ยงเบนมาตรฐานสัมพัทธ์ใช้เพื่อแสดงการกระจายตัวของตัวอย่างข้อมูล ยิ่งค่าของส่วนเบี่ยงเบนมาตรฐานสัมพัทธ์มากขึ้น ข้อมูลจะกระจัดกระจายมากขึ้น และยิ่งค่าเบี่ยงเบนมาตรฐานสัมพัทธ์น้อยลง ข้อมูลก็ยิ่งเข้าใกล้ค่าเฉลี่ยมากขึ้นเท่านั้น
โดยทั่วไปแล้ว ตัวย่อ RSD จะใช้เป็นสัญลักษณ์ของค่าเบี่ยงเบน มาตรฐาน สัมพัทธ์
สูตรค่าเบี่ยงเบนมาตรฐานสัมพัทธ์
ค่าเบี่ยงเบนมาตรฐานสัมพัทธ์เท่ากับค่าเบี่ยงเบนมาตรฐานหารด้วยค่าเฉลี่ยคูณด้วย 100 ดังนั้น ในการคำนวณค่าเบี่ยงเบนมาตรฐานสัมพัทธ์ คุณต้องหาค่าเบี่ยงเบนมาตรฐานและค่าเฉลี่ยเลขคณิตก่อน จากนั้นจึงหารการวัดทางสถิติทั้งสองค่าแล้วคูณด้วย 100 สุดท้าย
กล่าวอีกนัยหนึ่ง สูตรสำหรับค่าเบี่ยงเบนมาตรฐานสัมพัทธ์ คือ:
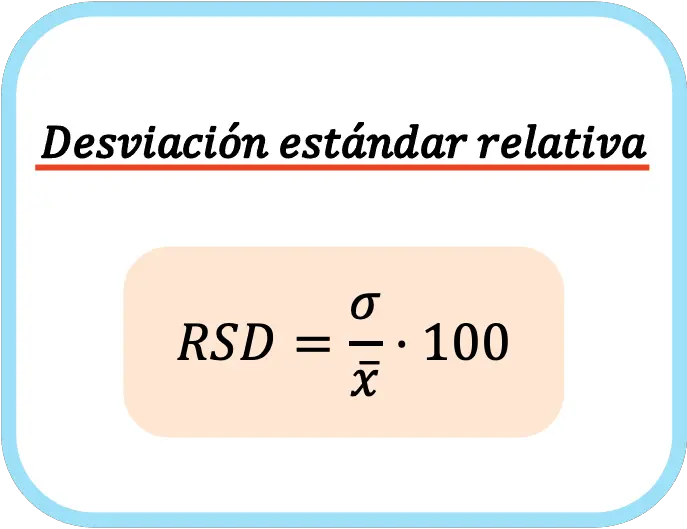
เมื่อคำนวณค่าเบี่ยงเบนมาตรฐานสัมพัทธ์ จะคูณด้วยหนึ่งร้อยเพื่อแสดงค่าเป็นเปอร์เซ็นต์
ตัวอย่างการคำนวณค่าเบี่ยงเบนมาตรฐานสัมพัทธ์
หลังจากทบทวนคำจำกัดความของค่าเบี่ยงเบนมาตรฐานสัมพัทธ์และสูตรของมันแล้ว คุณจะเห็นตัวอย่างที่ชัดเจนของวิธีคำนวณค่าเบี่ยงเบนมาตรฐานสัมพัทธ์ได้ด้านล่างนี้
- คำนวณค่าเบี่ยงเบนมาตรฐานสัมพัทธ์ของชุดข้อมูลทางสถิติต่อไปนี้:
4, 1, 3, 9, 12, 2, 5, 8, 3, 6
ขั้นแรก เราต้องค้นหาค่าเบี่ยงเบนมาตรฐานของข้อมูล:
![]()
ประการที่สอง เราคำนวณค่าเฉลี่ยเลขคณิตของข้อมูล:
![]()
เมื่อเราทราบค่าเบี่ยงเบนมาตรฐานและค่าเฉลี่ยเลขคณิตของชุดข้อมูลแล้ว เราจะใช้สูตรค่าเบี่ยงเบนมาตรฐานแบบสัมพัทธ์
![]()
และสุดท้ายเราแทนที่ค่าที่คำนวณได้ลงในสูตรและคำนวณค่าเบี่ยงเบนมาตรฐานสัมพัทธ์:
![]()