การกระจายแบบไบโมดัลคืออะไร?

การแจกแจงแบบไบโมดัล เป็นการแจกแจงความน่าจะเป็นที่มีสองโหมด

เรามักใช้คำว่า “โหมด” ใน สถิติเชิงพรรณนา เพื่ออ้างถึงค่าที่พบบ่อยที่สุดในชุดข้อมูล แต่ในกรณีนี้ คำว่า “โหมด” หมายถึงค่าสูงสุดเฉพาะจุดในกราฟ

เมื่อดูการกระจายแบบไบโมดัล คุณจะสังเกตเห็น “ยอด” ที่แตกต่างกันสองจุดซึ่งแสดงถึงทั้งสองโหมดนี้

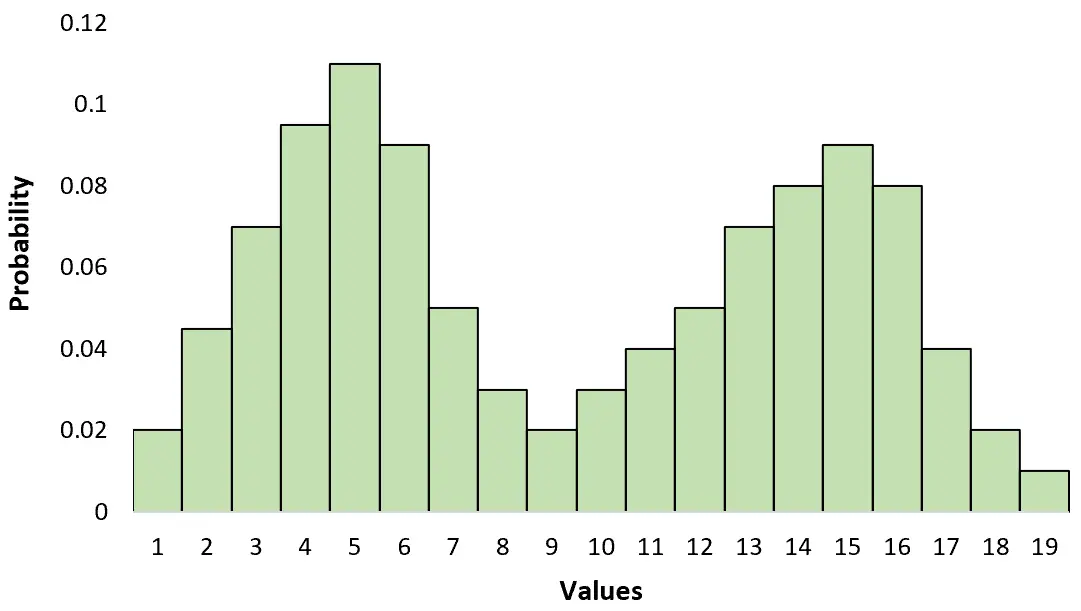
สิ่งนี้แตกต่างจากการแจกแจงแบบ Unimodal ซึ่งมียอดเพียงจุดเดียว:

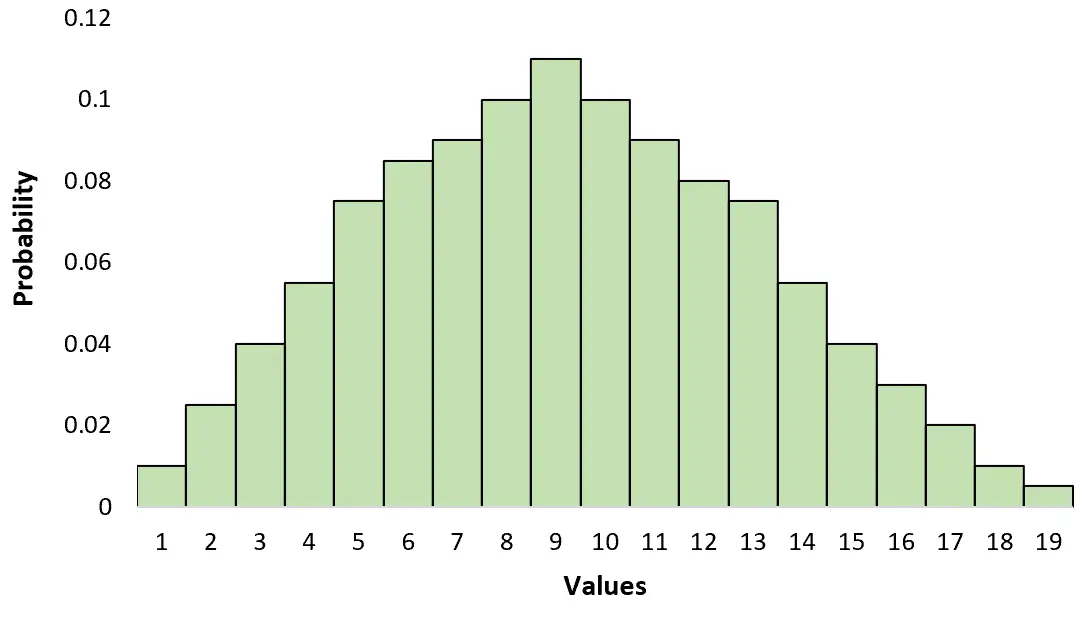
คุณสามารถจำความแตกต่างระหว่างทั้งสองได้โดยการจดจำ:

• “บี” = สอง
• “รวมกัน” = หนึ่ง

แม้ว่าหลักสูตรทางสถิติส่วนใหญ่จะใช้การแจกแจงแบบยูนิโมดัลเช่น การแจกแจงแบบปกติ เพื่ออธิบายหัวข้อต่างๆ แต่ในทางปฏิบัติการแจกแจงแบบไบโมดัลมักปรากฏบ่อยครั้ง ดังนั้นจึงเป็นประโยชน์ที่จะทราบวิธีจดจำและตีความข้อมูลเหล่านั้น

หมายเหตุ: การแจกแจงแบบไบโมดัลเป็นการ แจกแจงแบบมัลติโมดัล ประเภทหนึ่งโดยเฉพาะ

ตัวอย่างของการแจกแจงแบบไบโมดัล

นี่คือตัวอย่างบางส่วนของการแจกแจงแบบไบโมดัล:

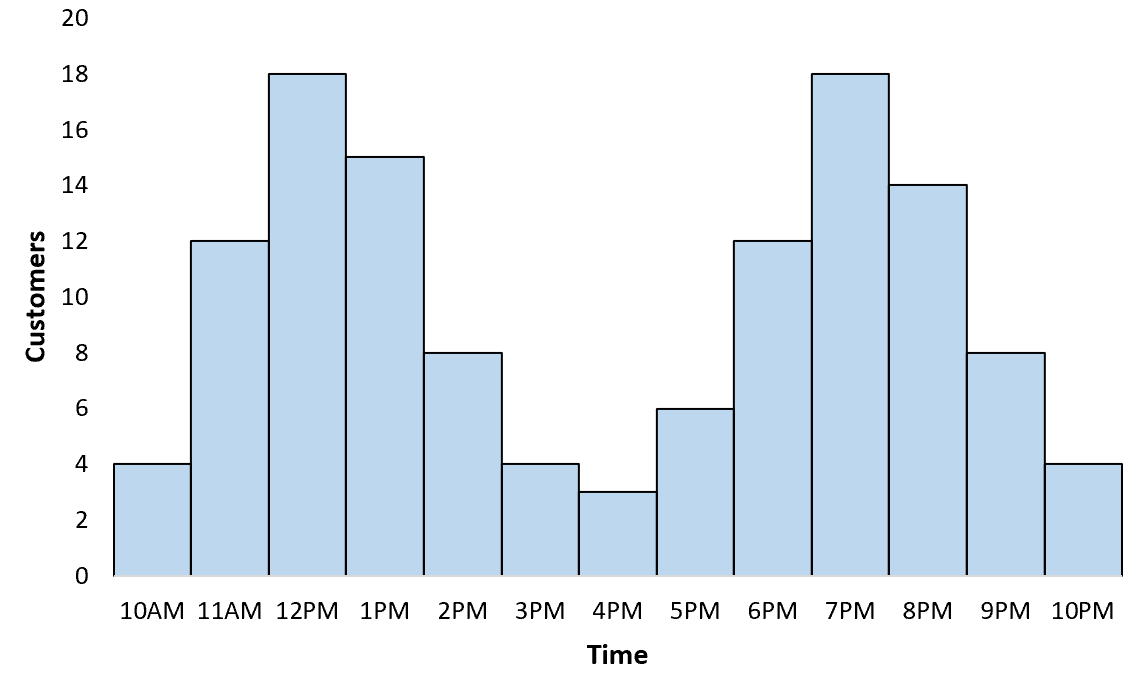
ตัวอย่าง #1: ชั่วโมงเร่งด่วนของร้านอาหาร

หากคุณสร้างกราฟเพื่อแสดงภาพการกระจายตัวของลูกค้ารายชั่วโมงที่ร้านอาหารแห่งหนึ่ง คุณอาจพบว่ากราฟเป็นไปตามการกระจายแบบสองรูปแบบโดยมีจุดสูงสุดในช่วงเวลาอาหารกลางวันและจุดสูงสุดอีกในช่วงเวลาอาหารเย็น:

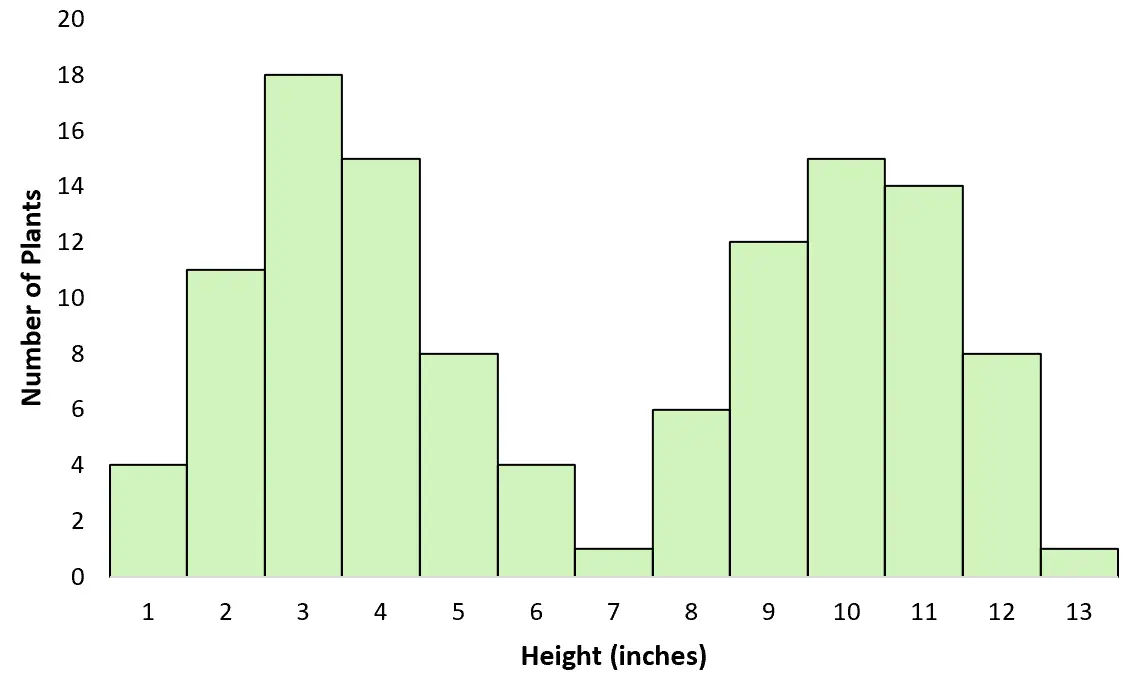
ตัวอย่างหมายเลข 2: ความสูงเฉลี่ยของพืชสองชนิด

สมมติว่าคุณเดินไปรอบๆ ทุ่งนาและวัดความสูงของต้นไม้ต่างๆ คุณกำลังวัดขนาดของสองสายพันธุ์ที่แตกต่างกัน โดยที่ไม่รู้ตัว สายพันธุ์หนึ่งค่อนข้างใหญ่ และอีกสายพันธุ์ค่อนข้างเล็ก หากคุณสร้างกราฟเพื่อแสดงภาพการกระจายตัวของความสูง กราฟนั้นจะเป็นไปตามการกระจายแบบสองโมดัล:

ตัวอย่างที่ 3: ผลการสอบ

สมมติว่าครูทำข้อสอบให้นักเรียนในชั้นเรียนของเขา นักเรียนบางคนเรียนเพื่อสอบ ส่วนคนอื่นๆ ไม่ได้เรียน เมื่อครูสร้างกราฟผลการสอบ จะเป็นไปตามการแจกแจงแบบสองรูปแบบโดยมีจุดสูงสุดประมาณคะแนนต่ำสำหรับนักเรียนที่ไม่ได้เรียน และอีกจุดสูงสุดเกี่ยวกับคะแนนสูงสำหรับนักเรียนที่เรียน:

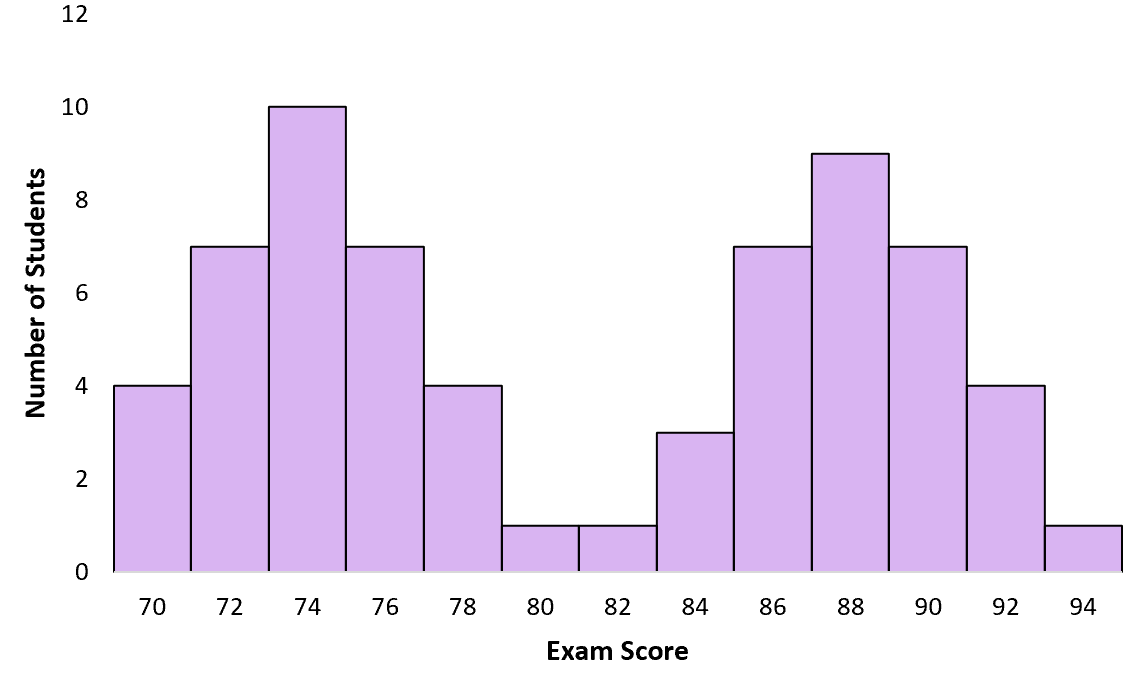
อะไรทำให้เกิดการแจกแจงแบบไบโมดัล?

โดยทั่วไปมีสองสิ่งที่ทำให้เกิดการแจกแจงแบบไบโมดัล:

1. ปรากฏการณ์ที่ซ่อนอยู่บางประการ

การแจกแจงแบบไบโมดัลมักเกิดขึ้นเนื่องจากปรากฏการณ์พื้นฐานบางประการ

ตัวอย่างเช่น จำนวนลูกค้าที่มาร้านอาหารในแต่ละชั่วโมงเป็นไปตามการกระจายแบบสองรูปแบบ เนื่องจากผู้คนมักจะรับประทานอาหารที่ร้านอาหารในเวลาที่แตกต่างกันสองเวลา คือ มื้อกลางวันและมื้อเย็น พฤติกรรมของมนุษย์ที่ซ่อนอยู่นี้เป็นที่มาของการกระจายแบบไบโมดัล

2. สองกลุ่มที่แตกต่างกันจัดกลุ่มเข้าด้วยกัน

การแจกแจงแบบไบโมดัลยังสามารถเกิดขึ้นได้เมื่อคุณวิเคราะห์กลุ่มสิ่งต่าง ๆ สองกลุ่มโดยที่ไม่รู้ตัว

ตัวอย่างเช่น หากคุณวัดความสูงของต้นไม้ในพื้นที่ใดพื้นที่หนึ่งโดยไม่รู้ว่ามี 2 สายพันธุ์ที่แตกต่างกันเติบโตในพื้นที่เดียวกัน คุณจะเห็นการกระจายแบบสองรูปแบบเมื่อคุณสร้างกราฟ

วิธีการวิเคราะห์การแจกแจงแบบไบโมดัล

เรามักจะอธิบายการแจกแจงโดยใช้ ค่าเฉลี่ยหรือค่ามัธยฐาน เพราะมันช่วยให้เราทราบว่า “ศูนย์กลาง” ของการแจกแจงอยู่ที่ไหน

น่าเสียดายที่ค่าเฉลี่ยและค่ามัธยฐานไม่มีประโยชน์ที่จะรู้สำหรับการแจกแจงแบบไบโมดัล ตัวอย่างเช่น คะแนนสอบเฉลี่ยของนักเรียนตามตัวอย่างข้างต้นคือ 81:

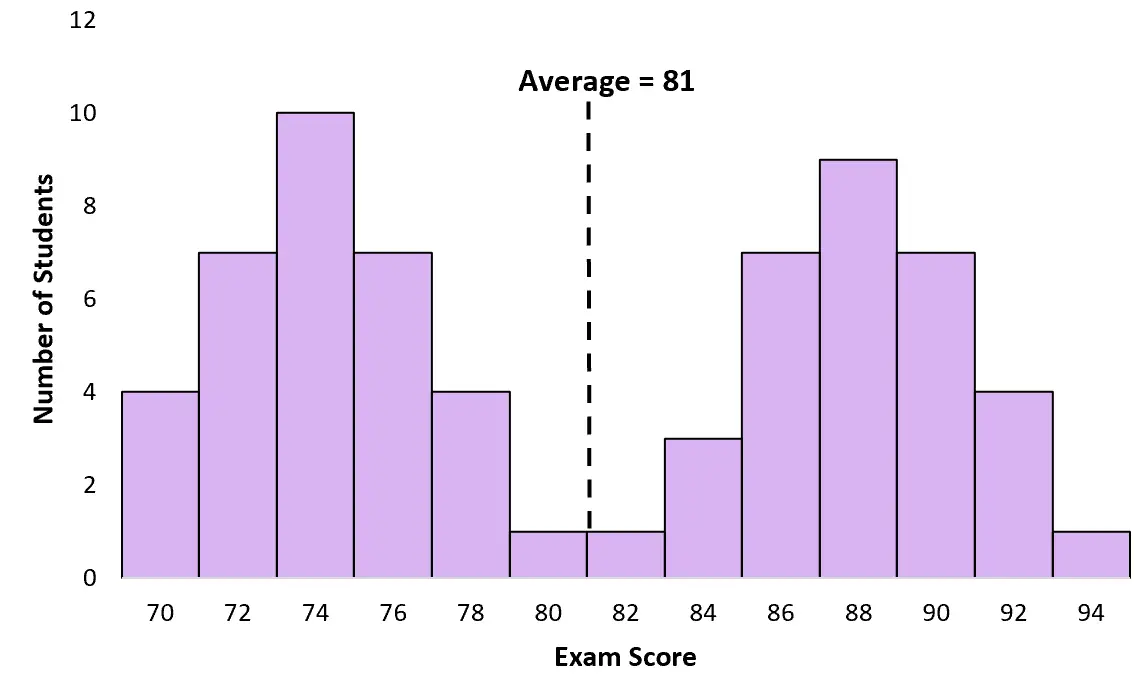
อย่างไรก็ตาม มีนักเรียนเพียงไม่กี่คนที่ทำคะแนนได้ใกล้ 81 ในกรณีนี้ ค่าเฉลี่ยอาจทำให้เข้าใจผิด นักเรียนส่วนใหญ่ได้คะแนนจริงประมาณ 74 หรือ 88

วิธีที่ดีกว่าในการวิเคราะห์และตีความการแจกแจงแบบไบโมดัลคือการแบ่งข้อมูลออกเป็นสองกลุ่ม จากนั้นวิเคราะห์ศูนย์กลางและการกระจายสำหรับแต่ละกลุ่ม

เช่น เราสามารถแบ่งผลการสอบเป็น “คะแนนต่ำ” และ “คะแนนสูง” แล้วหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของแต่ละกลุ่ม

หากคุณกำลังแบ่งปันผลลัพธ์ของการวิเคราะห์และข้อมูลของคุณเป็นไปตามการแจกแจงแบบไบโมดัล การสร้างฮิสโตแกรมเหมือนกับที่แสดงไว้ด้านบนจะเป็นประโยชน์ เพื่อให้ผู้ชมของคุณมองเห็นได้อย่างชัดเจนว่าการแจกแจงนั้นมี “จุดสูงสุด” สองจุดที่แตกต่างกัน และเพียงทำให้ สมเหตุสมผลที่จะวิเคราะห์แต่ละจุดสูงสุดแยกกัน แทนที่จะเป็นชุดข้อมูลขนาดใหญ่ชุดเดียว