วิธีสร้างเมทริกซ์สหสัมพันธ์ใน python

วิธีหนึ่งในการหาปริมาณความสัมพันธ์ระหว่างตัวแปรสองตัวคือการใช้ สัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน ซึ่ง เป็นหน่วยวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว

ใช้ค่าระหว่าง -1 ถึง 1 โดยที่:

• -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์
• 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้น
• 1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์

ยิ่งค่าสัมประสิทธิ์สหสัมพันธ์จากศูนย์มากเท่าใด ความสัมพันธ์ระหว่างตัวแปรทั้งสองก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น

แต่ในบางกรณี เราต้องการเข้าใจความสัมพันธ์ระหว่างตัวแปรหลายคู่ ในกรณีเหล่านี้ เราสามารถสร้าง เมทริกซ์สหสัมพันธ์ ซึ่งเป็นตารางสี่เหลี่ยมที่แสดงค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างการผสมตัวแปรหลายคู่ตามลำดับ

บทช่วยสอนนี้จะอธิบายวิธีสร้างและตีความเมทริกซ์สหสัมพันธ์ใน Python

วิธีสร้างเมทริกซ์สหสัมพันธ์ใน Python

ใช้ขั้นตอนต่อไปนี้เพื่อสร้างเมทริกซ์สหสัมพันธ์ใน Python

ขั้นตอนที่ 1: สร้างชุดข้อมูล

 import pandas as pd

data = {'assists': [4, 5, 5, 6, 7, 8, 8, 10],
        'rebounds': [12, 14, 13, 7, 8, 8, 9, 13],
        'points': [22, 24, 26, 26, 29, 32, 20, 14]
        }

df = pd. DataFrame (data, columns=['assists','rebounds','points'])
df

   assist rebound points
0 4 12 22
1 5 14 24
2 5 13 26
3 6 7 26
4 7 8 29
5 8 8 32
6 8 9 20
7 10 13 14

ขั้นตอนที่ 2: สร้างเมทริกซ์สหสัมพันธ์

 #create correlation matrix
df. corr ()

                assists rebound points
assists 1.000000 -0.244861 -0.329573
rebounds -0.244861 1.000000 -0.522092
points -0.329573 -0.522092 1.000000

#create same correlation matrix with coefficients rounded to 3 decimals 
df. corr (). round (3)
	       assists rebound points
assists 1.000 -0.245 -0.330
rebounds -0.245 1.000 -0.522
points -0.330 -0.522 1.000

ขั้นตอนที่ 3: ตีความเมทริกซ์สหสัมพันธ์

ค่าสัมประสิทธิ์สหสัมพันธ์ตามเส้นทแยงมุมของตารางมีค่าเท่ากับ 1 เนื่องจากตัวแปรแต่ละตัวมีความสัมพันธ์อย่างสมบูรณ์กับตัวมันเอง

ค่าสัมประสิทธิ์สหสัมพันธ์อื่นๆ ทั้งหมดบ่งบอกถึงความสัมพันธ์ระหว่างการรวมตัวแปรแบบคู่ต่างๆ ตัวอย่างเช่น:

• ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างการแอสซิสต์และการรีบาวด์คือ -0.245
• ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างแอสซิสต์และแต้มคือ -0.330
• ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างการรีบาวด์และคะแนนคือ -0.522

ขั้นตอนที่ 4: แสดงภาพเมทริกซ์สหสัมพันธ์ (ไม่บังคับ)

คุณสามารถเห็นภาพเมทริกซ์สหสัมพันธ์ได้โดยใช้ ตัวเลือกสไตล์ ที่มีอยู่ในแพนด้า:

 corr = df. corr ()
corr. style . background_gradient (cmap='coolwarm')

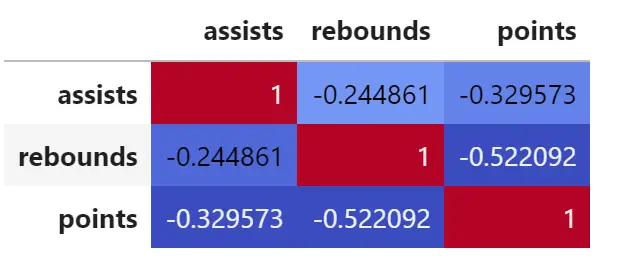
คุณยังสามารถแก้ไขอาร์กิวเมนต์ cmap เพื่อสร้างเมทริกซ์สหสัมพันธ์ที่มีสีต่างกันได้

 corr = df. corr ()
corr. style . background_gradient (cmap=' RdYlGn ') 

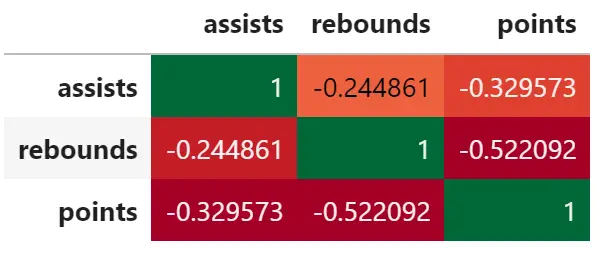
 corr = df. corr ()
corr. style . background_gradient (cmap=' bwr ') 

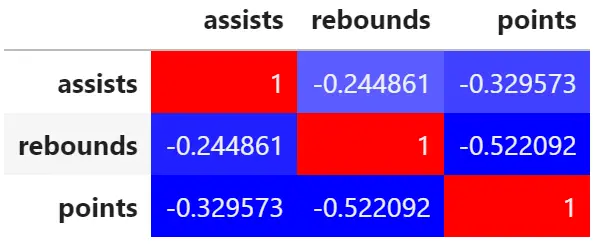
 corr = df. corr ()
corr. style . background_gradient (cmap=' PuOr ') 

หมายเหตุ : สำหรับรายการอาร์กิวเมนต์ Cmap ทั้งหมด โปรดดู เอกสารประกอบของ matplotlib