ค่ามัธยฐาน
บทความนี้จะอธิบายว่าค่ามัธยฐานของชุดข้อมูลคืออะไร และวิธีค้นหาค่ามัธยฐานของข้อมูลที่ไม่ได้จัดกลุ่มและข้อมูลที่จัดกลุ่ม นอกจากนี้ คุณยังสามารถคำนวณค่ามัธยฐานของชุดข้อมูลใดๆ ได้ด้วยเครื่องคิดเลขออนไลน์ในตอนท้าย
ค่ามัธยฐานคืออะไร?
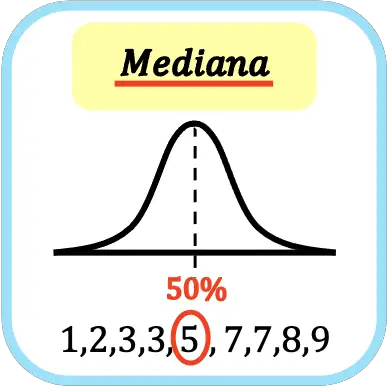
ในทางสถิติ ค่ามัธยฐาน คือค่ากลางของข้อมูลทั้งหมดโดยเรียงลำดับจากน้อยไปหามาก กล่าวอีกนัยหนึ่ง ค่ามัธยฐานจะแบ่งชุดข้อมูลที่เรียงลำดับออกเป็นสองส่วนเท่าๆ กัน
ค่ามัธยฐานคือการวัดตำแหน่งศูนย์กลางที่ใช้อธิบายการแจกแจงความน่าจะเป็น
👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่ามัธยฐานของชุดข้อมูลใดก็ได้
โดยทั่วไปแล้วคำว่า ตนเอง มักจะใช้เป็นสัญลักษณ์ของคนตรงกลาง
การวัดตำแหน่งศูนย์กลางอื่นๆ คือค่าเฉลี่ยและโหมด ด้านล่างนี้เราจะเห็นความแตกต่างระหว่างสิ่งเหล่านั้น ในทำนองเดียวกัน การวัดตำแหน่งที่ไม่อยู่ตรงกลาง ได้แก่ ควอร์ไทล์ ควินไทล์ เดซิล เปอร์เซ็นไทล์ เป็นต้น
ควรสังเกตว่าค่ามัธยฐานของชุดข้อมูลเกิดขึ้นพร้อมกับควอร์ไทล์ที่ 2 เดซิล์ที่ 5 และเปอร์เซ็นไทล์ที่ 50
วิธีการคำนวณค่ามัธยฐาน
การคำนวณค่ามัธยฐานขึ้นอยู่กับว่าจำนวนข้อมูลทั้งหมดเป็นเลขคู่หรือคี่:
- หากจำนวนข้อมูลทั้งหมดเป็นเลข คี่ ค่ามัธยฐานจะเป็นค่าที่อยู่ตรงกลางข้อมูล กล่าวคือค่าที่อยู่ในตำแหน่ง (n+1)/2 ของข้อมูลที่เรียงลำดับ
- หากจำนวนจุดข้อมูลทั้งหมดเป็น เลขคู่ ค่ามัธยฐานจะเป็นค่าเฉลี่ยของจุดข้อมูล 2 จุดที่อยู่ตรงกลาง กล่าวคือ ค่าเฉลี่ยเลขคณิต ของค่าที่พบในตำแหน่ง n/2 และ n/2+1 ของข้อมูลที่เรียงลำดับ
![]()
![]()
ทอง
![]()
คือจำนวนรายการข้อมูลทั้งหมดในกลุ่มตัวอย่าง
ตัวอย่างการคำนวณค่ามัธยฐาน
เพื่อให้คุณสามารถดูวิธีการคำนวณค่ามัธยฐาน ด้านล่างนี้คือตัวอย่างจากโลกแห่งความเป็นจริงสองตัวอย่าง สำหรับแต่ละกรณี ขั้นแรก ค่ามัธยฐานของชุดข้อมูลคี่จะถูกคำนวณ จากนั้นค่ามัธยฐานจะถูกคำนวณด้วยชุดข้อมูลเลขคู่
ค่ามัธยฐานของข้อมูลคี่
- คำนวณค่ามัธยฐานของข้อมูลต่อไปนี้: 3, 4, 1, 6, 7, 4, 8, 2, 8, 4, 5
สิ่งแรกที่เราต้องทำก่อนทำการคำนวณคือการเรียงลำดับข้อมูล นั่นคือ เราใส่ตัวเลขจากน้อยไปหามาก
![]()
ในกรณีนี้ เรามีข้อสังเกต 11 รายการ ดังนั้นจำนวนข้อมูลทั้งหมดจึงเป็นเลขคี่ ดังนั้นเราจึงใช้สูตรต่อไปนี้เพื่อคำนวณตำแหน่งของค่ามัธยฐาน:
![]()
ค่ามัธยฐานจึงเป็นข้อมูลที่อยู่ในตำแหน่งที่ 6 ซึ่งในกรณีนี้จะสอดคล้องกับค่า 4
![]()
ค่ามัธยฐานของข้อมูลคู่
- ค่ามัธยฐานของการสังเกตต่อไปนี้คือข้อใด 2, 6, 2, 8, 9, 4, 7, 11, 4, 13
หากต้องการหาค่ามัธยฐาน คุณต้องเรียงลำดับข้อมูลทั้งหมดจากน้อยไปหามากก่อน:
![]()
ตัวอย่างนี้แตกต่างจากตัวอย่างก่อนหน้า เนื่องจากครั้งนี้เรามีข้อสังเกตทั้งหมด 10 รายการ ซึ่งเป็นจำนวนคู่ ดังนั้นขั้นตอนการกำหนดค่าเฉลี่ยจึงซับซ้อนกว่าเล็กน้อย
ก่อนอื่นคุณต้องคำนวณตำแหน่งศูนย์กลางสองตำแหน่งที่จะหาค่ามัธยฐานได้ ซึ่งคุณจะต้องใช้สูตรสองสูตรต่อไปนี้:
![]()
![]()
ค่ามัธยฐานจะอยู่ระหว่างตำแหน่งที่ห้าและหกซึ่งสอดคล้องกับค่า 6 และ 7 ตามลำดับ โดยสรุปแล้ว ค่ามัธยฐานจะเป็นค่าเฉลี่ยเลขคณิตของค่าดังกล่าว:
![]()
เครื่องคิดเลขค่ามัธยฐาน
ป้อนข้อมูลทางสถิติลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณค่ามัธยฐาน ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม
ค่ามัธยฐานสำหรับข้อมูลที่จัดกลุ่ม
ในการ คำนวณค่ามัธยฐานเมื่อข้อมูลถูกจัดกลุ่มตามช่วงเวลา คุณต้องค้นหาช่วงเวลาหรือช่องเก็บที่ค่ามัธยฐานตกอยู่ก่อนโดยใช้สูตรต่อไปนี้:
![]()
ดังนั้นค่ามัธยฐานจะอยู่ในช่วงที่ความถี่สัมบูรณ์สะสมมากกว่าจำนวนที่ได้รับจากนิพจน์พีชคณิตก่อนหน้าทันที
และเมื่อเรารู้ช่วงที่เป็นค่ามัธยฐานแล้ว เราต้องใช้สูตรต่อไปนี้เพื่อค้นหาค่ามัธยฐานที่แน่นอน:

ทอง:
- L i คือขีดจำกัดล่างของช่วงเวลาที่ค่ามัธยฐานอยู่
- n คือจำนวนการสังเกตทั้งหมด
- F i-1 คือความถี่สัมบูรณ์สะสมของช่วงก่อนหน้า
- f i คือความถี่สัมบูรณ์ของช่วงเวลาที่ค่ามัธยฐานอยู่
- ฉัน คือความกว้างของช่วงกลาง
ตามตัวอย่าง ด้านล่างคุณได้แก้แบบฝึกหัดที่คำนวณค่ามัธยฐานของข้อมูลที่จัดกลุ่มตามช่วงเวลา

ในการค้นหาค่ามัธยฐานของชุดข้อมูล เราต้องกำหนดช่วงที่ข้อมูลตกก่อน เมื่อต้องการทำเช่นนี้ เราใช้สูตรต่อไปนี้:
![]()
ค่ามัธยฐานจะอยู่ในช่วงที่ความถี่สัมบูรณ์สะสมมากกว่า 15.5 ทันที ซึ่งในกรณีนี้คือช่วง [60.70) ซึ่งมีความถี่สัมบูรณ์สะสมเท่ากับ 26 และเมื่อเรารู้ช่วงค่ามัธยฐานแล้ว เราก็ใช้สูตรที่สองของ กระบวนการ:


ท้ายที่สุดแล้ว ค่ามัธยฐานของชุดข้อมูลที่รวมกลุ่มคือ 60.45 อย่างที่คุณเห็น ในปัญหาประเภทนี้ ค่ามัธยฐานมักจะเป็นเลขทศนิยม
ค่ามัธยฐานค่าเฉลี่ยและโหมด
ในส่วนสุดท้ายนี้ เราจะดูว่าอะไรคือความแตกต่างระหว่างค่ามัธยฐาน ค่าเฉลี่ย และโหมด นี่เป็นการวัดทางสถิติสามประการของตำแหน่งศูนย์กลาง แต่ความหมายของมันต่างกัน
ดังที่เราได้เห็นไปแล้ว ค่ามัธยฐานถูกกำหนดให้เป็นค่าที่ครองตำแหน่งศูนย์กลางเมื่อมีการเรียงลำดับข้อมูล
ในทางตรงกันข้าม ค่าเฉลี่ยคือค่าเฉลี่ยของข้อมูลทางสถิติทั้งหมด ในการคำนวณค่าเฉลี่ย คุณต้องเพิ่มข้อมูลทั้งหมดแล้วหารผลลัพธ์ด้วยจำนวนจุดข้อมูล
สุดท้าย โหมดนี้จะเป็นค่าที่ซ้ำกันมากที่สุดในชุดข้อมูล
อย่างที่คุณเห็น มาตรการทางสถิติทั้งสามช่วยอธิบายการแจกแจงความน่าจะเป็น เนื่องจากมาตรการเหล่านี้ให้แนวคิดเกี่ยวกับค่ากลางของมัน อย่างไรก็ตาม ไม่มีการวัดผลใดที่ดีไปกว่าการวัดอื่น เพียงแต่อ้างอิงถึงแนวคิดที่แตกต่างกัน