ทำความเข้าใจรูปร่างของการแจกแจงแบบทวินาม

การแจกแจงแบบทวินาม อธิบายถึงความน่าจะเป็นที่จะประสบความสำเร็จ k ครั้งในการทดลองทวินาม n ครั้ง

หาก ตัวแปรสุ่ม X เป็นไปตามการแจกแจงแบบทวินาม ความน่าจะเป็นที่ X = k สำเร็จจะพบได้จากสูตรต่อไปนี้:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

ทอง:

• n: จำนวนการทดลอง
• k: จำนวนความสำเร็จ
• p: ความน่าจะเป็นที่จะประสบความสำเร็จในการทดลองที่กำหนด
• _n C _k : จำนวนวิธีในการได้รับ k ความสำเร็จในการทดลอง n ครั้ง

การแจกแจงความน่าจะเป็นแบบทวินามมีแนวโน้มที่จะเป็นรูประฆังเมื่อมีเงื่อนไขหนึ่งหรือหลายข้อต่อไปนี้เกิดขึ้น:

1. ขนาดตัวอย่าง (n) มีขนาดใหญ่

2. ความน่าจะเป็นที่จะประสบความสำเร็จสำหรับการทดลองที่กำหนด (p) อยู่ใกล้กับ 0.5

อย่างไรก็ตาม การแจกแจงความน่าจะเป็นแบบทวินามมีแนวโน้มที่จะบิดเบือนเมื่อไม่มีเงื่อนไขใดเกิดขึ้น เพื่ออธิบายสิ่งนี้ ให้พิจารณาตัวอย่างต่อไปนี้:

ตัวอย่างที่ 1: ขนาดตัวอย่าง (n) มีขนาดใหญ่

กราฟต่อไปนี้แสดงการแจกแจงความน่าจะเป็นเมื่อ n = 200 และ p = 0.5

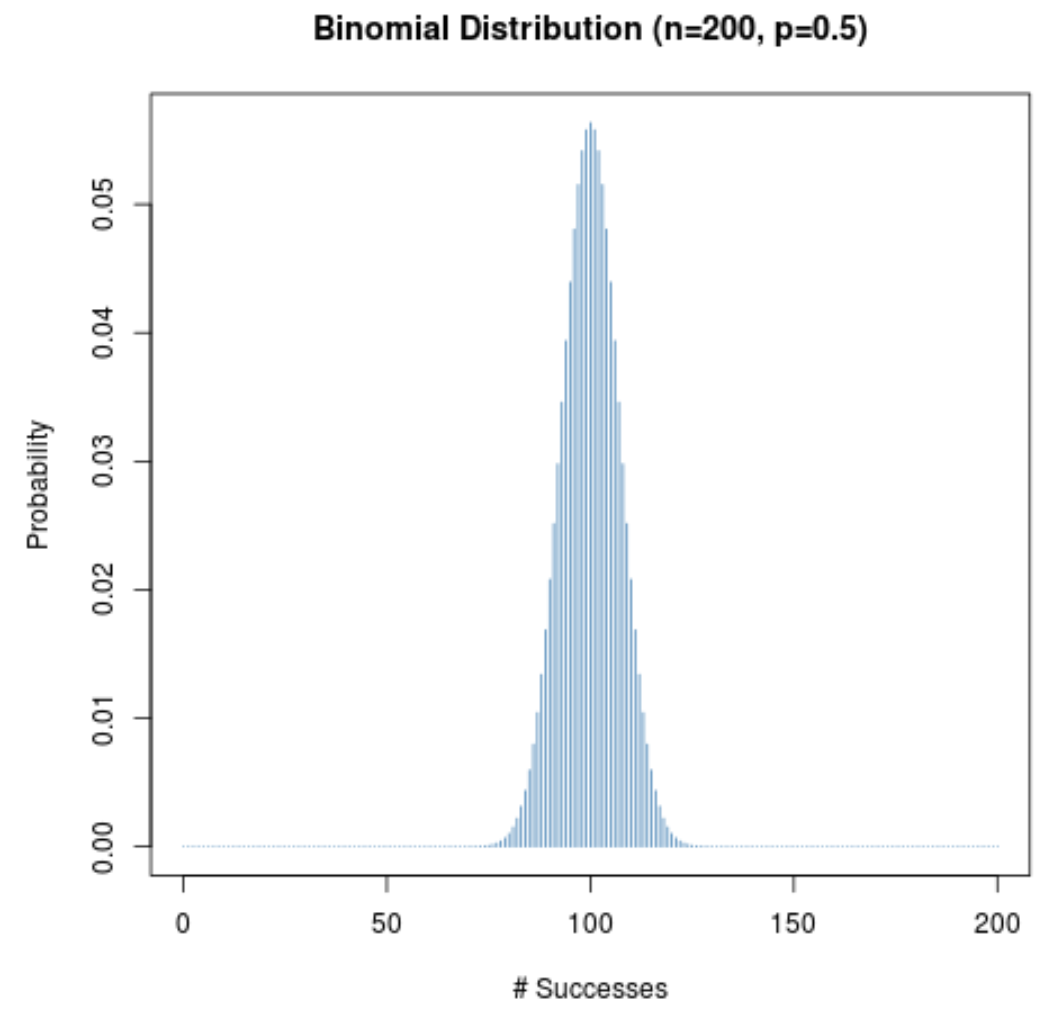
แกน x จะแสดงจำนวนความสำเร็จในการทดลอง 200 ครั้ง และแกน y แสดงความน่าจะเป็นของจำนวนความสำเร็จที่เกิดขึ้น

เนื่องจาก (1) ขนาดกลุ่มตัวอย่างมีขนาดใหญ่ และ (2) ความน่าจะเป็นที่จะประสบความสำเร็จสำหรับการทดลองที่กำหนดนั้นอยู่ใกล้กับ 0.5 การกระจายความน่าจะเป็นจึงเป็นรูประฆัง

แม้ว่าความน่าจะเป็นที่จะประสบความสำเร็จสำหรับการทดลองที่กำหนด (p) จะไม่ใกล้เคียงกับ 0.5 การกระจายความน่าจะเป็นจะยังคงเป็นรูประฆังตราบใดที่ขนาดตัวอย่าง (n) มีขนาดใหญ่ เพื่ออธิบายสิ่งนี้ ให้พิจารณาสองสถานการณ์ต่อไปนี้เมื่อ p = 0.2 และ p = 0.8

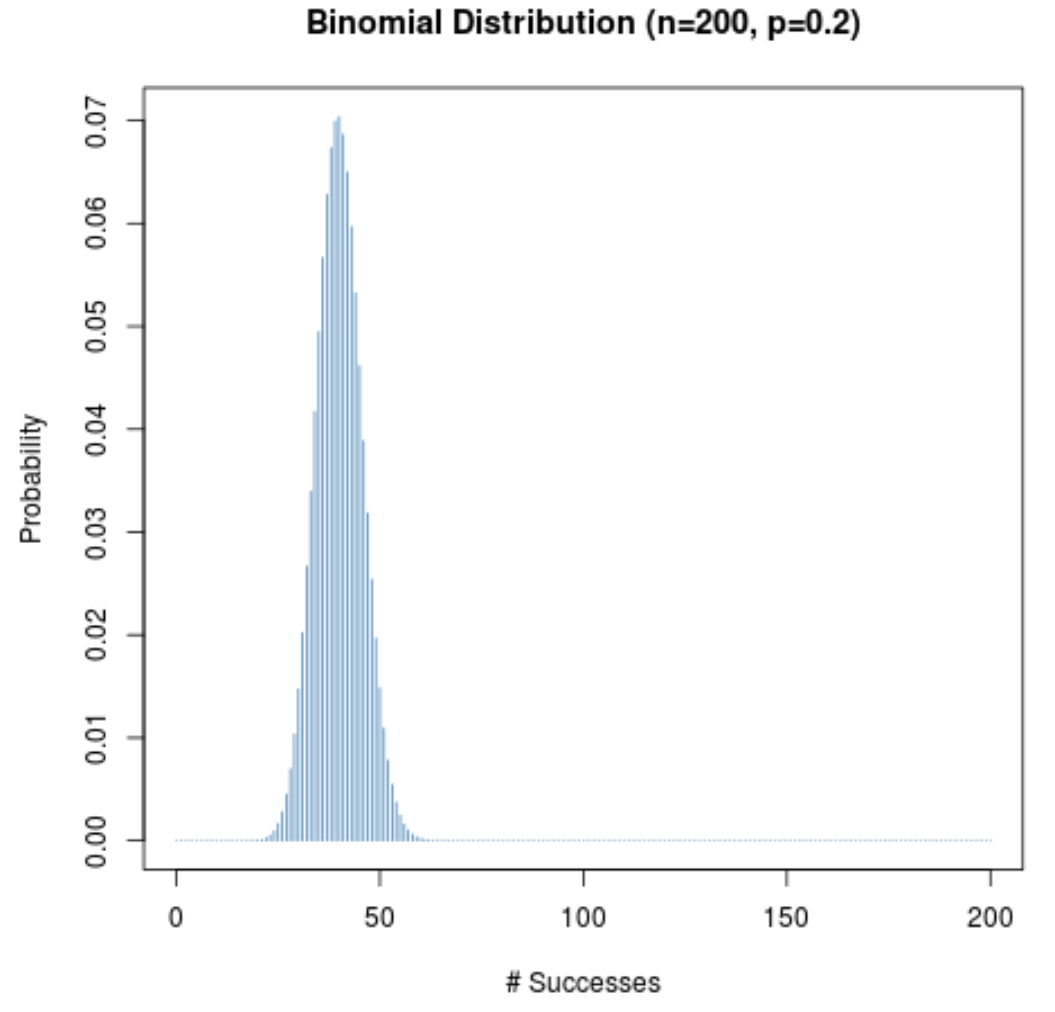
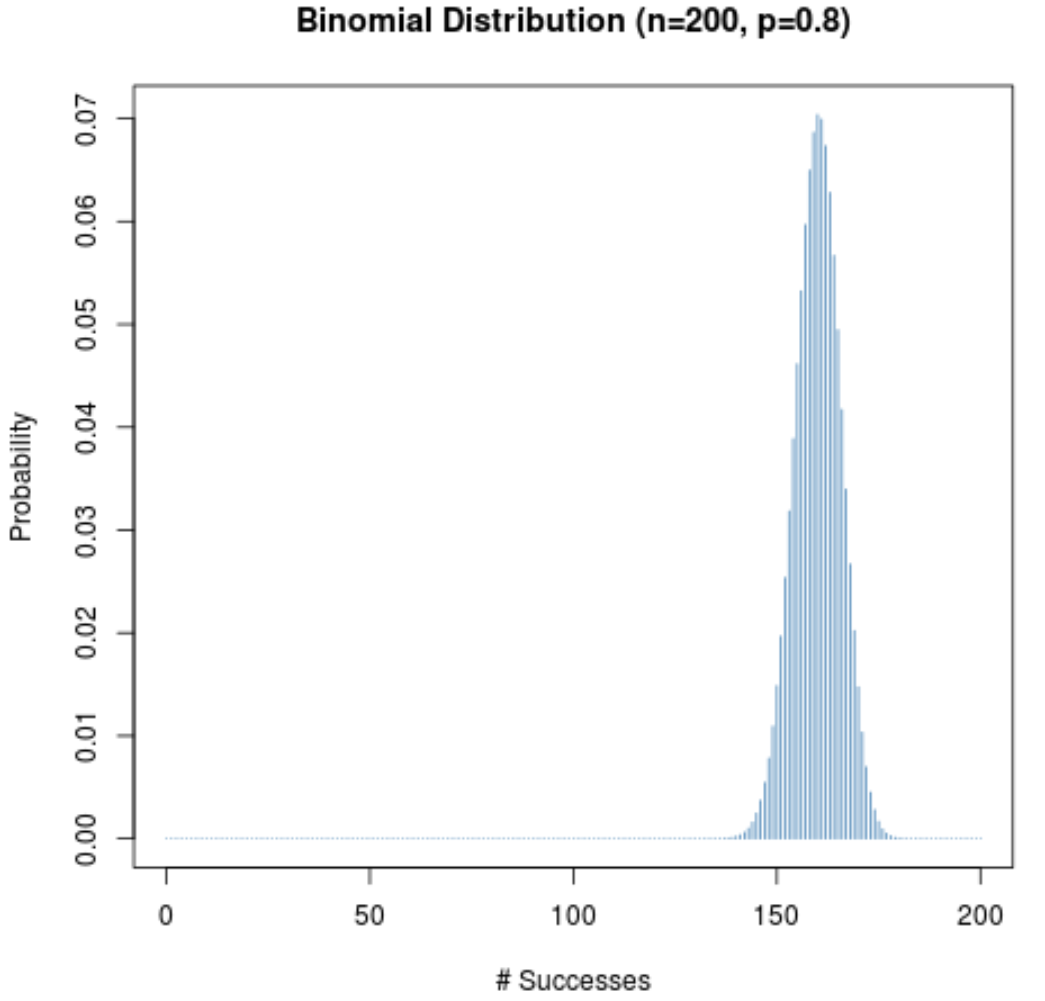
สังเกตว่าการแจกแจงความน่าจะเป็นเป็นรูประฆังในทั้งสองสถานการณ์อย่างไร

ตัวอย่างที่ 2: ความน่าจะเป็นที่จะสำเร็จ (p) ใกล้ถึง 0.5

กราฟต่อไปนี้แสดงการแจกแจงความน่าจะเป็นเมื่อ n = 10 และ p = 0.4

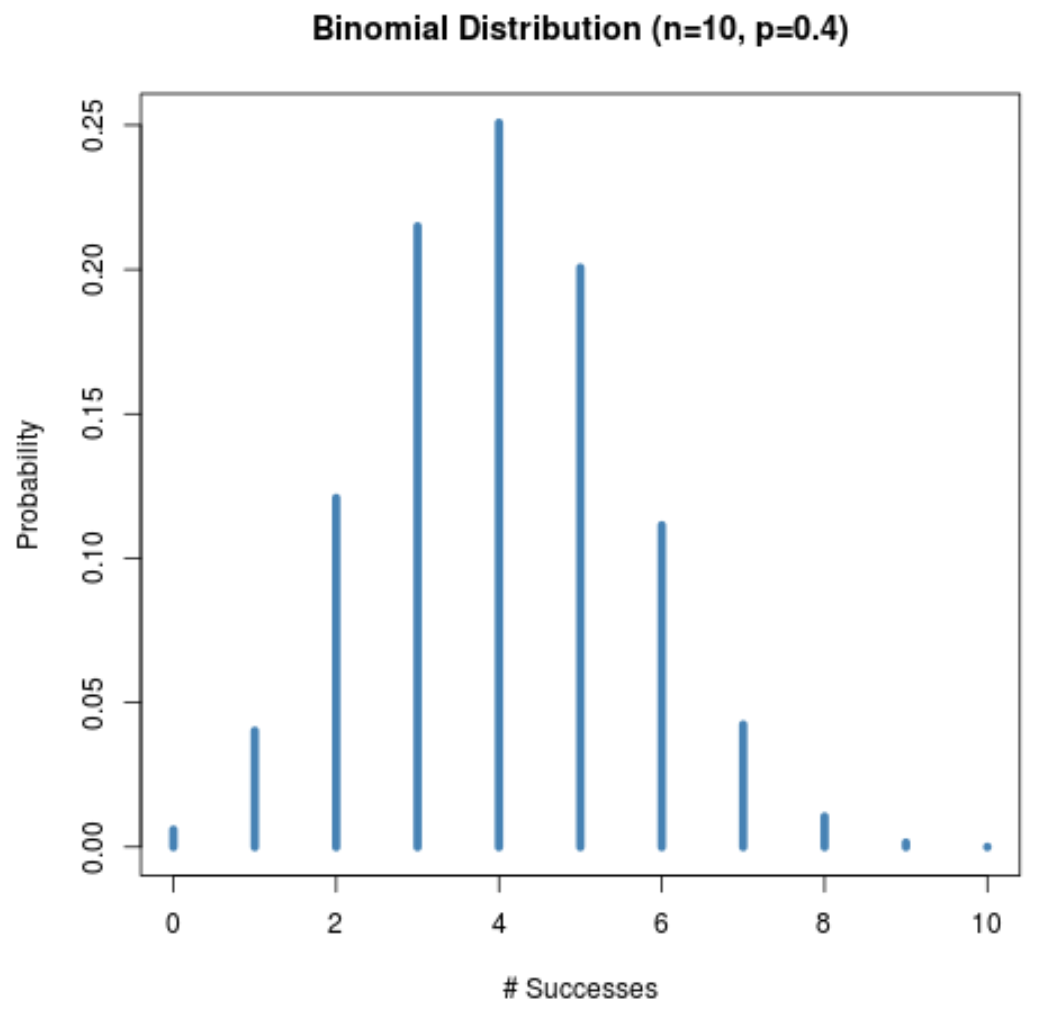
แม้ว่าขนาดกลุ่มตัวอย่าง (n = 10) จะน้อย แต่การแจกแจงความน่าจะเป็นยังคงเป็นรูประฆัง เนื่องจากความน่าจะเป็นที่จะประสบความสำเร็จสำหรับการทดลองที่กำหนด (p = 0.4) อยู่ใกล้กับ 0.5

ตัวอย่างที่ 3: การแจกแจงทวินามแบบเบ้

เมื่อ (1) ขนาดตัวอย่างไม่ใหญ่ และ (2) ความน่าจะเป็นที่จะประสบความสำเร็จของการทดลองใด ๆ ก็ไม่ใกล้เคียงกับ 0.5 การแจกแจงความน่าจะเป็นแบบทวินามจะเบ้ไปทางซ้ายหรือขวา

ตัวอย่างเช่น กราฟต่อไปนี้แสดงการแจกแจงความน่าจะเป็นเมื่อ n = 20 และ p = 0.1

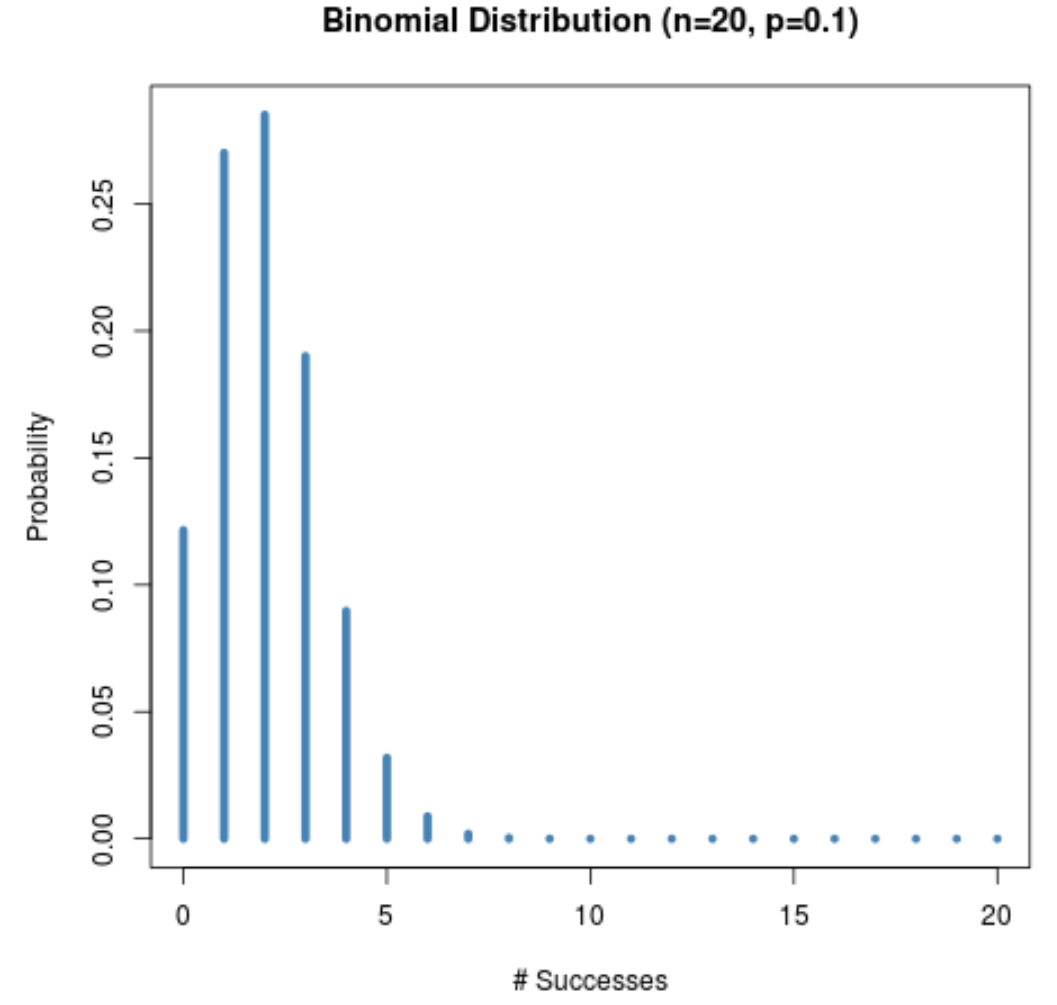
สังเกตว่าการกระจายตัวเอียงไปทางขวาอย่างไร

และกราฟต่อไปนี้แสดงการแจกแจงความน่าจะเป็นเมื่อ n = 20 และ p = 0.9

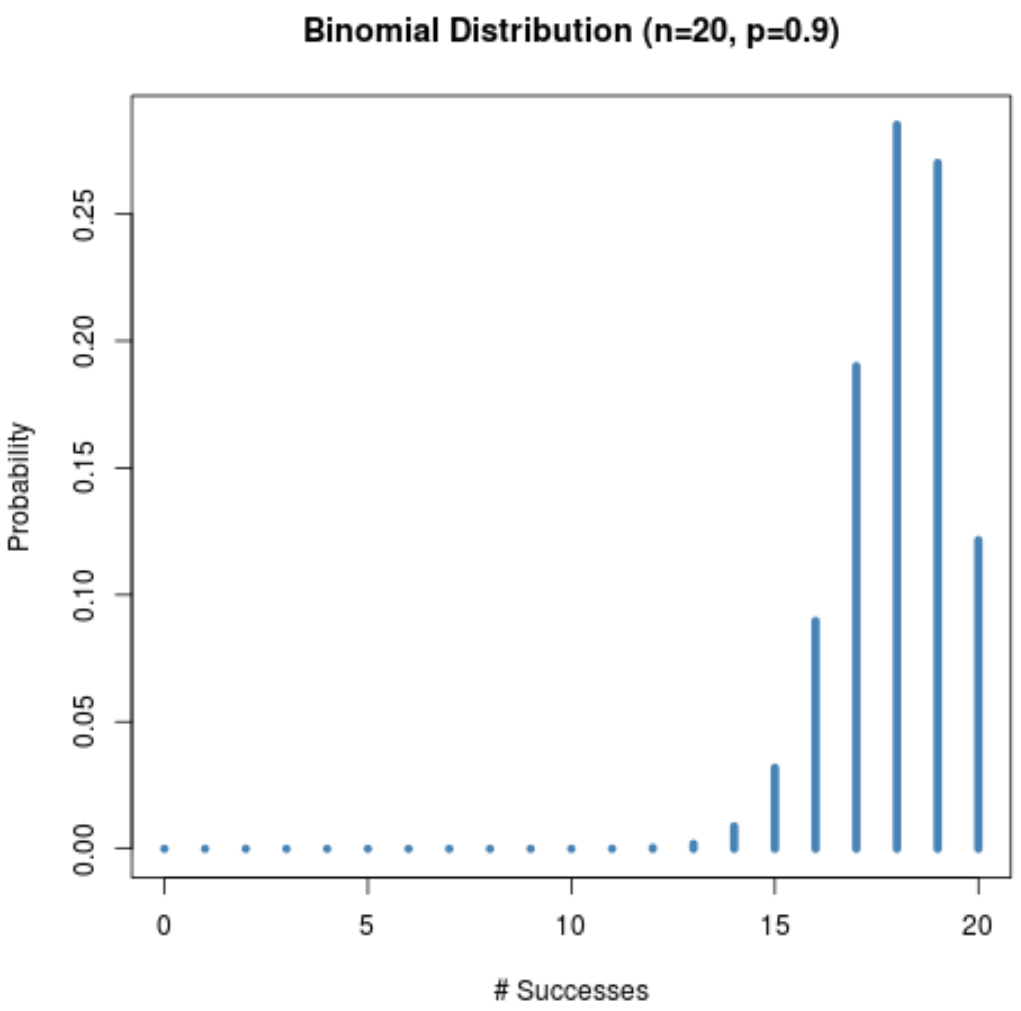
สังเกตว่าการกระจายตัวเอียงไปทางซ้ายอย่างไร

อ้างอิงท้ายเรื่อง

กราฟแต่ละกราฟในบทความนี้สร้างขึ้นโดยใช้ภาษาการเขียนโปรแกรมเชิงสถิติ R เรียนรู้วิธีพล็อตการแจกแจงความน่าจะเป็นแบบทวินามของคุณเองใน R โดยใช้ บทช่วยสอนนี้