วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน excel

การวิเคราะห์ ความแปรปรวนแบบสองทาง (“การวิเคราะห์ความแปรปรวน”) ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปที่ถูกแบ่งออกเป็นสองปัจจัยหรือไม่

บทช่วยสอนนี้จะอธิบายวิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน Excel

ตัวอย่าง: การวิเคราะห์ความแปรปรวนแบบสองทางใน Excel

นักพฤกษศาสตร์ต้องการทราบว่าการเจริญเติบโตของพืชได้รับอิทธิพลจากการสัมผัสกับแสงแดดและความถี่ในการรดน้ำหรือไม่ เธอปลูกเมล็ดพืช 40 เมล็ดและปล่อยให้มันเติบโตเป็นเวลาสองเดือนในสภาพแสงแดดและความถี่ในการรดน้ำที่แตกต่างกัน หลังจากผ่านไปสองเดือน เธอก็บันทึกความสูงของต้นไม้แต่ละต้น ผลลัพธ์แสดงไว้ด้านล่าง:

ในตารางด้านบน เราจะเห็นว่ามีการปลูกพืช 5 ต้นในแต่ละสภาวะรวมกัน ตัวอย่างเช่น ปลูกต้นไม้ 5 ต้นโดยรดน้ำทุกวันและไม่มีแสงแดด และความสูงหลังจากสองเดือนคือ 4.8 นิ้ว 4.4 นิ้ว 3.2 นิ้ว 3.9 นิ้ว และ 4.4 นิ้ว:

เราสามารถใช้ขั้นตอนต่อไปนี้เพื่อทำการวิเคราะห์ความแปรปรวนแบบสองทางกับข้อมูลนี้:

ขั้นตอนที่ 1: เลือก Data Analysis Toolpak

บนแท็บ ข้อมูล คลิก การวิเคราะห์ข้อมูล :

หากคุณไม่เห็นตัวเลือกนี้ คุณควร โหลด Data Analysis Toolpak ฟรี ก่อน

2. เลือก Anova: สองปัจจัยที่มีการจำลองแบบ

เลือกตัวเลือกที่ระบุว่า Anova: Two-Factor With Replication จากนั้นคลิก OK

ในบริบทนี้ “การจำลองแบบ” หมายถึงการสังเกตหลายครั้งในแต่ละกลุ่ม ตัวอย่างเช่น พืชหลายชนิดปลูกโดยไม่ได้รับแสงแดดและไม่มีการรดน้ำทุกวัน ถ้าเราปลูกพืชเพียงต้นเดียวในแต่ละเงื่อนไขรวมกัน เราจะใช้ “ไม่มีการจำลอง” แต่ขนาดตัวอย่างของเราจะเล็กกว่ามาก

3. กรอกค่าที่จำเป็น

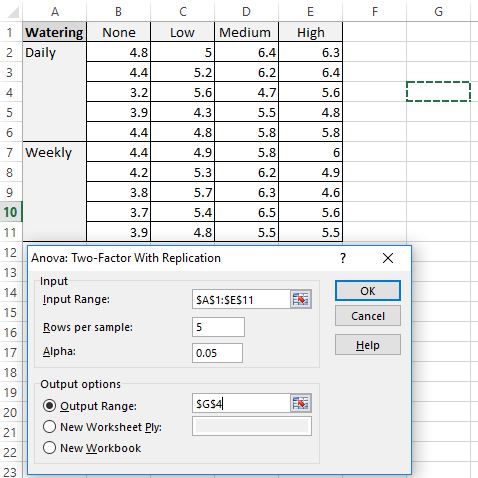
ถัดไป กรอกค่าต่อไปนี้:

• ช่วงอินพุต: เลือกช่วงของเซลล์ที่มีข้อมูลของเราอยู่ รวมถึงส่วนหัวด้วย
• แถวต่อตัวอย่าง: พิมพ์ “5” เนื่องจากแต่ละตัวอย่างมี 5 ต้น
• อัลฟ่า: เลือกระดับนัยสำคัญที่จะใช้ เราจะเลือก 0.05.
• ช่วงเอาต์พุต: เลือกเซลล์ที่คุณต้องการให้เอาต์พุต ANOVA แบบสองทางปรากฏ เราจะเลือกเซลล์ $G$4

ขั้นตอนที่ 4: ตีความผลลัพธ์

เมื่อเราคลิก OK ผลลัพธ์ของ ANOVA แบบสองทางจะปรากฏขึ้น:

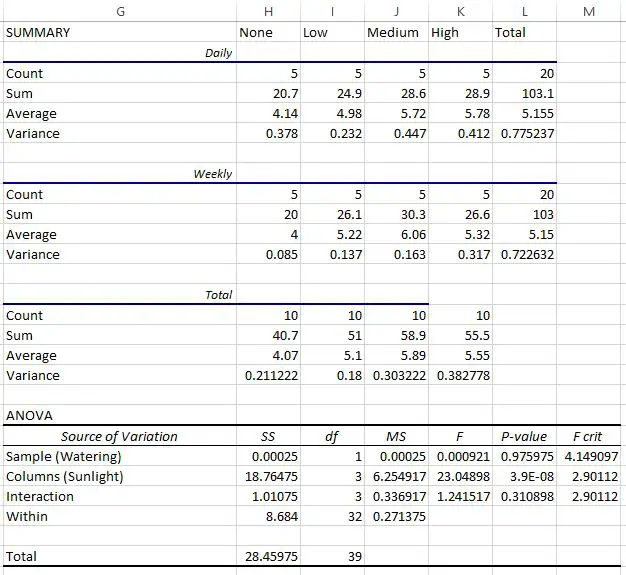
สามตารางแรกนำเสนอสถิติสรุปสำหรับแต่ละกลุ่ม ตัวอย่างเช่น:

• ความสูงเฉลี่ยของพืชที่รดน้ำทุกวันแต่ไม่มีแสงแดดคือ 4.14 นิ้ว
• ความสูงเฉลี่ยของพืชที่รดน้ำทุกสัปดาห์และได้รับแสงแดดน้อยคือ 5.22 นิ้ว
• ความสูงเฉลี่ยของพืชทั้งหมดที่รดน้ำทุกวันคือ 5.115 นิ้ว
• ความสูงเฉลี่ยของพืชทั้งหมดที่รดน้ำในแต่ละสัปดาห์คือ 5.15 นิ้ว
• ความสูงเฉลี่ยของพืชทุกชนิดภายใต้แสงแดดจัดคือ 5.55 นิ้ว

และอื่นๆ

ตารางสุดท้ายแสดงผลของการวิเคราะห์ความแปรปรวนแบบสองทาง เราสามารถสังเกตได้ดังต่อไปนี้:

• ค่า p ของปฏิสัมพันธ์ระหว่างความถี่ในการรดน้ำและแสงแดดเท่ากับ 0.310898 ซึ่งไม่มีนัยสำคัญทางสถิติที่ระดับอัลฟ่า 0.05
• ค่า p ความถี่ในการรดน้ำเท่ากับ 0.975975 ซึ่งไม่มีนัยสำคัญทางสถิติที่ระดับอัลฟ่า 0.05
• ค่า p ของการรับแสงแดดคือ 3.9E-8 (0.000000039) ซึ่งมีนัยสำคัญทางสถิติที่ระดับอัลฟา 0.05

ผลลัพธ์เหล่านี้บ่งชี้ว่าแสงแดดเป็นปัจจัยเดียวที่มีผลกระทบที่มีนัยสำคัญทางสถิติต่อความสูงของพืช และเนื่องจากไม่มีผลกระทบจากปฏิกิริยาใดๆ ผลของแสงแดดจึงสม่ำเสมอในแต่ละระดับของความถี่ในการรดน้ำ พูดง่ายๆ ก็คือ ไม่ว่าต้นไม้จะรดน้ำทุกวันหรือทุกสัปดาห์ก็ไม่มีผลกระทบต่อแสงแดดที่ส่งผลต่อต้นไม้