วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน spss

การ วิเคราะห์ความแปรปรวนแบบสองทาง ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปที่ถูกแบ่งออกเป็นสองปัจจัยหรือไม่

วัตถุประสงค์ของการวิเคราะห์ความแปรปรวนแบบสองทางคือเพื่อกำหนดผลกระทบของปัจจัยสองตัวต่อตัวแปรการตอบสนอง และเพื่อพิจารณาว่ามีการโต้ตอบระหว่างปัจจัยทั้งสองกับตัวแปรตอบสนองหรือไม่

บทช่วยสอนนี้จะอธิบายวิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน SPSS

ตัวอย่าง: การวิเคราะห์ความแปรปรวนแบบสองทางใน SPSS

นักพฤกษศาสตร์ต้องการทราบว่าการเจริญเติบโตของพืชได้รับอิทธิพลจากการสัมผัสกับแสงแดดและความถี่ในการรดน้ำหรือไม่ เธอปลูกเมล็ดพืช 30 เมล็ดและปล่อยให้มันเติบโตเป็นเวลาสองเดือนในสภาพแสงแดดและความถี่ในการรดน้ำที่แตกต่างกัน หลังจากผ่านไปสองเดือน เธอก็บันทึกความสูงของต้นแต่ละต้นเป็นหน่วยนิ้ว

ผลลัพธ์แสดงไว้ด้านล่าง:

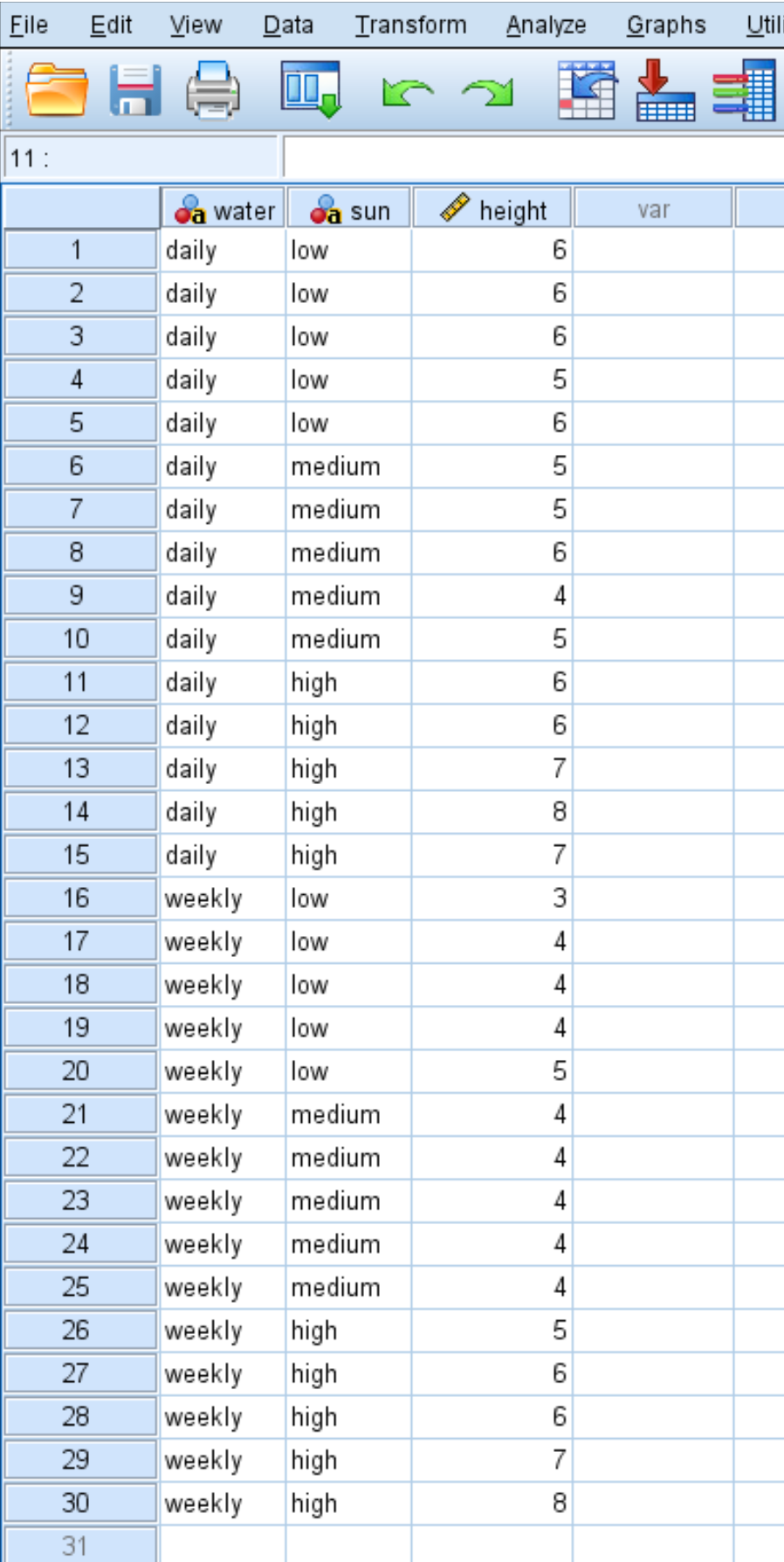
ใช้ขั้นตอนต่อไปนี้เพื่อทำการวิเคราะห์ความแปรปรวนแบบสองทางเพื่อตรวจสอบว่าความถี่ในการรดน้ำและแสงแดดมีผลกระทบอย่างมีนัยสำคัญต่อการเจริญเติบโตของพืชหรือไม่ และเพื่อตรวจสอบว่ามีผลกระทบอันตรกิริยาระหว่างความถี่ของน้ำและแสงแดดหรือไม่ รดน้ำและสัมผัสกับแสงแดด

ขั้นตอนที่ 1: ดำเนินการวิเคราะห์ความแปรปรวนแบบสองทาง

คลิกแท็บ วิเคราะห์ จากนั้นคลิก General Linear Model จากนั้นคลิก Univariate :

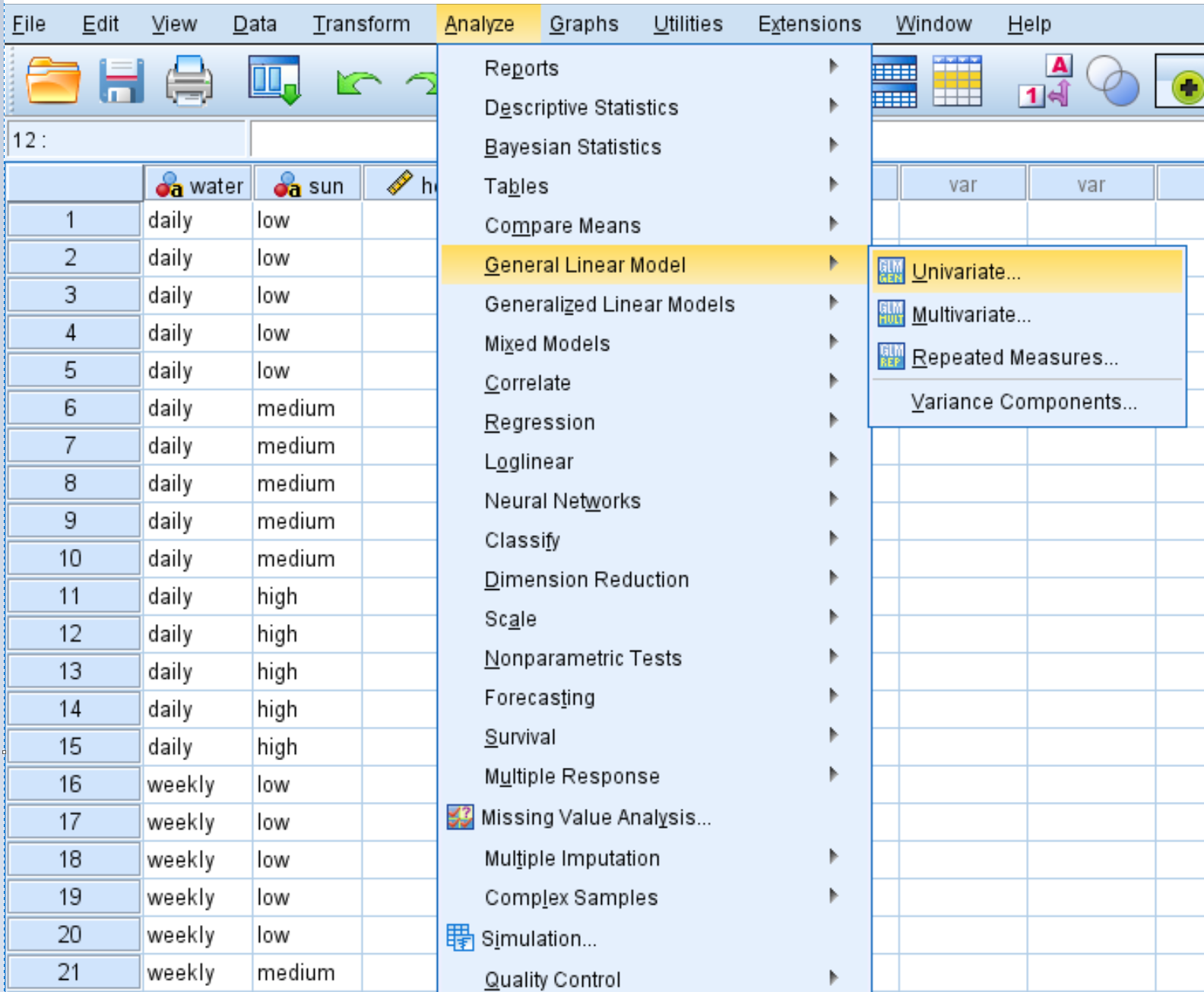
ลาก ความสูง ของตัวแปรตอบสนองลงในกล่องที่มีข้อความว่า ตัวแปรตาม ลากตัวแปรปัจจัย น้ำ และ แสงแดด สองตัวลงในช่องที่มีข้อความว่าปัจจัยคงที่:

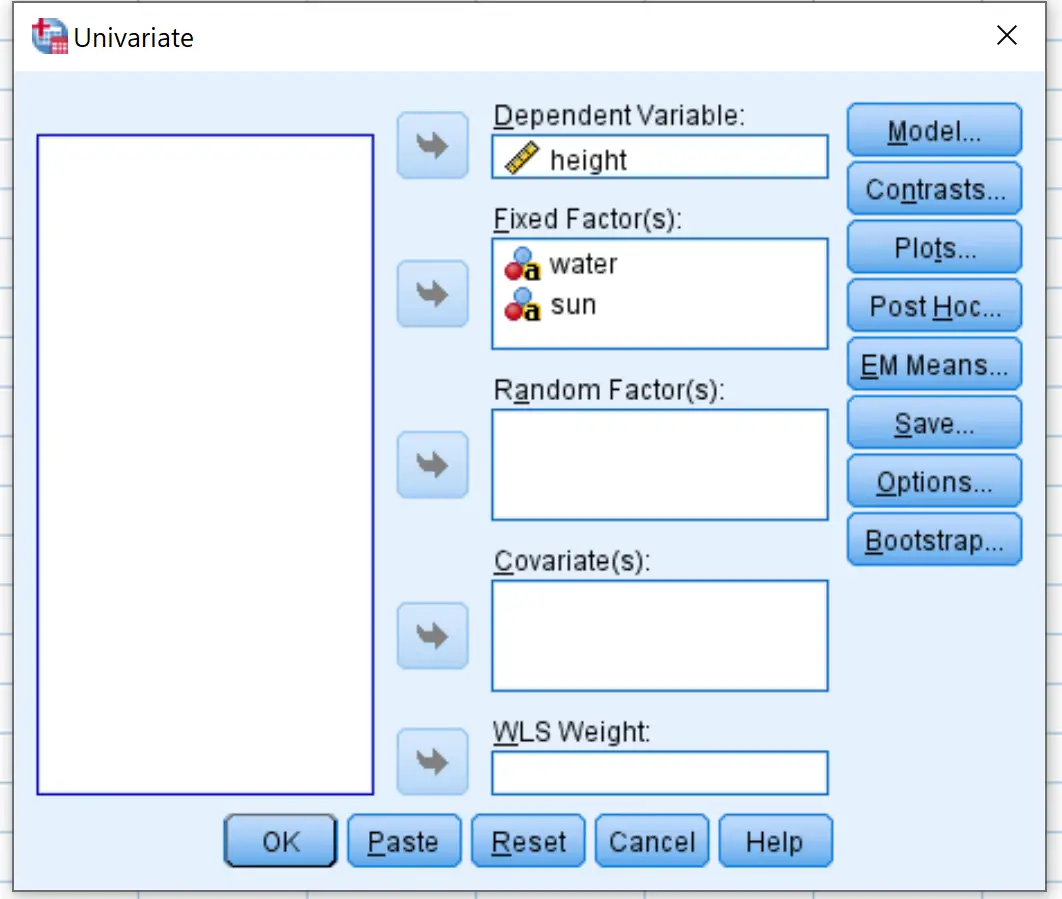
จากนั้นคลิกปุ่ม แปลง ลาก น้ำ ไปยังพื้นที่ที่มีป้ายกำกับว่าแกนนอนและ ดวงอาทิตย์ ไปยังพื้นที่ที่มีป้ายกำกับเส้นแยก จากนั้นคลิก เพิ่ม คำ ว่า น้ำ*ดวงอาทิตย์ จะปรากฏในกล่องชื่อแปลง จากนั้นคลิก ดำเนินการต่อ

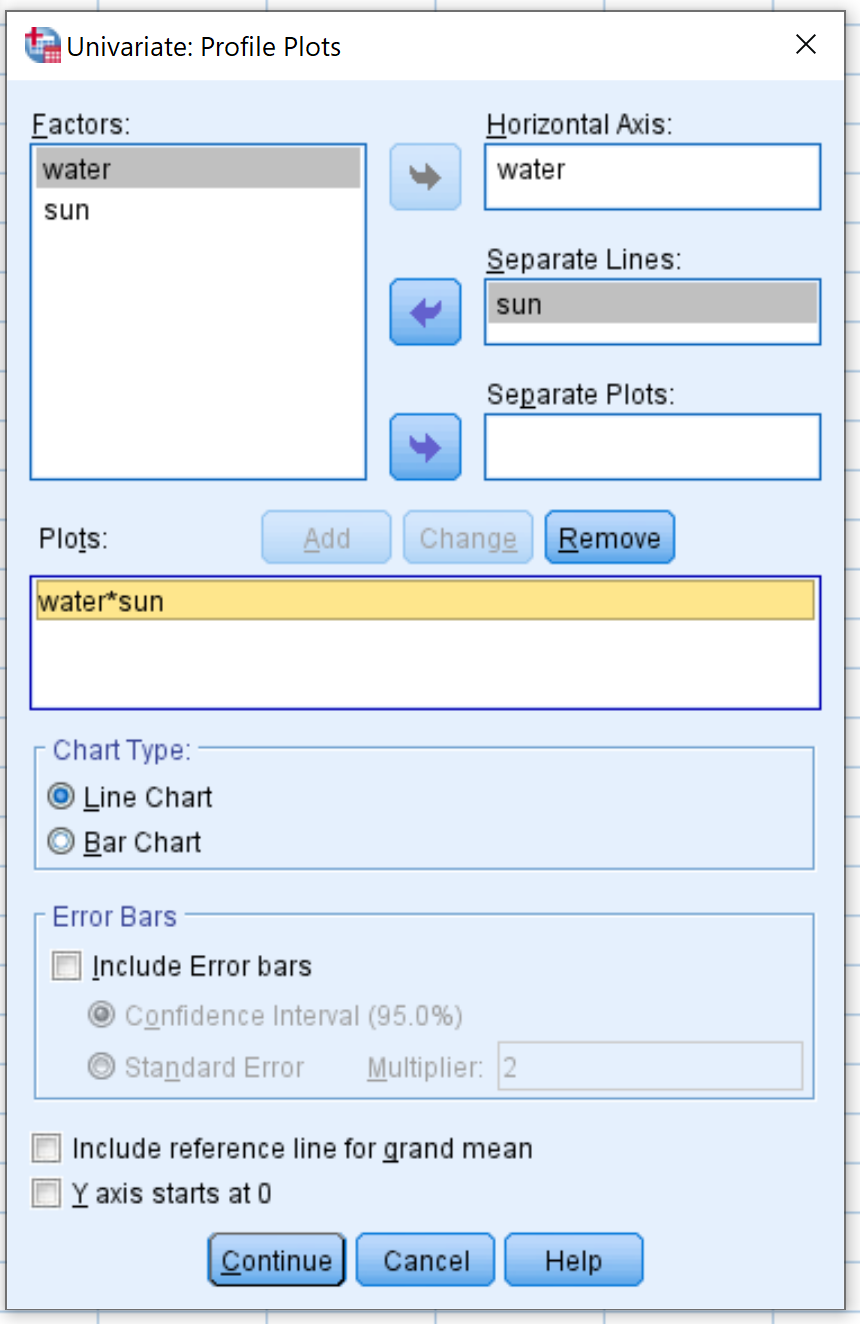
จากนั้นคลิกที่ปุ่ม Post Hoc ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ลากตัวแปร ดวงอาทิตย์ ลงในกล่องที่มีข้อความว่า Post-Hoc Tests For จากนั้นทำเครื่องหมายที่ช่องถัดจาก Tukey จากนั้นคลิก ดำเนินการต่อ

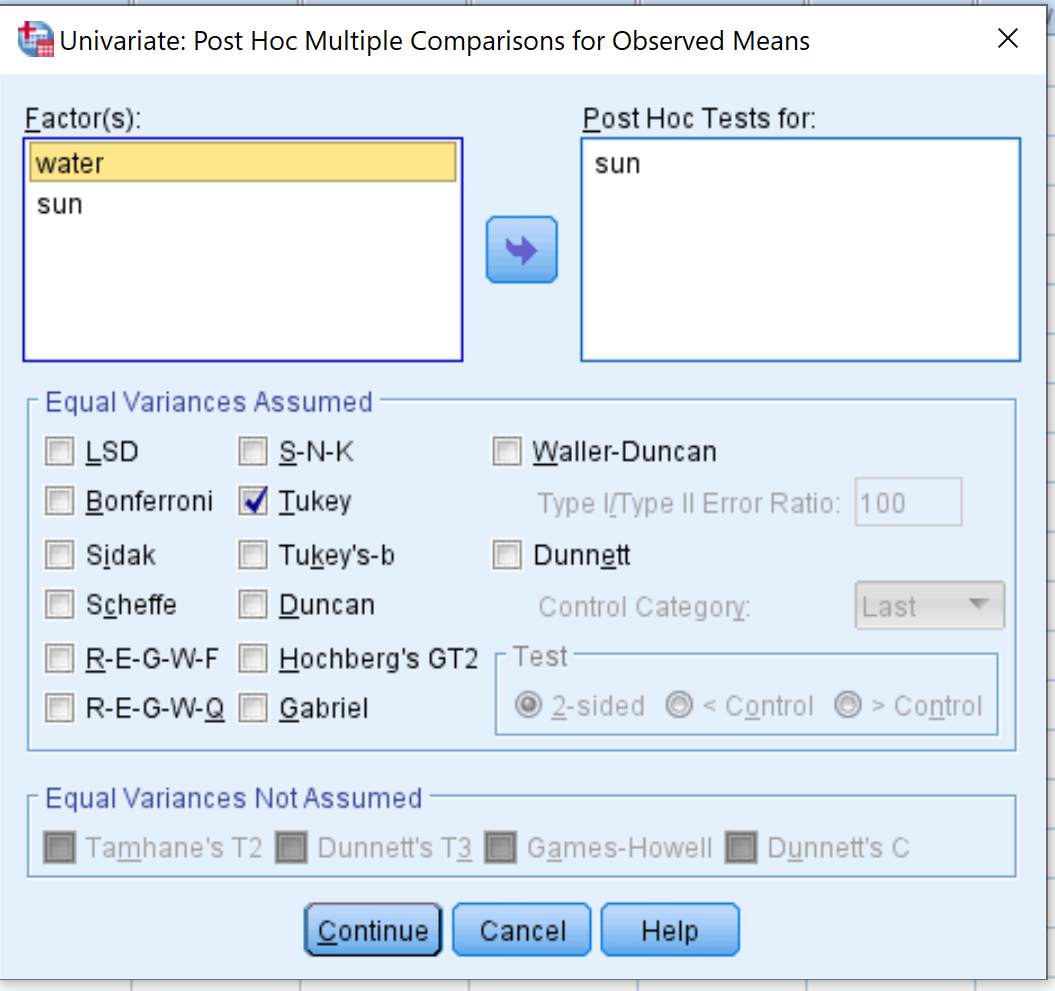
จากนั้นคลิกที่ปุ่ม EM Means ลากตัวแปรต่อไปนี้ลงในช่องที่มีข้อความแสดงค่าเฉลี่ยสำหรับ จากนั้นคลิก ดำเนินการต่อ

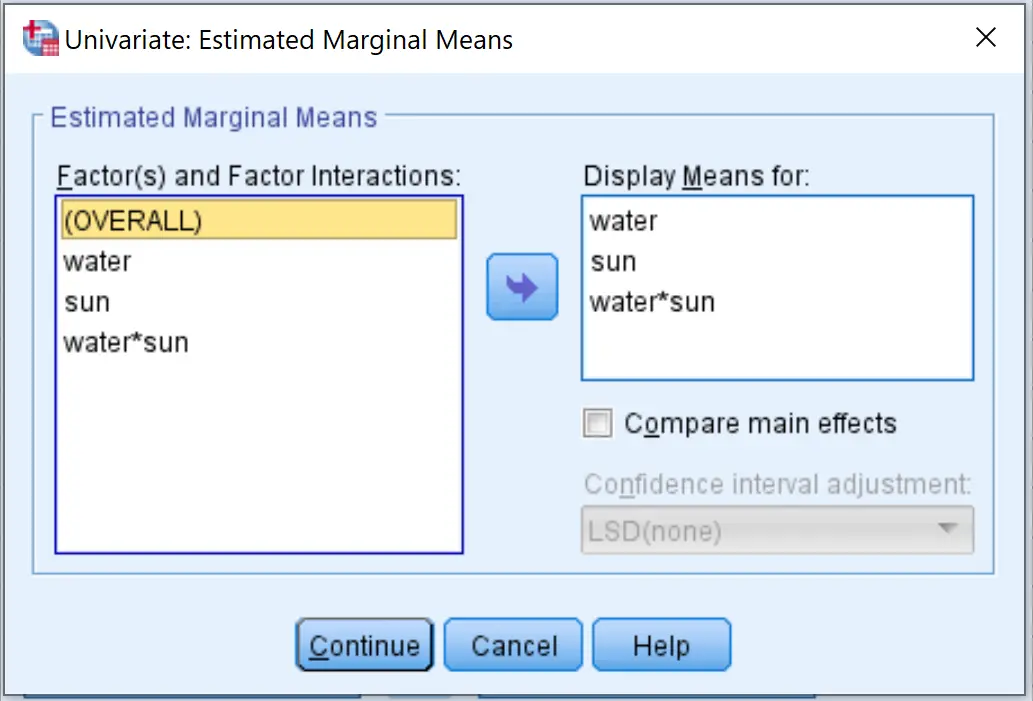
สุดท้ายคลิก ตกลง

ขั้นตอนที่ 2: ตีความผลลัพธ์

เมื่อคุณคลิก ตกลง ผลลัพธ์ ANOVA แบบสองทางจะปรากฏขึ้น ต่อไปนี้เป็นวิธีการตีความผลลัพธ์:

การทดสอบผลกระทบระหว่างวิชา

ตารางแรกแสดงค่า p สำหรับปัจจัย น้ำ และ แสงแดด รวมถึงผลกระทบจากปฏิกิริยาระหว่าง น้ำ*ดวงอาทิตย์ :

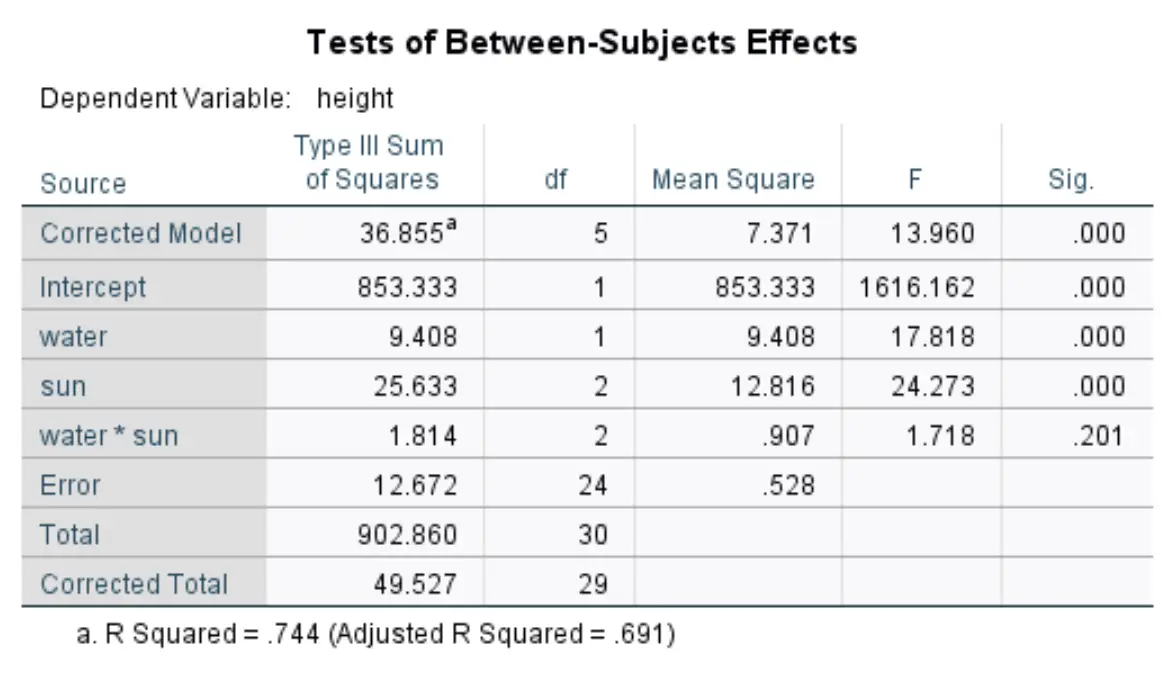
เราสามารถดูค่า p ต่อไปนี้สำหรับแต่ละปัจจัยในตาราง:

• น้ำ: ค่า p = 0.000
• ดวงอาทิตย์: ค่า p = 0.000
• น้ำ*ดวงอาทิตย์: ค่า p = 0.201

เนื่องจากค่า p ของน้ำและแสงแดดน้อยกว่า 0.05 นี่จึงบอกเราว่าปัจจัยทั้งสองมีผลกระทบที่มีนัยสำคัญทางสถิติต่อความสูงของพืช

และเนื่องจากค่า p สำหรับเอฟเฟกต์ปฏิสัมพันธ์ (0.201) มีค่าไม่น้อยกว่า 0.05 นี่จึงบอกเราว่าไม่มีผลกระทบที่มีนัยสำคัญระหว่างการสัมผัสกับแสงแดดและความถี่ของการรดน้ำ

ค่าเฉลี่ยส่วนเพิ่มโดยประมาณ

ตารางแรกจะแสดงค่าเฉลี่ยของการสังเกตสำหรับแต่ละปัจจัย:

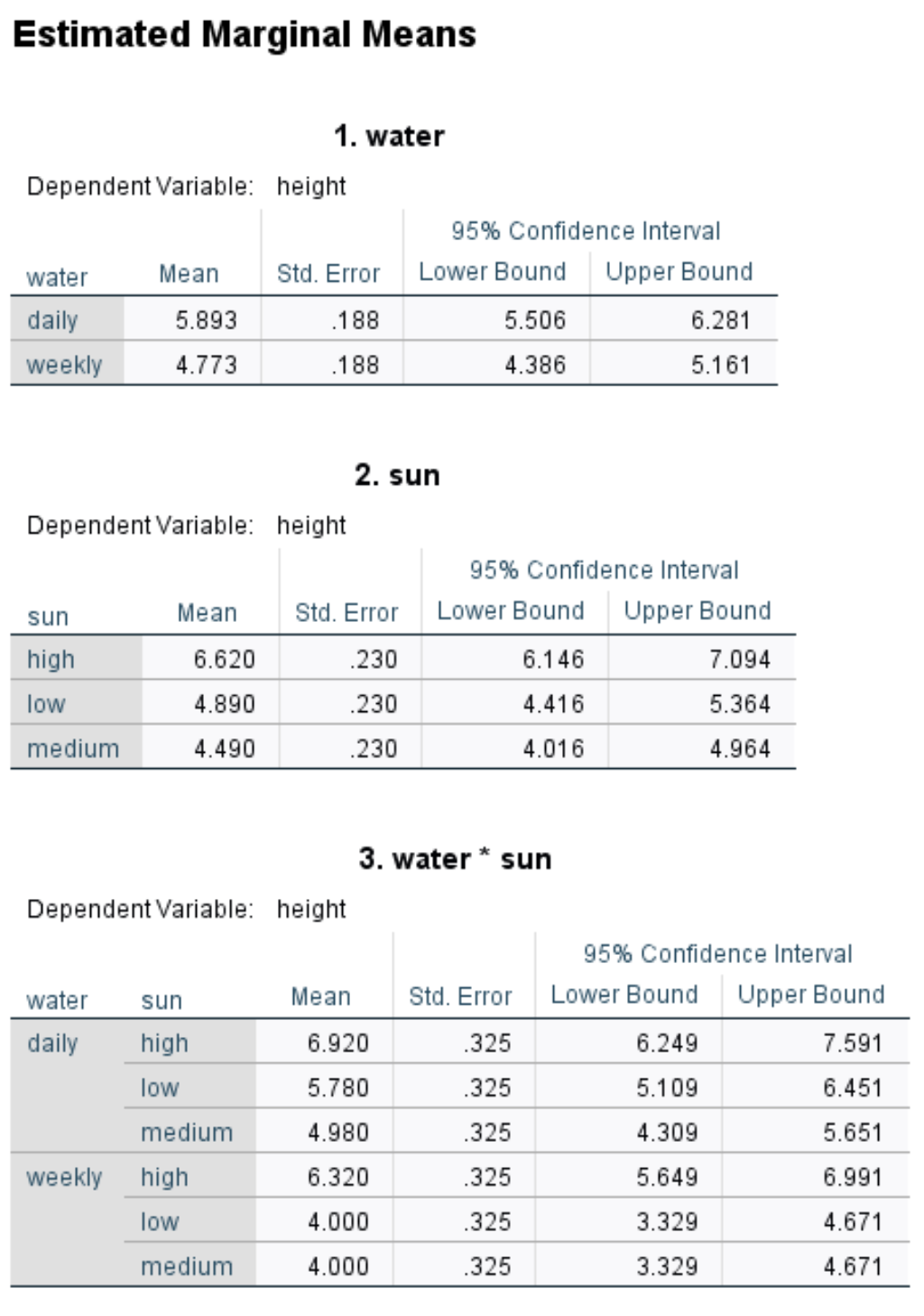
ตัวอย่างเช่น:

• ความสูงเฉลี่ยของพืชที่รดน้ำทุกวันคือ 5.893 นิ้ว
• ความสูงเฉลี่ยของพืชในแสงแดดจัดคือ 6.62 นิ้ว
• ความสูงเฉลี่ยของพืชที่รดน้ำทุกวัน และ โดนแสงแดดจัดคือ 6.32 นิ้ว

และอื่นๆ

การทดสอบหลังการทดสอบ

ตารางนี้แสดงค่า p สำหรับการเปรียบเทียบหลังกิจธุระของ Tukey ระหว่างระดับแสงแดดที่แตกต่างกันสามระดับ

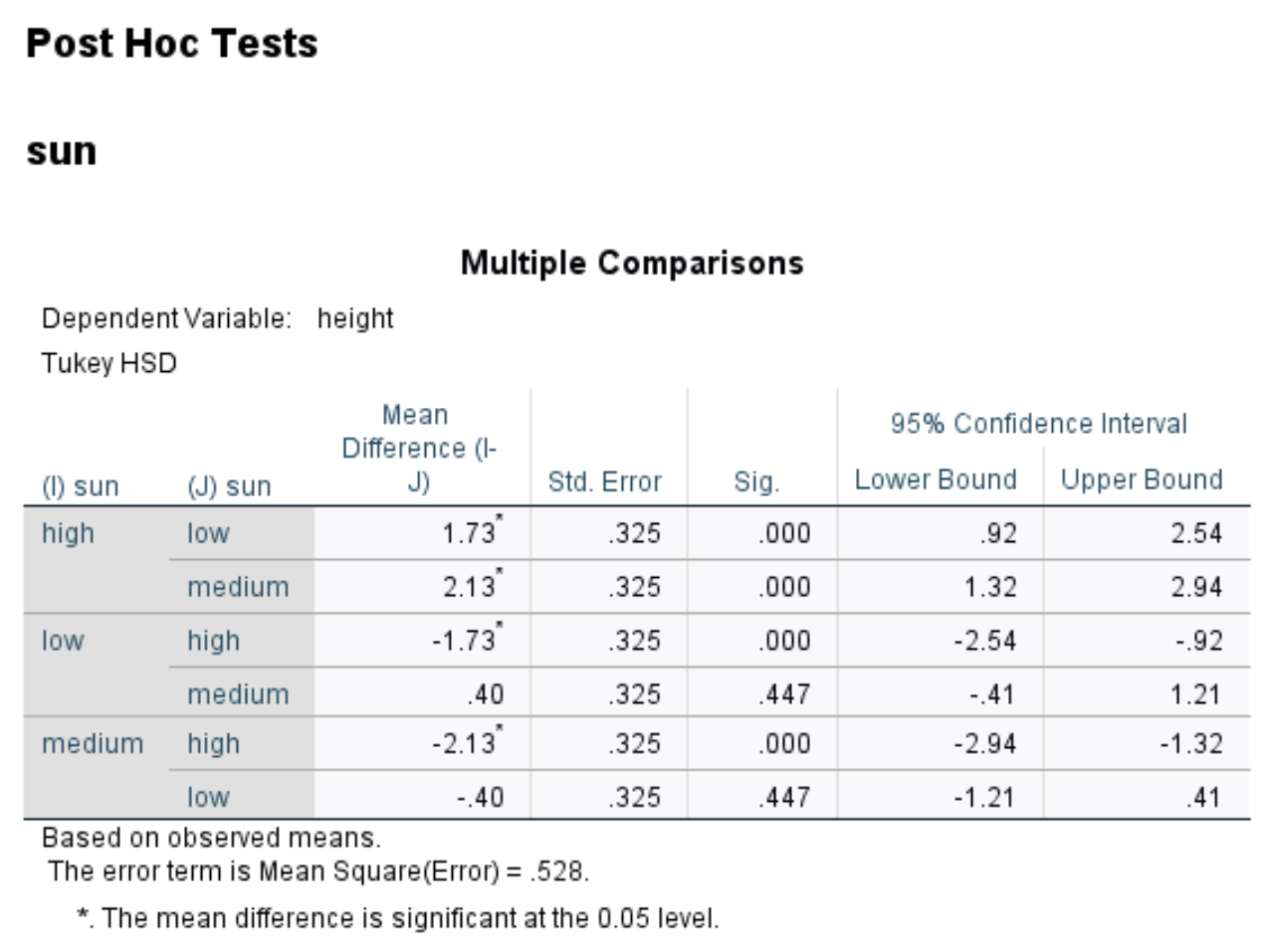
ในตารางเราจะเห็นค่า p สำหรับการเปรียบเทียบต่อไปนี้:

• เทียบกับสูง ต่ำ: | ค่า p = 0.000
• สูง vs ปานกลาง | ค่า p = 0.000
• ต่ำและปานกลาง | ค่า p = 0.447

สิ่งนี้บอกเราว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างการได้รับแสงแดดสูงและต่ำ เช่นเดียวกับการได้รับแสงแดดสูงและปานกลาง แต่ไม่มีความแตกต่างที่มีนัยสำคัญระหว่างการได้รับแสงแดดในระดับต่ำและปานกลาง

ขั้นตอนที่ 3: รายงานผลลัพธ์

สุดท้ายนี้ เราสามารถรายงานผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบสองทางได้ นี่คือตัวอย่างของวิธีการทำเช่นนี้:

ทำการวิเคราะห์ความแปรปรวนแบบสองทางเพื่อพิจารณาว่าความถี่ในการรดน้ำ (รายวันหรือรายสัปดาห์) และการสัมผัสกับแสงแดด (ต่ำ ปานกลาง สูง) มีผลกระทบอย่างมีนัยสำคัญต่อการเจริญเติบโตของพืชหรือไม่ มีการใช้พืชทั้งหมด 30 ต้นในการศึกษา

การวิเคราะห์ความแปรปรวนแบบสองทางเผยให้เห็นว่าความถี่ในการรดน้ำ (p < 0.000) และการสัมผัสแสงแดด (p < 0.000) ทั้งคู่มีผลกระทบที่มีนัยสำคัญทางสถิติต่อการเจริญเติบโตของพืช

พืชที่รดน้ำทุกวันมีการเจริญเติบโตสูงกว่าพืชที่รดน้ำทุกสัปดาห์อย่างมีนัยสำคัญ

นอกจากนี้ การทดสอบของ Tukey สำหรับการเปรียบเทียบหลายรายการพบว่าพืชที่ได้รับแสงแดดสูงมีการเจริญเติบโตสูงกว่าพืชที่ได้รับแสงแดดปานกลางหรือต่ำอย่างมีนัยสำคัญ อย่างไรก็ตาม ไม่มีความแตกต่างที่มีนัยสำคัญระหว่างพืชที่ได้รับแสงแดดปานกลางและต่ำ

นอกจากนี้ยังไม่มีผลกระทบที่มีนัยสำคัญทางสถิติระหว่างความถี่ในการรดน้ำและแสงแดด