วิธีการดำเนินการวัดความแปรปรวนซ้ำ ๆ ด้วยตนเอง
การวัดความแปรปรวนแบบวัดซ้ำ จะถูกนำมาใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มตั้งแต่สามกลุ่มขึ้นไปซึ่งมีหัวข้อเดียวกันปรากฏในแต่ละกลุ่มหรือไม่
บทช่วยสอนนี้จะอธิบายวิธีการดำเนินการวัดความแปรปรวนแบบทางเดียวด้วยตนเองด้วยตนเอง
ตัวอย่าง: การวัดความแปรปรวนแบบทางเดียวซ้ำๆ ด้วยมือ
นักวิจัยต้องการทราบว่ายาสามชนิดทำให้เกิดปฏิกิริยาต่างกันหรือไม่ เพื่อทดสอบสิ่งนี้ พวกเขาวัดเวลาปฏิกิริยา (เป็นวินาที) ของผู้ป่วยห้ารายต่อยาแต่ละชนิด ผลลัพธ์แสดงไว้ด้านล่าง:
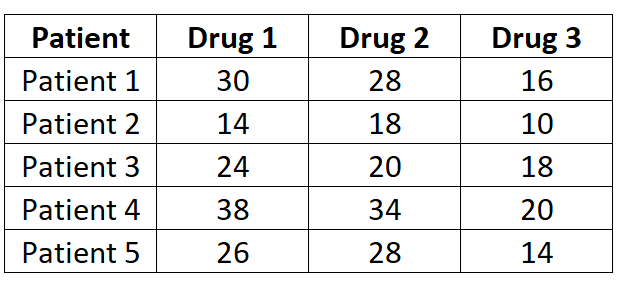
เนื่องจากผู้ป่วยแต่ละรายได้รับการวัดด้วยยาแต่ละชนิดจากทั้งหมด 3 ชนิด เราจะใช้การวัดความแปรปรวนแบบวัดซ้ำแบบทางเดียวเพื่อตรวจสอบว่าเวลาเฉลี่ยของปฏิกิริยาแตกต่างกันระหว่างยาแต่ละชนิดหรือไม่
ทำตามขั้นตอนต่อไปนี้เพื่อดำเนินการวัด ANOVA ซ้ำด้วยตนเอง:
ขั้นตอนที่ 1: คำนวณ SST
ขั้นแรก เราจะคำนวณผลรวมของกำลังสอง (SST) ซึ่งหาได้จากสูตรต่อไปนี้:
SST = รวม s 2 ( รวม n -1)
ทอง:
- รวม s 2 : ความแปรปรวนของชุดข้อมูล
- n ทั้งหมด : จำนวนการสังเกตทั้งหมดในชุดข้อมูล
ในตัวอย่างนี้ เราคำนวณ SST ดังนี้: (64.2667)(15-1) = 899.7
ขั้นตอนที่ 2: คำนวณ SSB
ต่อไป เราจะคำนวณผลรวมของกำลังสอง (SSB) ซึ่งหาได้จากสูตรต่อไปนี้:
SSB = Σn j ( x j – x รวม ) 2
ทอง:
- Σ : สัญลักษณ์กรีกหมายถึง “ผลรวม”
- n j : จำนวนการสังเกตทั้งหมดในกลุ่ม ที่ j
- x j : ค่าเฉลี่ยของกลุ่ม j
- x รวม : ค่าเฉลี่ยของข้อมูลทั้งหมด
ในตัวอย่างนี้ เราคำนวณ SSB ดังต่อไปนี้: (5)(26.4-22.533) 2 +(5)(25.6-22.533) 2 + (5)(15.6-22.533) 2 = 362.1
ขั้นตอนที่ 3: คำนวณ SSS
ต่อไป เราจะคำนวณผลรวมของกำลังสอง (SSS) ซึ่งหาได้จากสูตรต่อไปนี้:
SSS =(Σr 2 k /c) – (N 2 /rc)
ทอง:
- Σ : สัญลักษณ์กรีกหมายถึง “ผลรวม”
- r 2 k : ผลรวมกำลังสองของผู้ป่วย k
- N: ผลรวมทั้งหมดของข้อมูลทั้งหมด
- r: จำนวนผู้ป่วยทั้งหมด
- c: จำนวนกลุ่มทั้งหมด
ในตัวอย่างนี้ เราคำนวณ SSS ดังต่อไปนี้: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441.1
ขั้นตอนที่ 4: คำนวณ SES
ต่อไป เราจะคำนวณผลรวมของความคลาดเคลื่อนกำลังสอง (SSE) ซึ่งหาได้โดยใช้สูตรต่อไปนี้:
SSE = SST – SSB – SSS
ในตัวอย่างนี้ เราคำนวณ SES ดังต่อไปนี้: 899.7 – 362.1 – 441.1 = 96.5
ขั้นตอนที่ 5: ทำตาราง ANOVA การวัดซ้ำให้สมบูรณ์
ตอนนี้เรามี SSB, SSS และ SSE แล้ว เราสามารถเติมข้อมูลตาราง ANOVA การวัดซ้ำได้:
| แหล่งที่มา | ผลรวมของกำลังสอง (SS) | df | ค่าเฉลี่ยกำลังสอง (MS) | เอฟ |
|---|---|---|---|---|
| ระหว่าง | 362.1 | 2 | 181.1 | 15.006 |
| เรื่อง | 441.1 | 4 | 110.3 | |
| ข้อผิดพลาด | 96.5 | 8 | 12.1 |
นี่คือวิธีที่เราคำนวณตัวเลขต่างๆ ในตาราง:
- df ระหว่าง: #groups – 1 = 3 – 1 = 2
- หัวข้อ df: #ผู้เข้าร่วม – 1 = 5 – 1 = 4
- ข้อผิดพลาด df: df ระหว่าง * df subject = 2*4 = 8
- MS เข้าสู่: SSB / df เข้าสู่ = 362.1 / 2 = 181.1
- หัวเรื่อง MS: หัวเรื่อง SSS / df = 441.1 / 4 = 110.3
- ข้อผิดพลาด MS: ข้อผิดพลาด SSE / df = 96.5 / 8 = 12.1
- F: MS เข้าสู่ / ข้อผิดพลาด MS = 181.1 / 12.1 = 15.006
ขั้นตอนที่ 6: ตีความผลลัพธ์
สถิติการทดสอบ F สำหรับการวัดความแปรปรวนแบบทางเดียวนี้คือ 15.006 ในการพิจารณาว่านี่เป็นผลลัพธ์ที่มีนัยสำคัญทางสถิติหรือไม่ เราจำเป็นต้องเปรียบเทียบกับค่า F วิกฤตที่พบในตาราง การแจกแจง F ด้วยค่าต่อไปนี้:
- α (ระดับนัยสำคัญ) = 0.05
- DF1 (องศาอิสระของตัวเศษ) = df ระหว่าง = 2
- DF2 (องศาอิสระของตัวส่วน) = ข้อผิดพลาด df = 8
เราพบว่าค่าวิกฤตของ F คือ 4.459
เนื่องจากสถิติการทดสอบ F ในตาราง ANOVA มากกว่าค่าวิกฤต F ในตารางการแจกแจง F เราจึงปฏิเสธสมมติฐานว่าง ซึ่งหมายความว่า เรามีหลักฐานเพียงพอที่จะบอกว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างเวลาตอบสนองโดยเฉลี่ยของยา