วิธีดำเนินการ anova แบบสองทางใน sas

การวิเคราะห์ความแปรปรวนแบบสองทาง ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระตั้งแต่ 3 กลุ่มขึ้นไปที่กำหนดให้กับตัวแปรสองตัว (บางครั้งเรียกว่า “ปัจจัย”) หรือไม่

บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีดำเนินการ ANOVA แบบสองทางใน SAS

ขั้นตอนที่ 1: สร้างข้อมูล

สมมติว่านักพฤกษศาสตร์ต้องการทราบว่าการเจริญเติบโตของพืชได้รับอิทธิพลจากการได้รับแสงแดดและความถี่ในการรดน้ำหรือไม่

เธอปลูกเมล็ดพืช 30 เมล็ดและปล่อยให้มันเติบโตเป็นเวลาหนึ่งเดือนในสภาพแสงแดดและความถี่ในการรดน้ำที่แตกต่างกัน หลังจากผ่านไปหนึ่งเดือน เธอก็บันทึกความสูงของต้นแต่ละต้น ผลลัพธ์แสดงไว้ด้านล่าง:

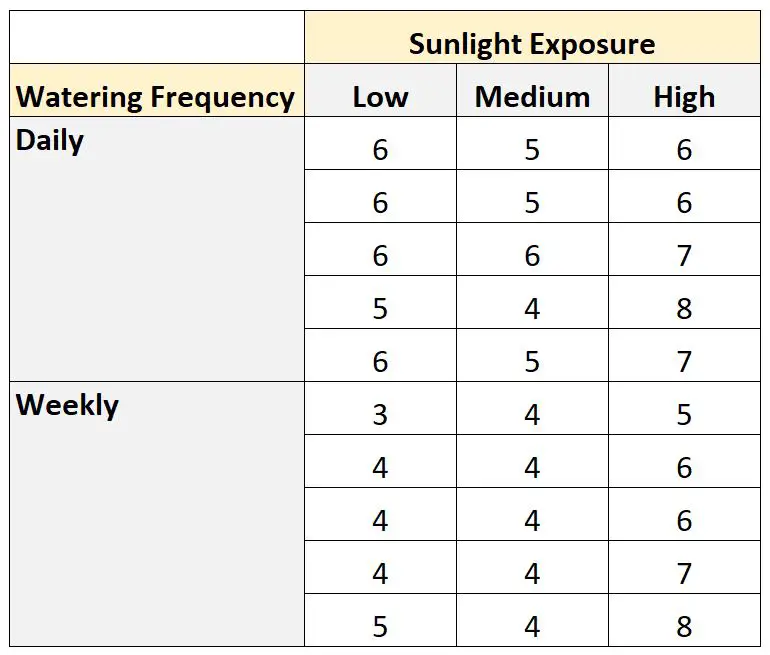
เราสามารถใช้โค้ดต่อไปนี้เพื่อสร้างชุดข้อมูลนี้ใน SAS:

 /*create dataset*/
data my_data;
    input water $sunlight $height;
    datalines ;
daily low 6
daily low 6
daily low 6
daily low 5
daily low 6
daily med 5
daily med 5
daily med 6
daily med 4
daily med 5
daily high 6
daily high 6
daily high 7
daily high 8
daily high 7
weekly low 3
weekly low 4
weekly low 4
weekly low 4
weekly low 5
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly high 5
weekly high 6
weekly high 6
weekly high 7
weekly high 8
;
run ;

ขั้นตอนที่ 2: ดำเนินการวิเคราะห์ความแปรปรวนแบบสองทาง

ต่อไป เราจะใช้ proc ANOVA เพื่อทำการวิเคราะห์ความแปรปรวนแบบสองทาง:

 /*perform two-way ANOVA*/
proc ANOVA data =my_data;
class water sunlight;
model height = water sunlight water*sunlight;
means water sunlight / tukey cldiff ;
run ;

ขั้นตอนที่ 3: ตีความผลลัพธ์

ตารางแรกที่เราต้องการวิเคราะห์ในผลลัพธ์คือตาราง ANOVA:

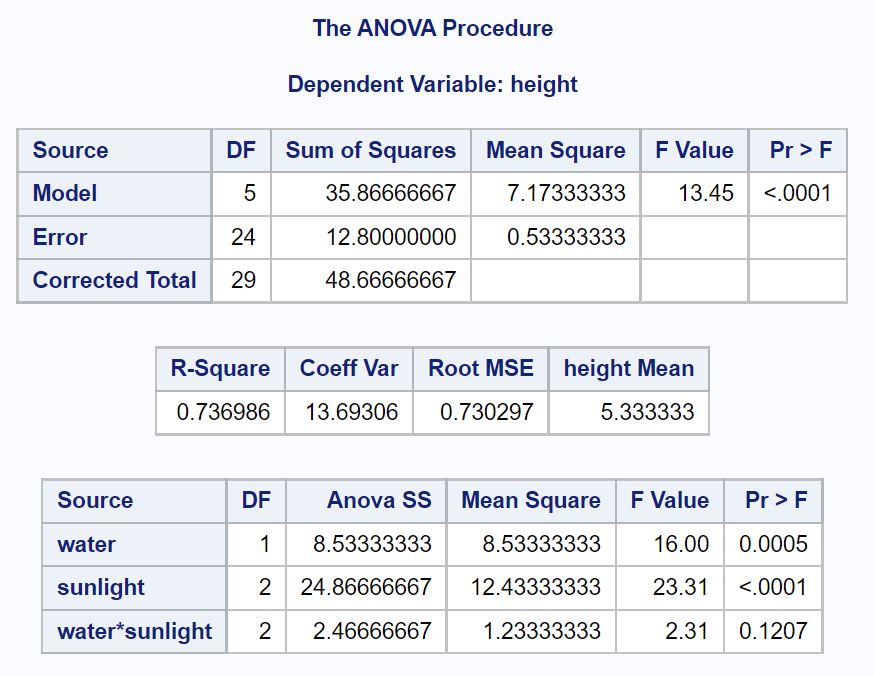
จากตารางนี้เราจะเห็น:

• ค่า p สำหรับน้ำ: 0.0005
• ค่า p สำหรับแสงแดด: <.0001
• ค่า p ของปฏิกิริยาระหว่างน้ำกับแสงแดด: 1207

สิ่งนี้บอกเราว่าน้ำและแสงแดดเป็นตัวทำนายความสูงของพืชที่มีนัยสำคัญทางสถิติ และไม่มีผลกระทบอันมีนัยสำคัญทางสถิติระหว่างน้ำและแสงแดด

ต่อไป เราสามารถตรวจสอบผลลัพธ์ของการทดสอบหลังการทดสอบของ Tukey เพื่อพิจารณาว่าระดับน้ำและแสงแดดใดที่แตกต่างกันอย่างมีนัยสำคัญทางสถิติ

อันดับแรก เราจะดูการเปรียบเทียบน้ำหลังการดำเนินการของ Tukey:

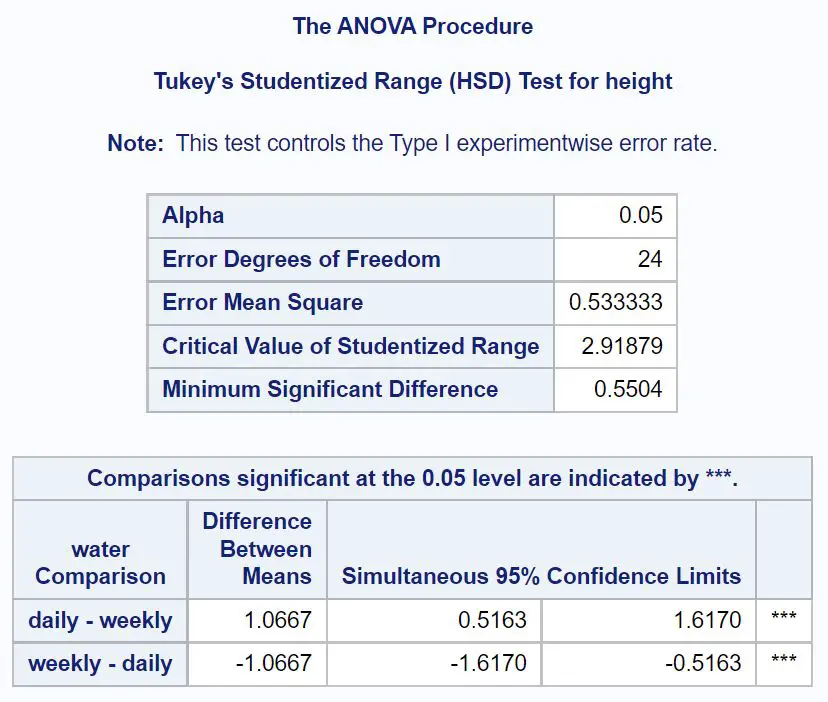
จากผลการวิจัย เราจะเห็นว่าความสูงเฉลี่ยระหว่างต้นไม้ที่รดน้ำรายวันและรายสัปดาห์อยู่ที่ 1.0667 นิ้ว

ช่วงความเชื่อมั่น 95% สำหรับความแตกต่างของขนาดเฉลี่ยคือ [.5163, 1.6170] ซึ่งหมายความว่าเรามั่นใจ 95% ว่าความแตกต่างที่แท้จริงในความสูงเฉลี่ยระหว่างต้นไม้ที่รดน้ำทุกวันและต้นไม้ที่รดน้ำทุกสัปดาห์คือระหว่าง 0.5163 นิ้วถึง 1.6170 นิ้ว

อันดับแรก เราจะดูการเปรียบเทียบหลังเหตุการณ์ของ Tukey เกี่ยวกับแสงแดด:

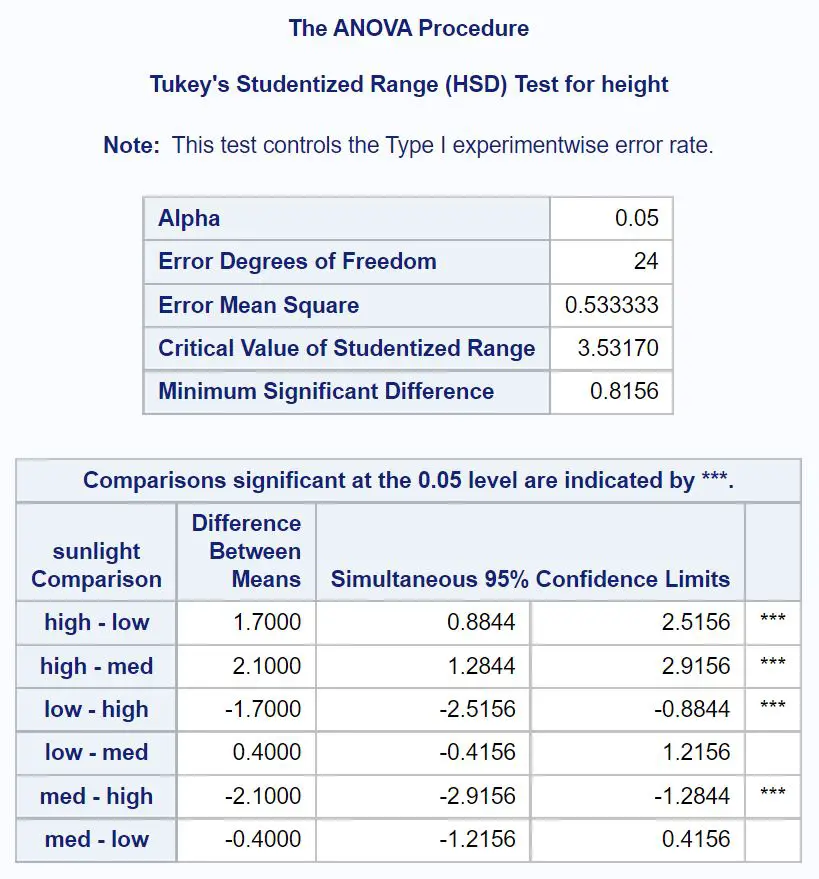
หากต้องการทราบว่าค่าเฉลี่ยของกลุ่มใดแตกต่างกัน เราต้องดูว่าการเปรียบเทียบแบบคู่ใดมีดาว ( *** ) อยู่ข้างๆ

จากตาราง เราจะเห็นว่าค่าเฉลี่ยของกลุ่มต่อไปนี้มีความแตกต่างกันอย่างมีนัยสำคัญทางสถิติ:

• แสงแดดจัดหรือแสงแดดน้อย (95% CI = [.8844, 2.5156])
• แสงแดดสูงหรือแสงแดดปานกลาง (95% CI = [1.2844, 2.9156])

ขั้นตอนที่ 4: รายงานผลลัพธ์

สุดท้ายนี้ เราสามารถ รายงานผลลัพธ์ ของการวิเคราะห์ความแปรปรวนแบบสองทางได้:

ทำการวิเคราะห์ความแปรปรวนแบบสองทางเพื่อวิเคราะห์ผลของความถี่ในการรดน้ำและแสงแดดต่อการเจริญเติบโตของพืช

การวิเคราะห์ความแปรปรวนแบบสองทางเปิดเผยว่าไม่มีปฏิสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่างผลกระทบของความถี่ในการรดน้ำและแสงแดด (p = 0.1207)

การวิเคราะห์ผลกระทบของมืออย่างง่ายแสดงให้เห็นว่าความถี่ในการรดน้ำมีผลอย่างมีนัยสำคัญต่อการเจริญเติบโตของพืช (p = 0.0005)

การวิเคราะห์ผลกระทบของมืออย่างง่ายแสดงให้เห็นว่าแสงแดดยังส่งผลต่อการเจริญเติบโตของพืชอย่างมีนัยสำคัญทางสถิติ (p < 0.0001)

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับการวิเคราะห์ความแปรปรวนแบบสองทาง:

ข้อมูลเบื้องต้นเกี่ยวกับการวิเคราะห์ความแปรปรวนแบบสองทาง
การวิเคราะห์ความแปรปรวนทางเดียวหรือสองทาง: ควรใช้เมื่อใด
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางด้วยตนเอง