วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางด้วยตนเอง
การวิเคราะห์ความแปรปรวนแบบสองทาง ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปที่ถูกแบ่งออกเป็นสองปัจจัยหรือไม่
บทช่วยสอนนี้จะอธิบายวิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางด้วยตนเอง
ตัวอย่าง: การวิเคราะห์ความแปรปรวนสองทางด้วยตนเอง
สมมติว่านักพฤกษศาสตร์ต้องการทราบว่าการเจริญเติบโตของพืชได้รับอิทธิพลจากการได้รับแสงแดดและความถี่ในการรดน้ำหรือไม่ เธอปลูกเมล็ดพืช 40 เมล็ดและปล่อยให้มันเติบโตเป็นเวลาหนึ่งเดือนในสภาพแสงแดดและความถี่ในการรดน้ำที่แตกต่างกัน
หลังจากผ่านไปหนึ่งเดือน เธอก็บันทึกความสูงของต้นแต่ละต้น ผลลัพธ์แสดงไว้ด้านล่าง:

ในตารางด้านบน เราจะเห็นว่ามีการปลูกพืช 5 ต้นในแต่ละสภาวะรวมกัน
ตัวอย่างเช่น ปลูกต้นไม้ 5 ต้นโดยรดน้ำทุกวันและไม่มีแสงแดด และความสูงหลังจากสองเดือนคือ 4.8 นิ้ว 4.4 นิ้ว 3.2 นิ้ว 3.9 นิ้ว และ 4.4 นิ้ว:

เราสามารถใช้ขั้นตอนต่อไปนี้เพื่อทำการวิเคราะห์ความแปรปรวนแบบสองทาง:
ขั้นตอนที่ 1: คำนวณผลรวมของกำลังสองสำหรับปัจจัยแรก (ความถี่ในการรดน้ำ)
ขั้นแรก เราจะคำนวณความสูงเฉลี่ยโดยรวมของต้นไม้ทั้ง 40 ต้น:
ค่าเฉลี่ยโดยรวม = (4.8 + 5 + 6.4 + 6.3 + … + 3.9 + 4.8 + 5.5 + 5.5) / 40 = 5.1525
ต่อไป เราจะคำนวณความสูงเฉลี่ยของพืชทั้งหมดที่รดน้ำทุกวัน:
ค่าเฉลี่ยรายวัน = (4.8 + 5 + 6.4 + 6.3 + … + 4.4 + 4.8 + 5.8 + 5.8) /20 = 5.155
ต่อไป เราจะคำนวณความสูงเฉลี่ยของพืชทั้งหมดที่รดน้ำในแต่ละสัปดาห์:
ค่าเฉลี่ยรายสัปดาห์ = (4.4 + 4.9 + 5.8 + 6 + … + 3.9 + 4.8 + 5.5 + 5.5) /20 = 5.15
ต่อไป เราจะคำนวณผลรวมของกำลังสองสำหรับปัจจัย “ความถี่ในการรดน้ำ” โดยใช้สูตรต่อไปนี้:
Σn(X เจ – X ..) 2
ทอง:
- n : ขนาดของกลุ่มตัวอย่าง j
- Σ : สัญลักษณ์กรีกหมายถึง “ผลรวม”
- X j : ค่าเฉลี่ยของกลุ่ม j
- X .. : ค่าเฉลี่ยที่ยอดเยี่ยม
ในตัวอย่างของเรา เราคำนวณผลรวมของกำลังสองสำหรับปัจจัย “ความถี่ในการรดน้ำ” ดังนี้: 20(5.155-5.1525) 2 + 20(5.15-5.1525) 2 = 0.00025
ขั้นตอนที่ 2: คำนวณผลรวมของกำลังสองสำหรับปัจจัยที่สอง (แสงแดด)
ขั้นแรก เราจะคำนวณความสูงเฉลี่ยโดยรวมของต้นไม้ทั้ง 40 ต้น:
ค่าเฉลี่ยโดยรวม = (4.8 + 5 + 6.4 + 6.3 + … + 3.9 + 4.8 + 5.5 + 5.5) / 40 = 5.1525
ต่อไป เราจะคำนวณความสูงเฉลี่ยของพืชทั้งหมดที่ไม่ได้รับแสงแดด:
ค่าเฉลี่ยที่ไม่มีดวงอาทิตย์ = (4.8 + 4.4 + 3.2 + 3.9 + 4.4 + 4.4 + 4.2 + 3.8 + 3.7 + 3.9) / 10 = 4.07
เราจะทำการคำนวณนี้ซ้ำเพื่อค้นหาความสูงเฉลี่ยของพืชที่ได้รับแสงแดดต่างๆ:
- ค่าเฉลี่ยแสงแดดต่ำ = 5.1
- แสงแดดเฉลี่ยเฉลี่ย = 5.89
- แสงแดดสูงเฉลี่ย = 5.55
ต่อไป เราจะคำนวณผลรวมของกำลังสองสำหรับปัจจัย “แสงแดด” โดยใช้สูตรต่อไปนี้:
Σn(X เจ – X ..) 2
ทอง:
- n : ขนาดของกลุ่มตัวอย่าง j
- Σ : สัญลักษณ์กรีกหมายถึง “ผลรวม”
- X j : ค่าเฉลี่ยของกลุ่ม j
- X .. : ค่าเฉลี่ยที่ยอดเยี่ยม
ในตัวอย่างของเรา เราคำนวณผลรวมของกำลังสองสำหรับปัจจัย “แสงแดด” ดังนี้: 10(4.07-5.1525) 2 + 10(5.1-5.1525) 2 + 10(5.89 -5.1525) 2 + 10(5.55-5.1525) 2 = 18.76475
ขั้นตอนที่ 3: คำนวณผลรวมของกำลังสองภายใน (ข้อผิดพลาด)
ต่อไป เราจะคำนวณผลรวมของกำลังสองโดยนำผลรวมของกำลังสองของความแตกต่างระหว่างแต่ละปัจจัยรวมกันและความสูงของต้นไม้แต่ละต้น
ตัวอย่างเช่น ความสูงเฉลี่ยของพืชทั้งหมดที่รดน้ำทุกวันโดยไม่โดนแสงแดดคือ 4.14 จากนั้นเราสามารถคำนวณผลรวมของกำลังสองของความแตกต่างสำหรับพืชแต่ละชนิดได้ดังนี้:
- SS สำหรับการรดน้ำทุกวันและไม่มีแสงแดด: (4.8-4.14) 2 + (4.4-4.14) 2 + (3.2-4.14) 2 + (3.9-4.14) 2 + (4.4-4.14) 2 = 1.512
เราสามารถทำซ้ำขั้นตอนนี้สำหรับปัจจัยแต่ละอย่างรวมกัน:
- SS สำหรับการรดน้ำทุกวันและแสงแดดน้อย: 0.928
- SS สำหรับการรดน้ำทุกวันและแสงแดดเฉลี่ย: 1,788
- SS สำหรับการรดน้ำทุกวันและแสงแดดจ้า: 1.648
- SS สำหรับการรดน้ำรายสัปดาห์โดยไม่มีแสงแดด: 0.34
- SS สำหรับการรดน้ำรายสัปดาห์และแสงแดดน้อย: 0.548
- SS สำหรับการรดน้ำรายสัปดาห์และแสงแดดเฉลี่ย: 0.652
- SS สำหรับการรดน้ำรายสัปดาห์และแสงแดดจ้า: 1,268
จากนั้นเราสามารถนำผลรวมของค่าเหล่านี้ทั้งหมดเพื่อหาผลรวมของกำลังสองภายใน (ข้อผิดพลาด):
ผลรวมของกำลังสองภายใน = 1.512 + 0.928 + 1.788 + 1.648 + 0.34 + 0.548 + 0.652 + 1.268 = 8.684
ขั้นตอนที่ 4: คำนวณผลรวมของกำลังสอง
จากนั้นเราสามารถคำนวณผลรวมของกำลังสองโดยนำผลรวมของความแตกต่างระหว่างความสูงของต้นแต่ละต้นกับค่าเฉลี่ยทั้งหมด:
ผลรวมของกำลังสอง = (4.8 – 5.1525) 2 + (5 – 5.1525) 2 + … + (5.5 – 5.1525) 2 = 28.45975
ขั้นตอนที่ 5: คำนวณผลรวมของการโต้ตอบกำลังสอง
ต่อไป เราจะคำนวณผลรวมของการโต้ตอบกำลังสองโดยใช้สูตรต่อไปนี้:
- ปฏิสัมพันธ์ SS = รวม SS – SS ปัจจัย 1 – SS ปัจจัย 2 – SS ภายใน
- การโต้ตอบ SS = 28.45975 – 0.00025 – 18.76475 – 8.684
- การโต้ตอบ SS = 1.01075
ขั้นตอนที่ 6: กรอกตาราง ANOVA ให้สมบูรณ์
สุดท้ายนี้ เราจะกรอกค่าจากตาราง ANOVA แบบสองทาง:
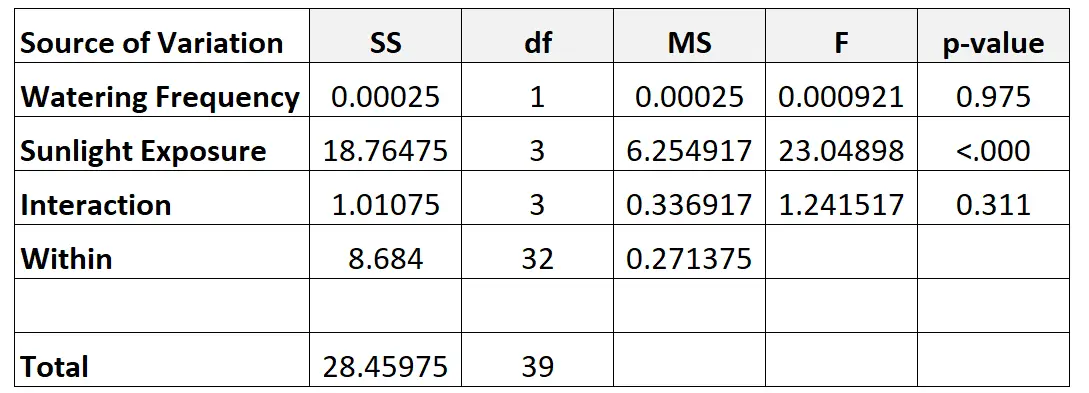
นี่คือวิธีที่เราคำนวณตัวเลขต่างๆ ในตาราง:
- df ความถี่ในการรดน้ำ: d-1 = 2-1 = 1
- df การสัมผัสกับแสงแดด: k-1 = 4-1 = 3
- dfปฏิสัมพันธ์ : (j-1)*(k-1) = 1*3 = 3
- df ใน : n – (j*k) = 40 – (2*4) = 32
- รวม df: n-1 = 40-1 = 39
- MS: SS/DF
- ความถี่ในการรดน้ำ F : ความถี่ในการรดน้ำ MS/MS ในร่ม
- F การสัมผัสกับแสงแดด : MS / MS การสัมผัสกับแสงแดดในอาคาร
- ปฏิสัมพันธ์ F : ปฏิสัมพันธ์ MS / MS ภายใน
- ความถี่ในการรดน้ำ p-value : ค่า p ซึ่งสอดคล้องกับค่า F 0.000921 โดยมีตัวเศษ df = 1 และตัวส่วน df = 32
- ปริมาณแสงแดด p-value : ค่า p ซึ่งสอดคล้องกับค่า F เท่ากับ 23.04898 โดยมีตัวเศษ df = 3 และตัวส่วน df = 32
- ปฏิสัมพันธ์ของค่า p : ค่า p ซึ่งสอดคล้องกับค่า F ของ 1.241517 โดยมีตัวเศษ df = 3 และตัวส่วน df = 32
หมายเหตุ #1: n = จำนวนการสังเกตทั้งหมด, j = จำนวนระดับความถี่ในการรดน้ำ, k = จำนวนระดับการรับแสงแดด
หมายเหตุ #2 : ค่า p ที่สอดคล้องกับค่า F คำนวณโดยใช้ เครื่องคำนวณการกระจายตัว F
ขั้นตอนที่ 7: ตีความผลลัพธ์
เราสามารถสังเกตสิ่งต่อไปนี้ได้จากตาราง ANOVA:
- ค่า p ของปฏิสัมพันธ์ระหว่างความถี่ในการรดน้ำและแสงแดดเท่ากับ 0.311 ซึ่งไม่มีนัยสำคัญทางสถิติที่ α = 0.05
- ค่า p ความถี่ในการรดน้ำเท่ากับ 0.975 ซึ่งไม่มีนัยสำคัญทางสถิติที่ α = 0.05
- ค่า p สำหรับการสัมผัสกับแสงแดดคือ <0.000 ซึ่งมีนัยสำคัญทางสถิติที่ α = 0.05
ผลลัพธ์เหล่านี้บ่งชี้ว่าแสงแดดเป็นปัจจัยเดียวที่มีผลกระทบที่มีนัยสำคัญทางสถิติต่อความสูงของพืช
และเนื่องจากไม่มีผลกระทบจากปฏิกิริยาใดๆ ผลของแสงแดดจึงสม่ำเสมอในแต่ละระดับของความถี่ในการรดน้ำ
พูดง่ายๆ ก็คือ ไม่ว่าต้นไม้จะรดน้ำทุกวันหรือทุกสัปดาห์ก็ไม่มีผลกระทบต่อแสงแดดที่ส่งผลต่อต้นไม้
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับ ANOVA:
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวด้วยตนเอง
วิธีการดำเนินการวัดความแปรปรวนซ้ำ ๆ ด้วยตนเอง
คู่มือฉบับสมบูรณ์: วิธีรายงานผลลัพธ์การวิเคราะห์ความแปรปรวนแบบสองทาง