วิธีการทดสอบ cramer-von mises ใน r (พร้อมตัวอย่าง)

การทดสอบ Cramer-Von Mises ใช้เพื่อพิจารณาว่าตัวอย่างมาจาก การกระจายตัวแบบปกติ หรือไม่

การทดสอบประเภทนี้มีประโยชน์ในการพิจารณาว่าชุดข้อมูลที่กำหนดมาจากการแจกแจงแบบปกติหรือไม่ ซึ่งเป็น สมมติฐานที่ใช้กันทั่วไป ในการทดสอบทางสถิติหลายอย่าง รวมถึง การถดถอย การวิเคราะห์ความแปรปรวน การทดสอบที และอื่นๆ อีกมากมาย ‘คนอื่น.

เราสามารถทำการทดสอบ Cramer-Von Mises ได้อย่างง่ายดายโดยใช้ฟังก์ชัน cvm.test() จากแพ็คเกจ goftest ใน R

ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้ในทางปฏิบัติ

ตัวอย่างที่ 1: การทดสอบ Cramer-Von Mises กับข้อมูลปกติ

รหัสต่อไปนี้แสดงวิธีดำเนินการทดสอบ Cramer-Von Mises บนชุดข้อมูลที่มีขนาดตัวอย่าง n=100:

 library (goftest)

#make this example reproducible
set. seeds (0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Cramer-Von Mises test for normality
cvm. test (data, ' pnorm ')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:data
omega2 = 0.078666, p-value = 0.7007

ค่า p ของการทดสอบกลายเป็น 0.7007 .

เนื่องจากค่านี้ไม่น้อยกว่า 0.05 เราจึงสามารถสรุปได้ว่าข้อมูลตัวอย่างมาจากประชากรที่มีการกระจายแบบปกติ

ผลลัพธ์นี้ไม่น่าประหลาดใจเนื่องจากเราสร้างข้อมูลตัวอย่างโดยใช้ฟังก์ชัน rnorm() ซึ่งสร้างค่าสุ่มจาก การแจกแจงแบบปกติมาตรฐาน

ที่เกี่ยวข้อง: คำแนะนำเกี่ยวกับ dnorm, pnorm, qnorm และ rnorm ใน R

นอกจากนี้เรายังสามารถสร้างฮิสโตแกรมเพื่อตรวจสอบด้วยสายตาว่าข้อมูลตัวอย่างมีการกระจายตามปกติ:

 hist(data, col=' steelblue ') 

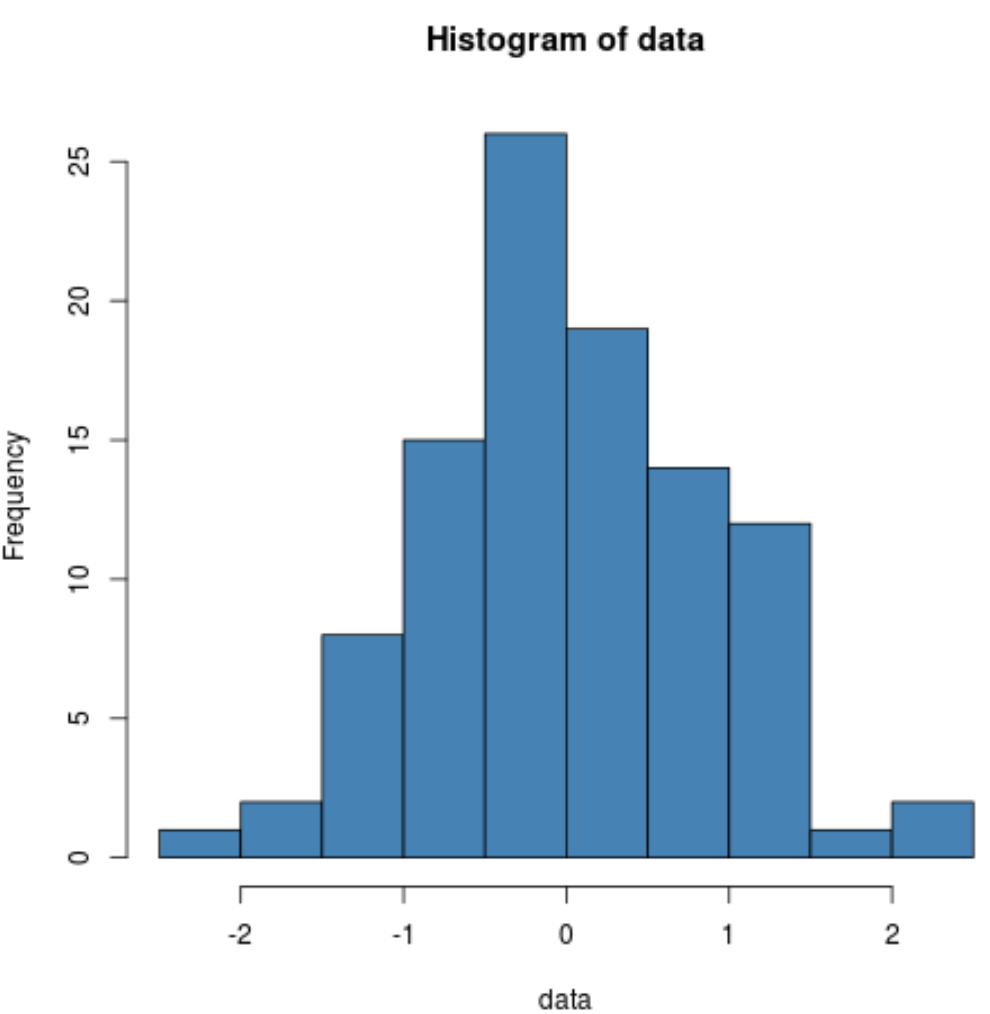
เราจะเห็นได้ว่าการแจกแจงนั้นค่อนข้างเป็นรูประฆังโดยมียอดอยู่ตรงกลางของการแจกแจง ซึ่งเป็นเรื่องปกติของข้อมูลที่แจกแจงแบบปกติ

ตัวอย่างที่ 2: การทดสอบ Cramer-Von Mises กับข้อมูลที่ไม่ปกติ

รหัสต่อไปนี้แสดงวิธีดำเนินการทดสอบ Cramer-Von Mises บนชุดข้อมูลที่มีขนาดตัวอย่าง 100 โดยค่าจะถูกสร้างขึ้นแบบสุ่มจาก การแจกแจงปัวซอง :

 library (goftest)

#make this example reproducible
set. seeds (0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Cramer-Von Mises test for normality
cvm. test (data, ' pnorm ')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:data
omega2 = 27.96, p-value < 2.2e-16

ค่า p ของการทดสอบมีค่าต่ำมาก

เนื่องจากค่านี้น้อยกว่า 0.05 เราจึงมีหลักฐานเพียงพอที่จะบอกว่าข้อมูลตัวอย่าง ไม่ได้ มาจากประชากรที่แจกแจงแบบปกติ

ผลลัพธ์นี้ไม่น่าประหลาดใจเนื่องจากเราสร้างข้อมูลตัวอย่างโดยใช้ฟังก์ชัน rpois() ซึ่งสร้างค่าสุ่มจากการแจกแจงแบบปัวซอง

ที่เกี่ยวข้อง: คำแนะนำเกี่ยวกับ dpois, ppois, qpois และ rpois ใน R

นอกจากนี้เรายังสามารถสร้างฮิสโตแกรมเพื่อให้เห็นว่าข้อมูลตัวอย่างไม่ได้กระจายตามปกติ:

 hist(data, col=' coral2 ') 

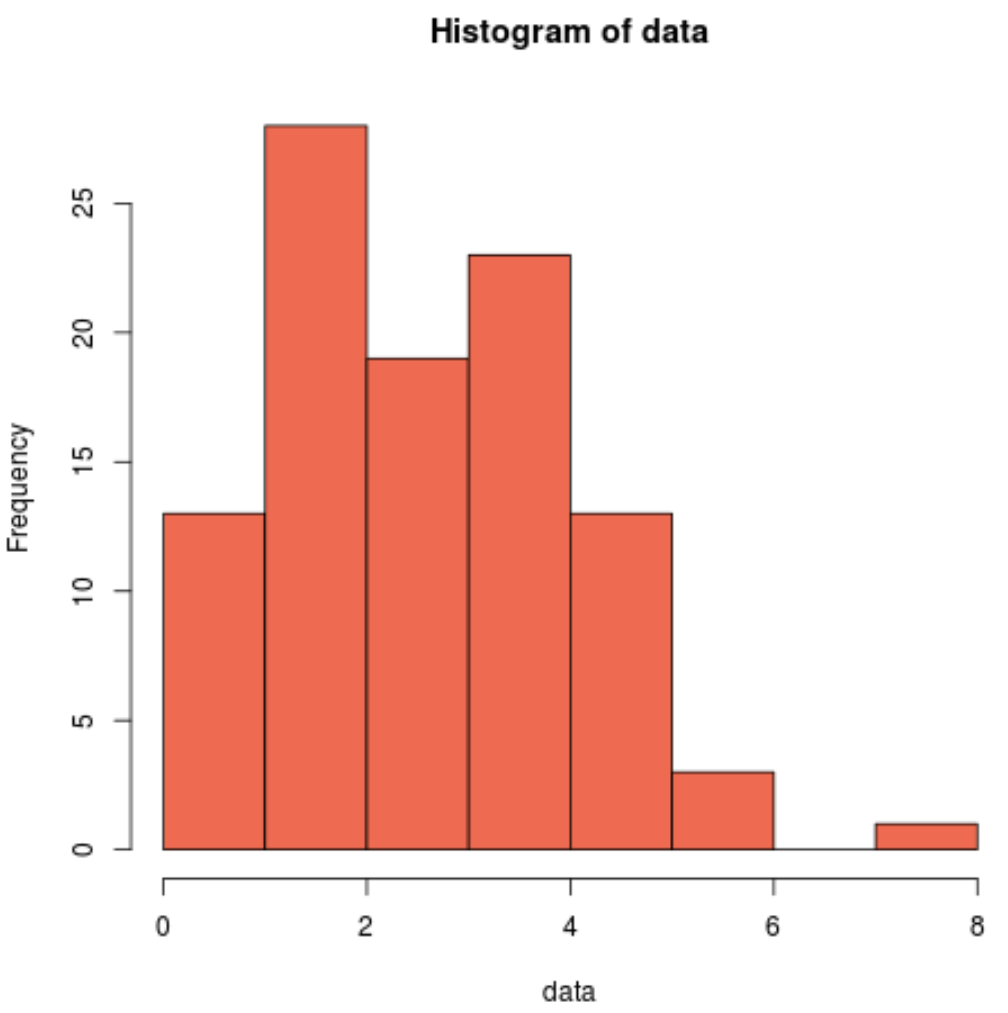
เราจะเห็นได้ว่าการแจกแจงนั้น เบ้ขวา และไม่มี “รูปทรงระฆัง” ทั่วไปที่เกี่ยวข้องกับการแจกแจงแบบปกติ

ดังนั้น ฮิสโตแกรมของเราจึงตรงกับผลลัพธ์ของการทดสอบ Cramer-Von Mises และยืนยันว่าข้อมูลตัวอย่างของเราไม่ได้มาจากการแจกแจงแบบปกติ

จะทำอย่างไรกับข้อมูลที่ไม่ปกติ

หากชุดข้อมูลที่กำหนด ไม่ได้ รับการแจกแจงตามปกติ เรามักจะดำเนินการแปลงอย่างใดอย่างหนึ่งต่อไปนี้เพื่อให้เป็นเรื่องปกติมากขึ้นได้:

1. การแปลงบันทึก: แปลงตัวแปรการตอบสนองจาก y เป็น log(y)

2. การแปลงรากที่สอง: แปลงตัวแปรตอบสนองจาก y เป็น √y

3. การแปลงรากที่สาม: แปลงตัวแปรการตอบสนองจาก y เป็น y ^1/3

โดยการดำเนินการแปลงเหล่านี้ โดยทั่วไปแล้วตัวแปรการตอบสนองจะประมาณค่าการแจกแจงแบบปกติ

โปรดดู บทช่วยสอนนี้ เพื่อดูวิธีดำเนินการแปลงเหล่านี้ในทางปฏิบัติ

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการทดสอบภาวะปกติอื่นๆ ใน R:

วิธีทำการทดสอบ Shapiro-Wilk ใน R
วิธีทำการทดสอบ Anderson-Darling ใน R
วิธีทำการทดสอบ Kolmogorov-Smirnov ใน R