วิธีการคำนวณ dfbetas ใน r
ในสถิติ เรามักต้องการทราบว่าสิ่งใดมีอิทธิพลต่อ การสังเกต ต่างๆ ในแบบจำลองการถดถอย
วิธีหนึ่งในการคำนวณอิทธิพลของการสังเกตคือการใช้หน่วยเมตริกที่เรียกว่า DFBETAS ซึ่งบอกเราถึงผลกระทบที่เป็นมาตรฐานต่อค่าสัมประสิทธิ์แต่ละค่าในการลบการสังเกตแต่ละรายการออก
ตัวชี้วัดนี้ทำให้เราทราบถึงอิทธิพลของการสังเกตแต่ละครั้งต่อการประมาณค่าสัมประสิทธิ์แต่ละรายการในแบบจำลองการถดถอยที่กำหนด
บทช่วยสอนนี้แสดงตัวอย่างทีละขั้นตอนของวิธีคำนวณและแสดงภาพ DFBETAS สำหรับการสังเกตแต่ละครั้งในแบบจำลองใน R
ขั้นตอนที่ 1: สร้างแบบจำลองการถดถอย
ขั้นแรก เราจะสร้าง โมเดลการถดถอยเชิงเส้นหลายตัว โดยใช้ชุดข้อมูล mtcars ที่สร้างไว้ใน R:
#fit a regression model model <- lm(mpg~disp+hp, data=mtcars) #view model summary summary(model) Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 30.735904 1.331566 23.083 < 2nd-16 *** available -0.030346 0.007405 -4.098 0.000306 *** hp -0.024840 0.013385 -1.856 0.073679 . --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.127 on 29 degrees of freedom Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09
ขั้นตอนที่ 2: คำนวณ DFBETAS สำหรับการสังเกตแต่ละครั้ง
ต่อไป เราจะใช้ฟังก์ชัน dfbetas() ในตัวเพื่อคำนวณค่า DFBETAS สำหรับการสังเกตแต่ละครั้งในแบบจำลอง:
#calculate DFBETAS for each observation in the model dfbetas <- as . data . frame (dfbetas(model)) #display DFBETAS for each observation dfbetas (Intercept) disp hp Mazda RX4 -0.1174171253 0.030760632 1.748143e-02 Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02 Datsun 710 -0.1694989349 0.086630144 -3.332781e-05 Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02 Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01 Valiant -0.1711908285 -0.139135639 1.829038e-01 Duster 360 -0.0312338677 -0.005356209 3.581378e-02 Merc 240D -0.0312259577 -0.010409922 2.433256e-02 Merc 230 -0.0865872595 0.016428917 2.287867e-02 Merc 280 -0.1560683502 0.078667906 -1.911180e-02 Merc 280C -0.2254489597 0.113639937 -2.760800e-02 Merc 450SE 0.0022844093 0.002966155 -2.855985e-02 Merc 450SL 0.0009062022 0.001176644 -1.132941e-02 Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02 Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02 Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02 Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02 Fiat 128 0.5720358325 -0.181104179 -1.265475e-01 Honda Civic 0.3490872162 -0.053660545 -1.326422e-01 Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01 Toyota Corona -0.2181110386 0.101336902 5.945352e-03 Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02 AMC Javelin -0.0406785103 -0.141711468 1.074514e-01 Camaro Z28 0.0390139262 0.012846225 -5.031588e-02 Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01 Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02 Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02 Lotus Europa 0.3444562478 -0.402678927 2.135224e-01 Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01 Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01 Maserati Bora -0.3436265545 -0.511285637 7.319066e-01 Volvo 142E -0.1784974091 0.132692956 -4.433915e-02
สำหรับการสังเกตแต่ละครั้ง เราจะเห็นความแตกต่างในการประมาณค่าสัมประสิทธิ์สำหรับจุดเริ่มต้น ตัวแปร disp และตัวแปร hp ที่เกิดขึ้นเมื่อเราลบการสังเกตนั้นออก
โดยทั่วไป เราพิจารณาว่าการสังเกตมีอิทธิพลอย่างมากต่อการประมาณค่าสัมประสิทธิ์ที่กำหนด หากมีค่า DBETAS มากกว่าเกณฑ์ 2/√ n โดยที่ n คือจำนวนการสังเกต
ในตัวอย่างนี้ เกณฑ์จะเป็น 0.3535534 :
#find number of observations n <- nrow (mtcars) #calculate DFBETAS threshold value thresh <- 2/ sqrt (n) thresh [1] 0.3535534
ขั้นตอนที่ 3: แสดงภาพ DFBETAS
สุดท้ายนี้ เราสามารถสร้างแผนเพื่อแสดงภาพค่า DFBETAS สำหรับการสังเกตแต่ละครั้งและสำหรับตัวทำนายแต่ละตัวในแบบจำลอง:
#specify 2 rows and 1 column in plotting region by(mfrow=c(2,1)) #plot DFBETAS for disp with threshold lines plot(dfbetas$disp, type=' h ') abline(h = thresh, lty = 2) abline(h = -thresh, lty = 2) #plot DFBETAS for hp with threshold lines plot(dfbetas$hp, type=' h ') abline(h = thresh, lty = 2) abline(h = -thresh, lty = 2)
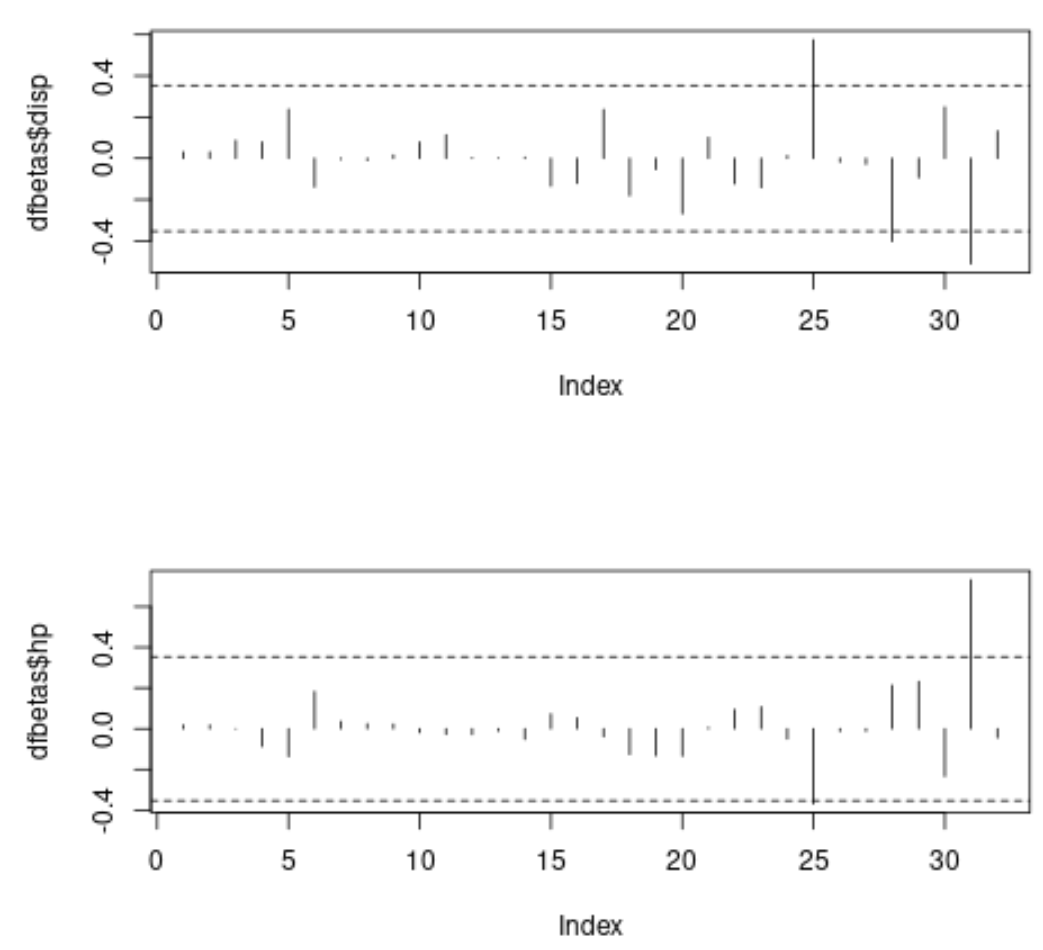
ในแต่ละพล็อต แกน x จะแสดงดัชนีของการสังเกตแต่ละครั้งในชุดข้อมูล และค่า y จะแสดง DFBETAS ที่สอดคล้องกันสำหรับการสังเกตแต่ละครั้งและตัวทำนายแต่ละตัว
บนพล็อตแรก เราจะเห็นว่าการสังเกตสามครั้งเกินค่าขีดจำกัดสัมบูรณ์ที่ 0.3535534 และบนพล็อตที่สอง เราจะเห็นว่าการสังเกตสองครั้งเกินค่าขีดจำกัดสัมบูรณ์
เราอาจเลือกที่จะศึกษาข้อสังเกตเหล่านี้อย่างใกล้ชิดมากขึ้นเพื่อพิจารณาว่าสิ่งเหล่านี้มีอิทธิพลเกินสมควรต่อการประมาณค่าสัมประสิทธิ์แบบจำลองหรือไม่
แหล่งข้อมูลเพิ่มเติม
วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน R
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
วิธีการคำนวณสถิติเลเวอเรจใน R
วิธีการคำนวณ DFFITS ใน R