วิธีทำการทดสอบ t-test โดยมีความแปรปรวนไม่เท่ากันใน excel

การทดสอบทีแบบสองตัวอย่าง ใช้เพื่อพิจารณาว่า ค่าเฉลี่ยของประชากรทั้งสอง เท่ากันหรือไม่

มีตัวอย่างการทดสอบ t-test สองเวอร์ชันที่คุณสามารถใช้ได้:

• ทดสอบด้วยความแปรปรวนเท่ากัน
• ทดสอบทีโดยมีความแปรปรวนไม่เท่ากัน

เราใช้การทดสอบทีโดยมีความแปรปรวนไม่เท่ากัน เมื่อความแปรปรวนของทั้งสองตัวอย่างไม่เท่ากัน

วิธีที่ง่ายที่สุดในการพิจารณาว่าความแปรปรวนระหว่างตัวอย่างทั้งสองเท่ากันหรือไม่คือการใช้ กฎความแปรปรวนทั่วไป

ตามกฎทั่วไป หากอัตราส่วนของความแปรปรวนที่ใหญ่ที่สุดต่อความแปรปรวนที่น้อยที่สุดน้อยกว่า 4 เราสามารถสรุปได้ว่าความแปรปรวนนั้นมีค่าเท่ากันโดยประมาณ

มิฉะนั้น หากอัตราส่วนเท่ากับหรือมากกว่า 4 จะถือว่าความแปรปรวนไม่เท่ากัน

ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีดำเนินการทดสอบทีสองตัวอย่างโดยมีความแปรปรวนไม่เท่ากันใน Excel

ขั้นตอนที่ 1: ป้อนข้อมูล

สมมติว่าเราต้องการพิจารณาว่าวิธีการศึกษาสองวิธีที่แตกต่างกันทำให้คะแนนสอบเฉลี่ยของนักศึกษาในมหาวิทยาลัยที่กำหนดแตกต่างกันหรือไม่

เราสุ่มตัวอย่างนักเรียนจำนวน 20 คน เพื่อใช้วิธีการเรียนแต่ละวิธีและบันทึกผลการสอบ:

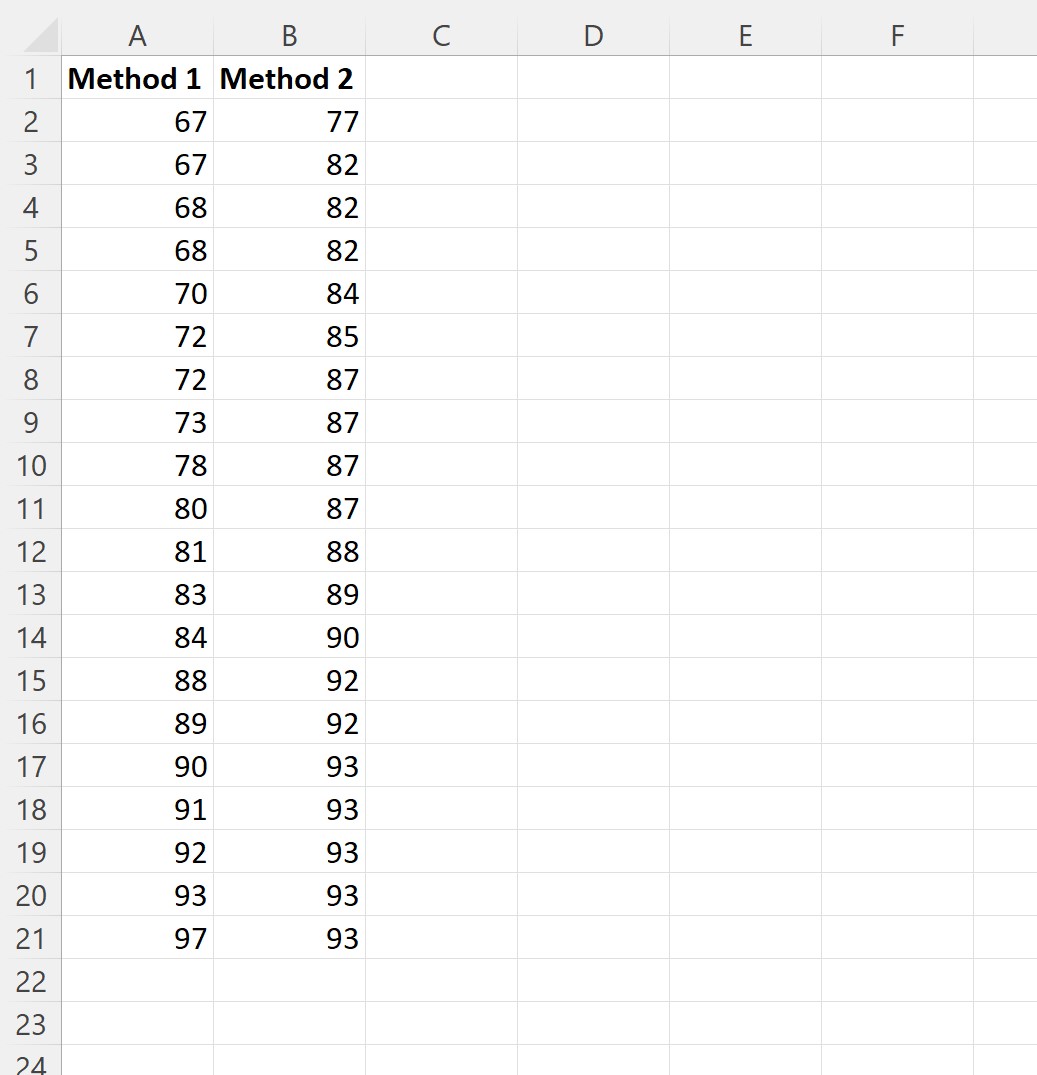
ขั้นตอนที่ 2: กำหนดความแปรปรวนที่เท่ากันหรือไม่เท่ากัน

จากนั้นเราสามารถคำนวณอัตราส่วนของความแปรปรวนตัวอย่างได้:

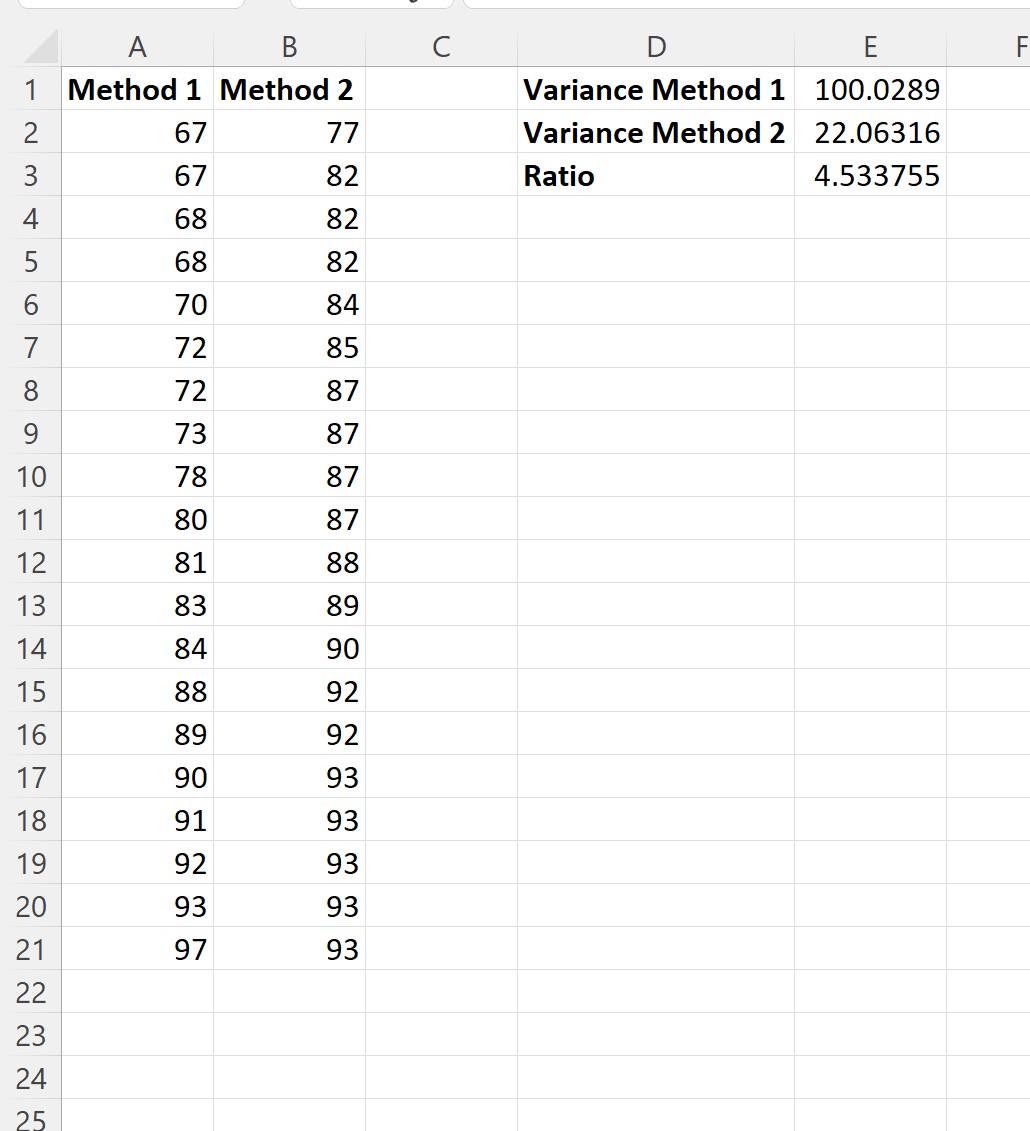
นี่คือสูตรที่เราพิมพ์ในแต่ละเซลล์:

• เซลล์ E1: =VAR.S(A2:A21)
• เซลล์ E2: =VAR.S(B2:B21)
• เซลล์ E3: =E1/E2

เราจะเห็นว่าอัตราส่วนของความแปรปรวนตัวอย่างที่ใหญ่ที่สุดต่อความแปรปรวนตัวอย่างที่น้อยที่สุดคือ 4.533755

ค่านี้มากกว่าหรือเท่ากับ 4 เราถือว่าความแปรปรวนระหว่างสองตัวอย่างไม่เท่ากัน

ขั้นตอนที่ 3: ทำการทดสอบทีสองตัวอย่างโดยมีความแปรปรวนไม่เท่ากัน

ต่อไป เราสามารถทำการทดสอบค่าทีสองตัวอย่างโดยมีความแปรปรวนไม่เท่ากันเพื่อพิจารณาว่าคะแนนสอบเฉลี่ยระหว่างทั้งสองตัวอย่างเท่ากันหรือไม่

เมื่อต้องการทำเช่นนี้ คลิกแท็บ ข้อมูล ใน Ribbon ด้านบน จากนั้นคลิกปุ่ม การวิเคราะห์ข้อมูล ในกลุ่ม วิเคราะห์ :

หากคุณไม่เห็นปุ่มนี้ คุณต้อง ติดตั้ง Data Analysis Toolpak ฟรีใน Excel ก่อน

ในหน้าต่างใหม่ที่ปรากฏขึ้น คลิก T-test: Two-Sample Assuming Unequal Variances จากนั้นคลิก OK :

ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้กรอกข้อมูลต่อไปนี้ จากนั้นคลิก OK :

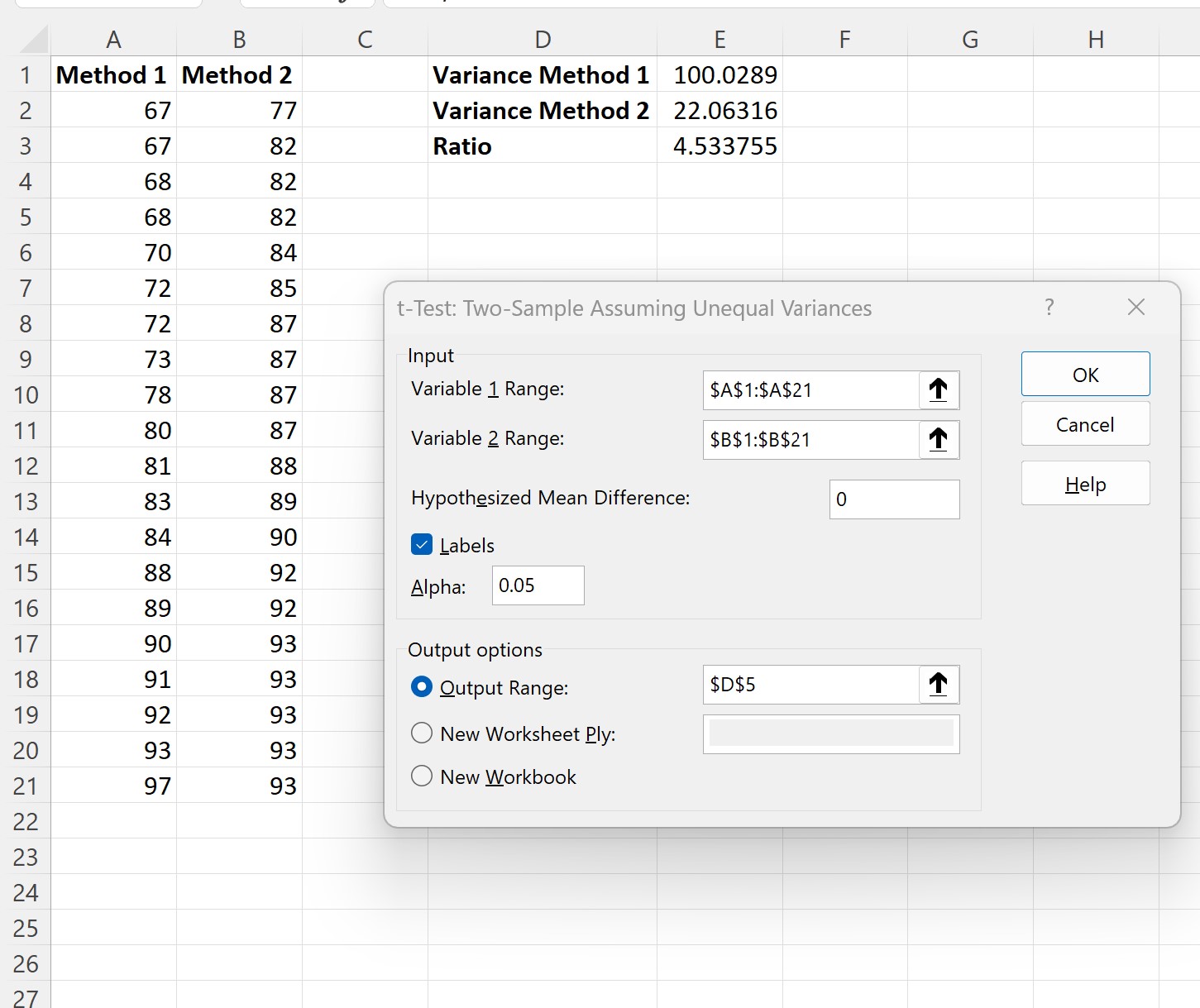
เมื่อคุณคลิก ตกลง ผลลัพธ์ของตัวอย่างการทดสอบทีทั้งสองรายการจะปรากฏขึ้น:

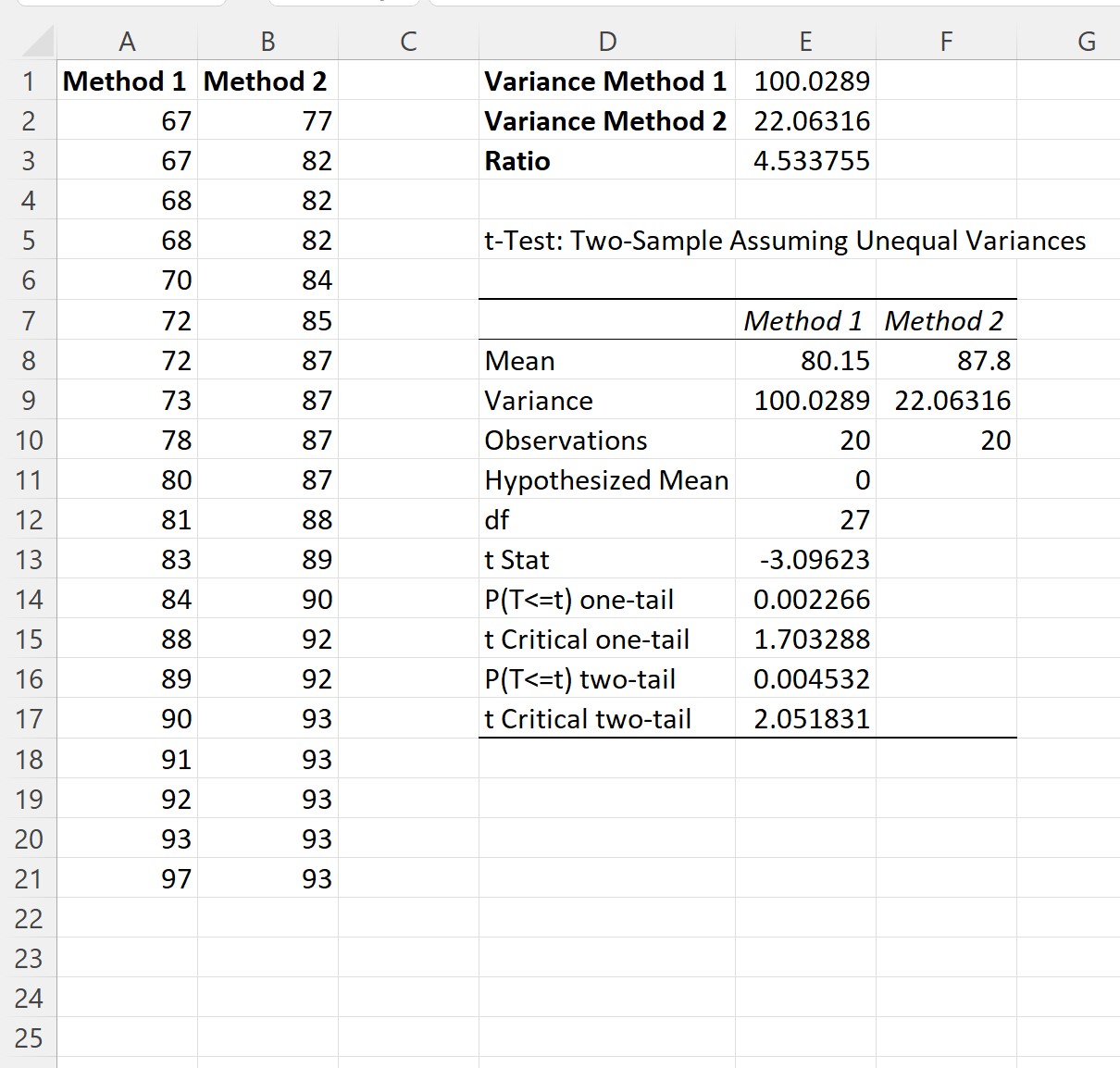
ขั้นตอนที่ 4: ตีความผลลัพธ์

จากผลลัพธ์เราจะเห็นได้ว่า:

• คะแนนสอบเฉลี่ยวิธีที่ 1 เท่ากับ 80.15
• คะแนนสอบเฉลี่ยวิธีที่ 2 เท่ากับ 87.8
• สถิติการทดสอบทีคือ -3.09623
• ค่า p แบบสองด้านที่สอดคล้องกันคือ 0.004532

เนื่องจากค่า p นี้น้อยกว่า 0.05 เราจึงสามารถสรุปได้ว่าคะแนนสอบเฉลี่ยระหว่างวิธีการศึกษาทั้งสองวิธีมีความแตกต่างอย่างมีนัยสำคัญทางสถิติ

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้อธิบายวิธีการทำงานทั่วไปอื่นๆ ใน Excel:

วิธีดำเนินการทดสอบทีตัวอย่างเดียวใน Excel
วิธีดำเนินการทดสอบตัวอย่างแบบจับคู่ใน Excel
วิธีดำเนินการหนึ่งตัวอย่างและการทดสอบ Z สองตัวอย่างใน Excel