วิธีสร้าง qq plot ใน ggplot2 (พร้อมตัวอย่าง)

พล็อต QQ ย่อมาจาก “ควอนไทล์-ควอนไทล์” ใช้เพื่อประเมินว่าชุดข้อมูลอาจมาจากการแจกแจงทางทฤษฎีหรือไม่

ในกรณีส่วนใหญ่ การลงจุดประเภทนี้ใช้เพื่อพิจารณาว่าชุดข้อมูลเป็นไปตามการแจกแจงแบบปกติหรือไม่

หากข้อมูลมีการกระจายตามปกติ จุดบนพล็อต QQ จะอยู่บนเส้นทแยงมุม

ในทางกลับกัน หากจุดเบี่ยงเบนไปจากเส้นทแยงมุมอย่างมีนัยสำคัญ ข้อมูลก็มีแนวโน้มที่จะกระจายตามปกติน้อยลง

หากต้องการสร้างพล็อต QQ ใน ggplot2 คุณสามารถใช้ฟังก์ชัน stat_qq() และ stat_qq_line() ได้ดังต่อไปนี้:

 library (ggplot2)

ggplot(df, aes(sample=y)) +
  stat_qq() + 
  stat_qq_line()

ตัวอย่างต่อไปนี้แสดงวิธีใช้ไวยากรณ์นี้เพื่อสร้างพล็อต QQ ในสองสถานการณ์ที่แตกต่างกัน

ตัวอย่างที่ 1: พล็อต QQ สำหรับข้อมูลปกติ

รหัสต่อไปนี้แสดงวิธีสร้างชุดข้อมูลที่กระจายแบบปกติด้วย การสังเกต 200 ครั้ง และสร้างพล็อต QQ สำหรับชุดข้อมูลใน R:

 library (ggplot2)

#make this example reproducible
set. seeds (1)

#create some fake data that follows a normal distribution
df <- data. frame (y=rnorm(200))

#create QQ plot
ggplot(df, aes(sample=y)) +
  stat_qq() + 
  stat_qq_line()

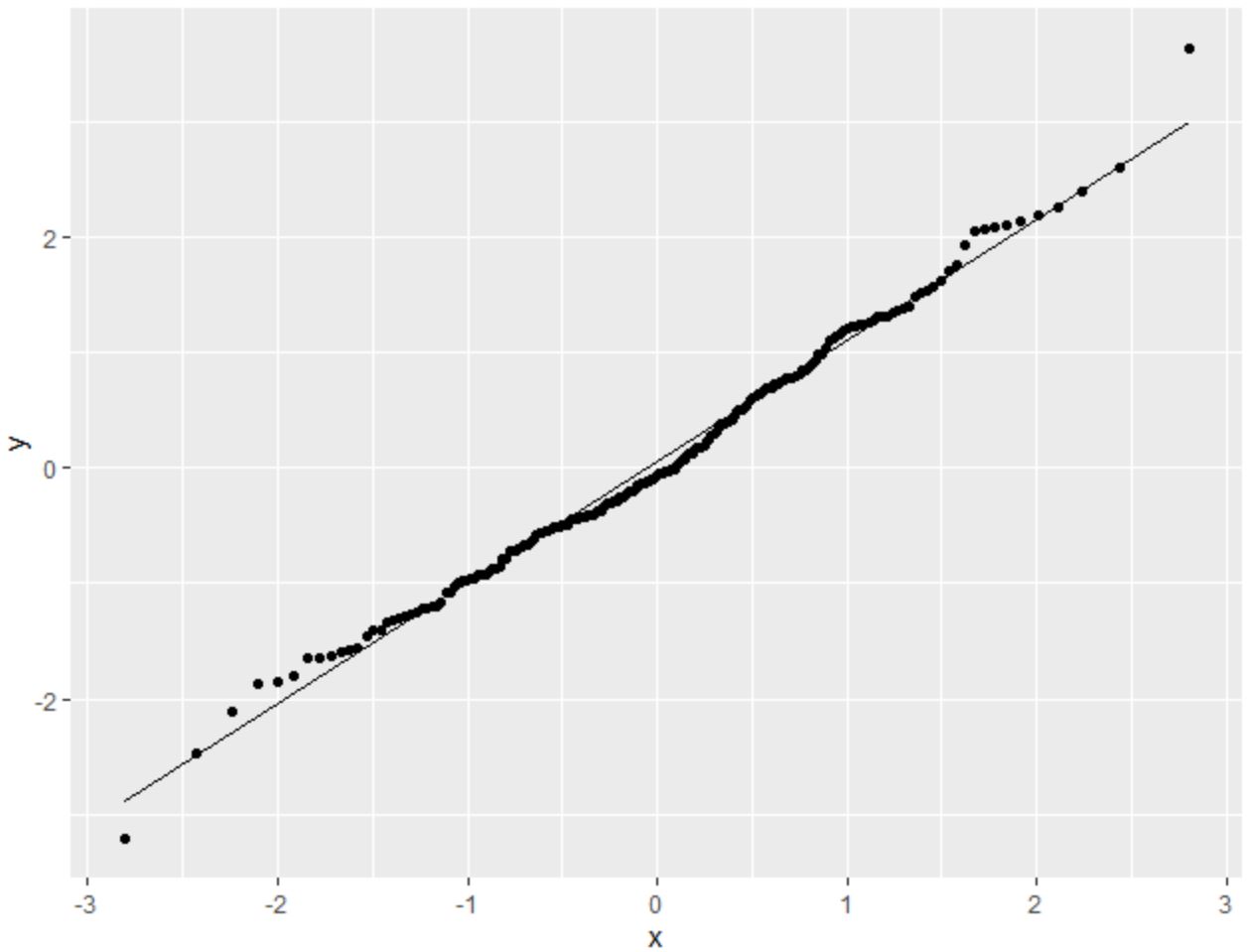
เราจะเห็นได้ว่าจุดต่างๆ มักจะอยู่ตามแนวเส้นทแยงมุมตรงโดยมีการเบี่ยงเบนเล็กน้อยตามหางแต่ละข้าง

จากกราฟนี้ เราจะถือว่าชุดข้อมูลนี้มีการกระจายตามปกติ

โปรดทราบว่าเรายังสามารถใช้อาร์กิวเมนต์สีและขนาดเพื่อเปลี่ยนสีและขนาดของจุดในโครงเรื่องได้หากเราต้องการ:

 library (ggplot2)

#make this example reproducible
set. seeds (1)

#create some fake data that follows a normal distribution
df <- data. frame (y=rnorm(200))

#create QQ plot
ggplot(df, aes(sample=y)) +
  stat_qq(size= 2.5 , color=' red ') + 
  stat_qq_line() 

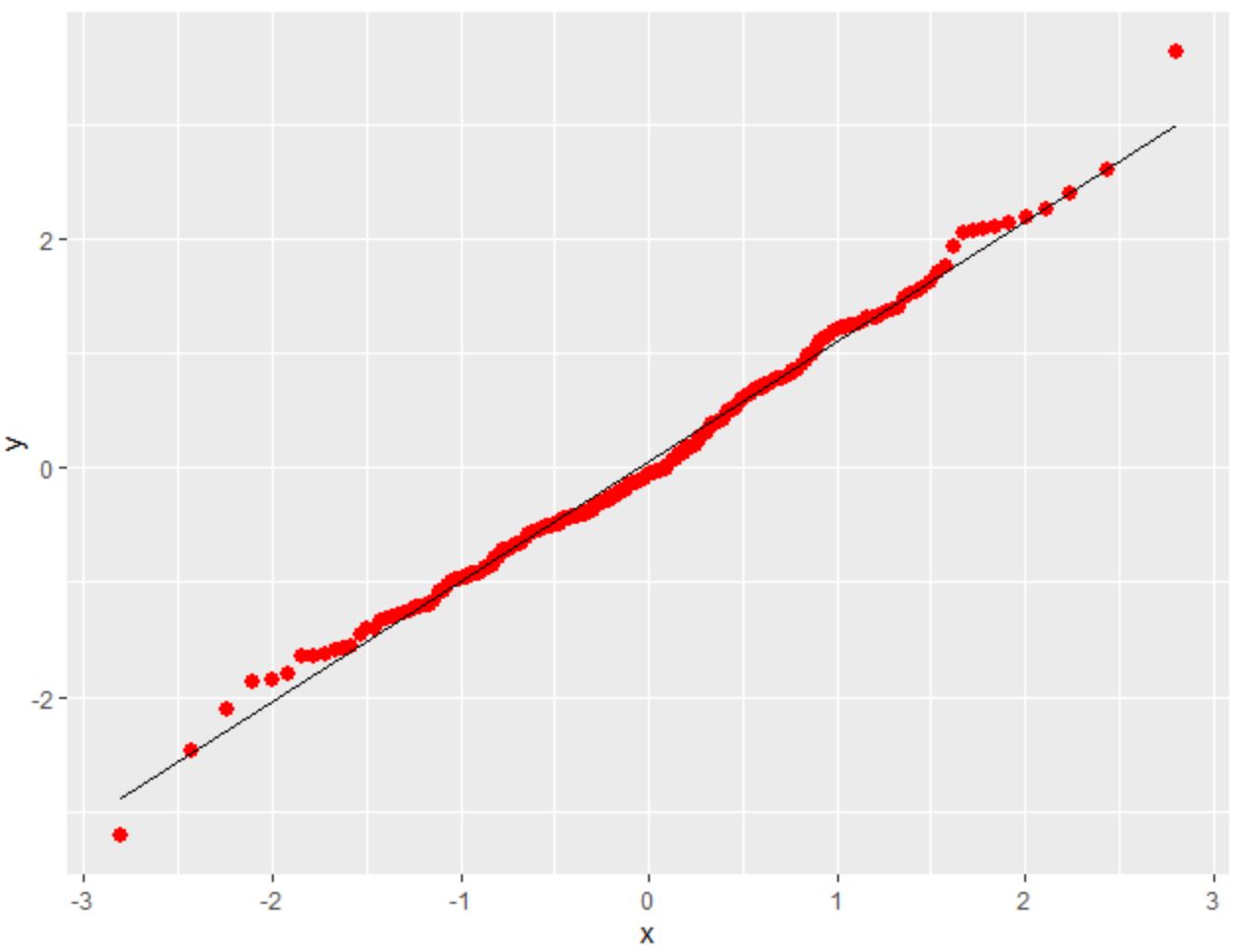
ตัวอย่างที่ 2: พล็อต QQ สำหรับข้อมูลที่ไม่ปกติ

รหัสต่อไปนี้แสดงวิธีสร้างพล็อต QQ สำหรับชุดข้อมูลที่ตามหลังการแจกแจงแบบเอ็กซ์โปเนนเชียลด้วยการสังเกต 200 ครั้ง:

 #make this example reproducible
set. seeds (1)

#create some fake data that follows an exponential distribution
df <- data. frame (y=rexp( 200 , rate= 3 ))

#create QQ plot
ggplot(df, aes(sample=y)) +
  stat_qq() + 
  stat_qq_line()

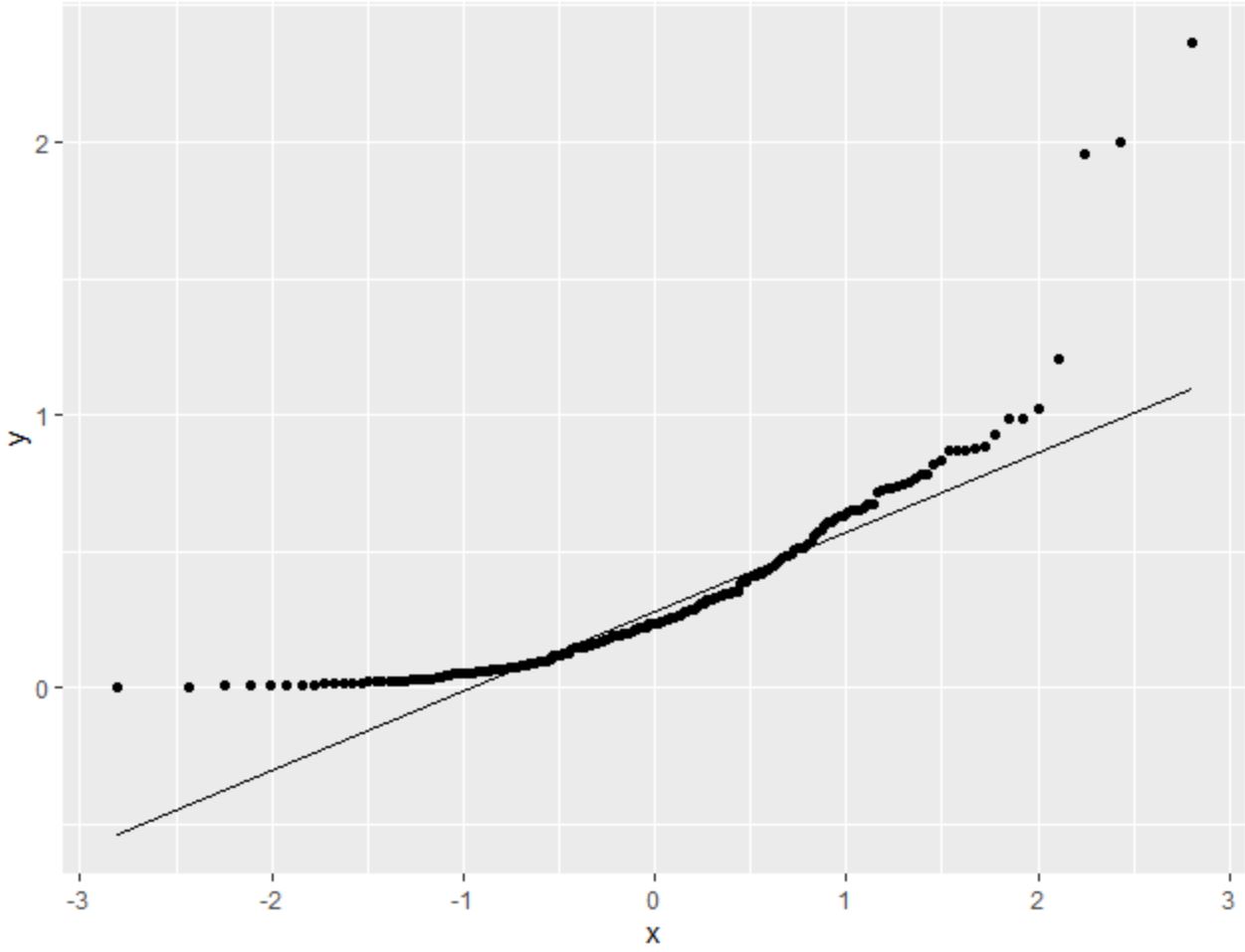
เราเห็นว่าจุดเบี่ยงเบนไปจากเส้นทแยงมุมมาก สิ่งนี้แสดงให้เห็นอย่างชัดเจนว่าชุดข้อมูลไม่ได้กระจายตามปกติ

สิ่งนี้น่าจะสมเหตุสมผลเนื่องจากเราระบุว่าข้อมูลควรเป็นไปตามการแจกแจงแบบเอ็กซ์โพเนนเชียล

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ ใน ggplot2:

วิธีพล็อตหลายบรรทัดใน ggplot2
วิธีการพล็อตค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานใน ggplot2
วิธีเปลี่ยนสีเส้นใน ggplot2