วิธีดำเนินการถดถอยเชิงเส้นใน google ชีต

การถดถอยเชิงเส้น เป็นวิธีการที่สามารถใช้ในการหาปริมาณความสัมพันธ์ระหว่าง ตัวแปรอธิบาย ตั้งแต่หนึ่งตัวขึ้นไปกับ ตัวแปรตอบสนอง

เราใช้การถดถอยเชิงเส้นอย่างง่ายเมื่อมีตัวแปรอธิบายเพียงตัวแปรเดียวและการถดถอยเชิงเส้นหลายตัวเมื่อมีตัวแปรอธิบายสองตัวขึ้นไป

การถดถอยทั้งสองประเภทสามารถทำได้โดยใช้ฟังก์ชัน LINEST() ของ Google ชีต ซึ่งใช้ไวยากรณ์ต่อไปนี้

LINEST (known_data_y,known_data_x, คำนวณ_b, รายละเอียด)

ทอง:

• known_data_y: อาร์เรย์ของค่าการตอบสนอง
• known_data_x: ตารางค่าอธิบาย
• Calculator_B: ระบุว่าจะคำนวณจุดตัดแกนหรือไม่ นี่เป็น TRUE โดยค่าเริ่มต้น และเราปล่อยไว้อย่างนั้นเพื่อการถดถอยเชิงเส้น
• รายละเอียด: ระบุว่าจะให้สถิติการถดถอยเพิ่มเติมนอกเหนือจากความชันและจุดตัดแกนหรือไม่ นี่เป็น FALSE ตามค่าเริ่มต้น แต่เราจะระบุว่าเป็นจริงในตัวอย่างของเรา

ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้ในทางปฏิบัติ

การถดถอยเชิงเส้นอย่างง่ายใน Google ชีต

สมมติว่าเราต้องการเข้าใจความสัมพันธ์ระหว่าง ชั่วโมงเรียน กับ ผลการสอบ กำลังศึกษาเพื่อสอบและเกรดที่ได้รับจากการสอบ

ในการสำรวจความสัมพันธ์นี้ เราสามารถทำการถดถอยเชิงเส้นอย่างง่ายโดยใช้ ชั่วโมงที่ศึกษา เป็นตัวแปรอธิบาย และ ใช้คะแนนสอบ เป็นตัวแปรตอบสนอง

ภาพหน้าจอต่อไปนี้แสดงวิธีการถดถอยเชิงเส้นอย่างง่ายโดยใช้ชุดข้อมูลของนักเรียน 20 คน โดยใช้สูตรต่อไปนี้ในเซลล์ D2:

= เส้น ( B2:B21 , A2:A21 , TRUE , TRUE )

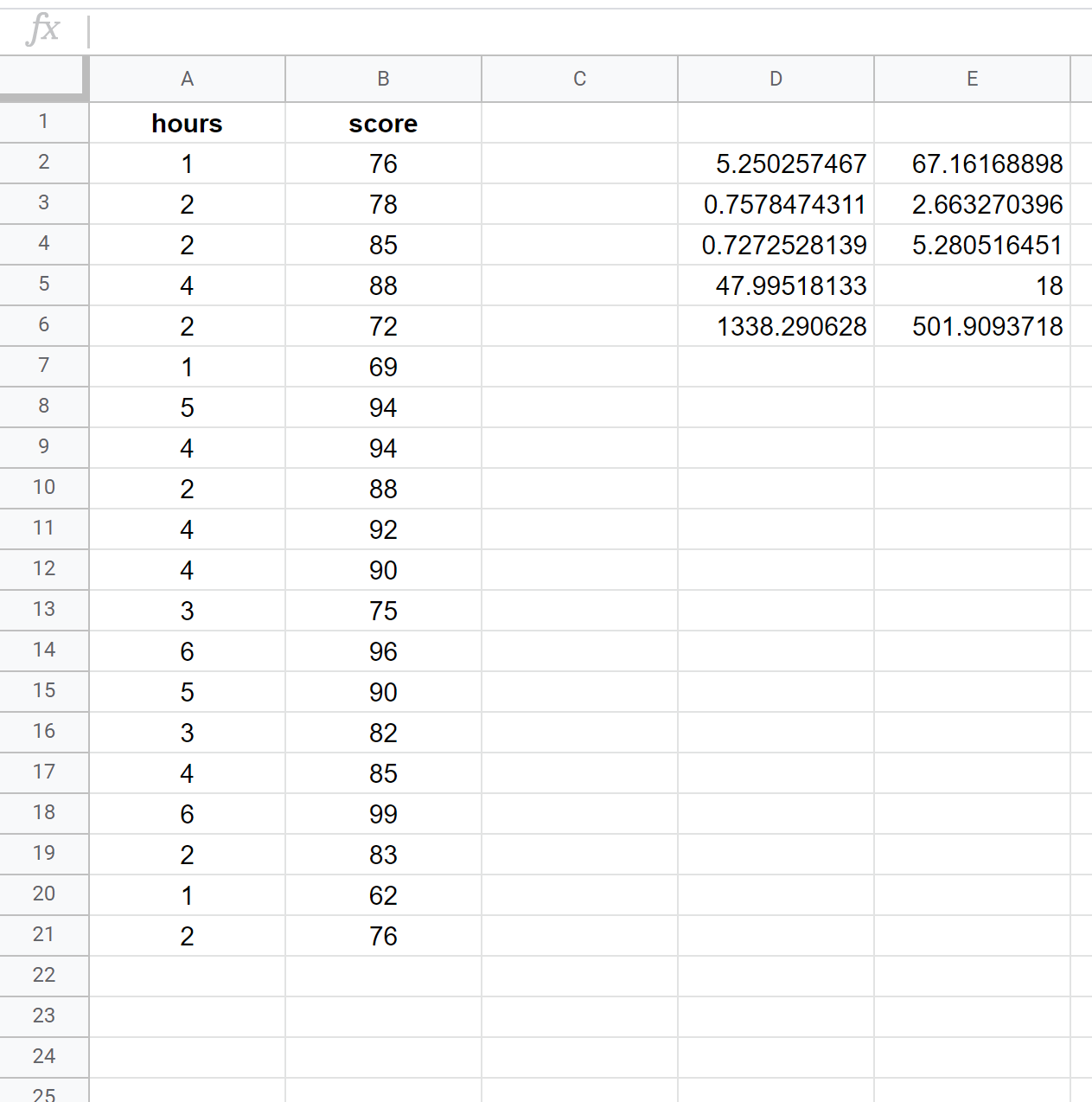
ภาพหน้าจอต่อไปนี้ให้คำอธิบายประกอบสำหรับเอาต์พุต:

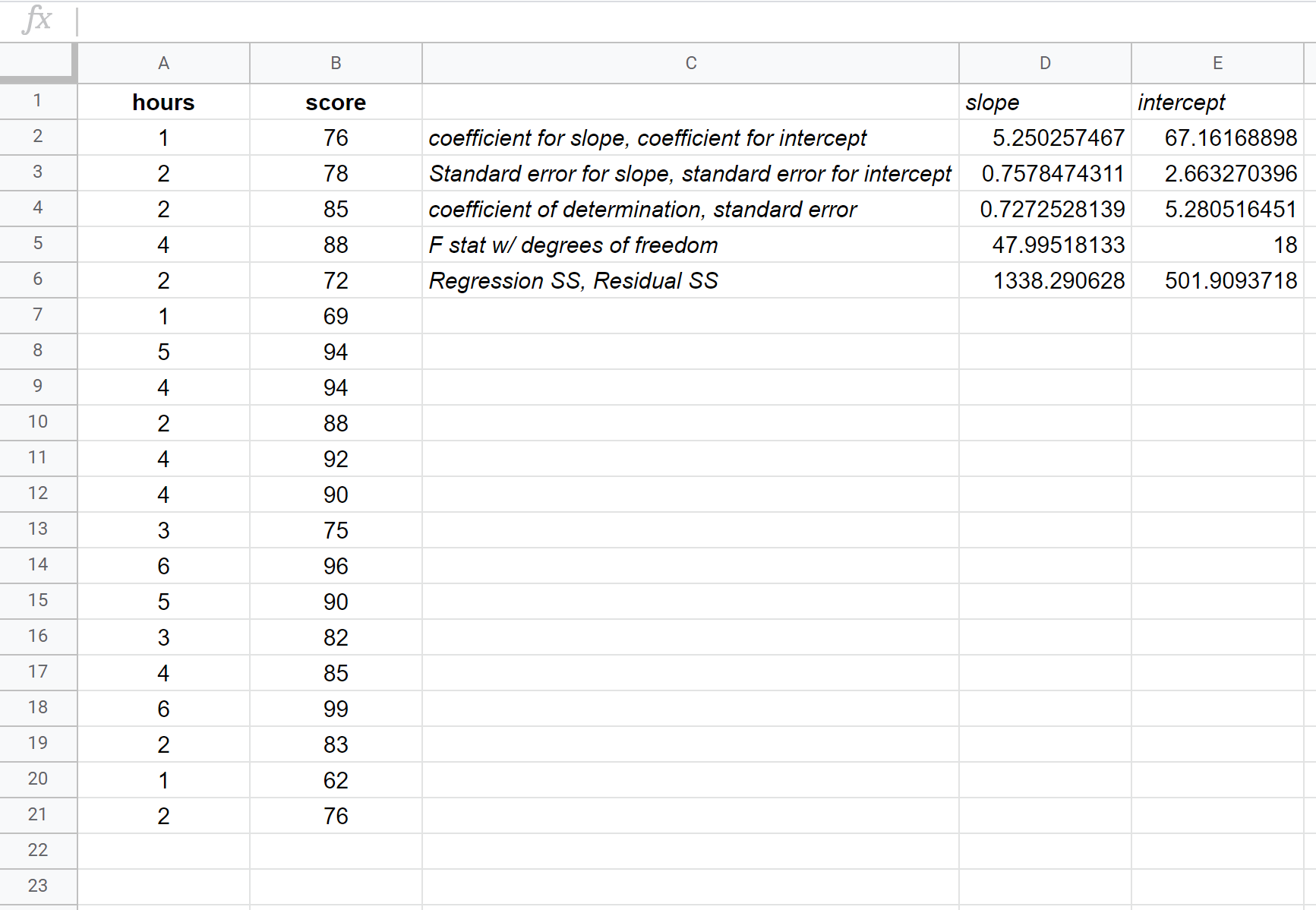
ต่อไปนี้คือวิธีตีความตัวเลขที่เกี่ยวข้องมากที่สุดในผลลัพธ์:

อาร์ สแควร์: 0.72725 . นี่เรียกว่าสัมประสิทธิ์การตัดสินใจ เป็นสัดส่วนของความแปรปรวนในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรอธิบาย ในตัวอย่างนี้ สามารถอธิบายความแปรผันของคะแนนสอบประมาณ 72.73% ด้วยจำนวนชั่วโมงที่เรียน

ข้อผิดพลาดมาตรฐาน: 5.2805 นี่คือระยะห่างเฉลี่ยระหว่างค่าที่สังเกตได้กับเส้นถดถอย ในตัวอย่างนี้ ค่าที่สังเกตได้เบี่ยงเบนโดยเฉลี่ย 5.2805 หน่วยจากเส้นถดถอย

ค่าสัมประสิทธิ์: ค่าสัมประสิทธิ์ให้ตัวเลขที่จำเป็นในการเขียนสมการการถดถอยโดยประมาณ ในตัวอย่างนี้ สมการการถดถอยโดยประมาณคือ:

คะแนนสอบ = 67.16 + 5.2503*(ชั่วโมง)

เราตีความค่าสัมประสิทธิ์ชั่วโมงว่า ในแต่ละชั่วโมงที่เรียนเพิ่มเติม คะแนนสอบควรเพิ่มขึ้นโดยเฉลี่ย 5.2503 เราตีความค่าสัมประสิทธิ์ของการสกัดกั้นว่าคะแนนสอบที่คาดหวังสำหรับนักเรียนที่เรียนเป็นศูนย์ชั่วโมงคือ 67.16

เราสามารถใช้สมการการถดถอยโดยประมาณนี้เพื่อคำนวณคะแนนสอบที่คาดหวังสำหรับนักเรียน โดยพิจารณาจากจำนวนชั่วโมงเรียน เช่น นักเรียนที่เรียน 3 ชั่วโมง ควรได้คะแนนสอบ 82.91 :

คะแนนสอบ = 67.16 + 5.2503*(3) = 82.91

การถดถอยเชิงเส้นพหุคูณใน Google ชีต

สมมติว่าเราต้องการทราบว่าจำนวนชั่วโมงในการเรียนและจำนวนการสอบเตรียมสอบส่งผลต่อเกรดที่นักเรียนได้รับในการสอบเข้าวิทยาลัยบางประเภทหรือไม่

ในการสำรวจความสัมพันธ์นี้ เราสามารถทำการถดถอยเชิงเส้นพหุคูณโดยใช้ ชั่วโมงการศึกษา และ การสอบเตรียมการที่ใช้ เป็นตัวแปรอธิบาย และ ผลการสอบ เป็นตัวแปรตอบสนอง

ภาพหน้าจอต่อไปนี้แสดงวิธีการถดถอยเชิงเส้นพหุคูณโดยใช้ชุดข้อมูลของนักเรียน 20 คน โดยใช้สูตรต่อไปนี้ในเซลล์ E2:

= ขวา ( C2:C21 , A2:B21 , TRUE , TRUE )

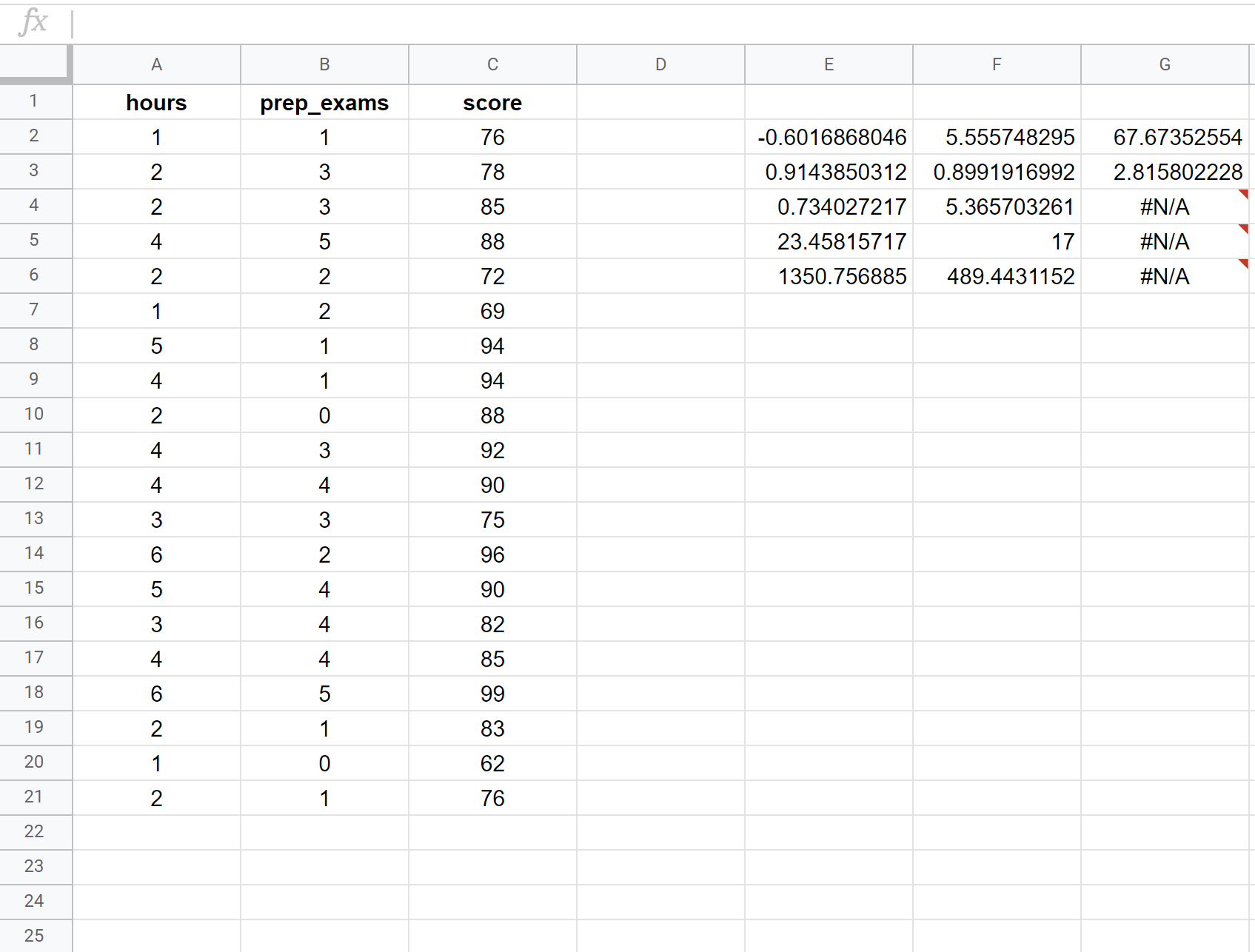
ต่อไปนี้คือวิธีตีความตัวเลขที่เกี่ยวข้องมากที่สุดในผลลัพธ์:

อาร์ สแควร์: 0.734 . นี่เรียกว่าสัมประสิทธิ์การตัดสินใจ เป็นสัดส่วนของความแปรปรวนของตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรอธิบาย ในตัวอย่างนี้ 73.4% ของการเปลี่ยนแปลงของคะแนนสอบอธิบายได้จากจำนวนชั่วโมงที่เรียนและจำนวนการสอบเพื่อเตรียมสอบ

ข้อผิดพลาดมาตรฐาน: 5.3657 นี่คือระยะห่างเฉลี่ยระหว่างค่าที่สังเกตได้กับเส้นถดถอย ในตัวอย่างนี้ ค่าที่สังเกตได้เบี่ยงเบนโดยเฉลี่ย 5.3657 หน่วยจากเส้นถดถอย

สมการการถดถอยโดยประมาณ: เราสามารถใช้สัมประสิทธิ์จากเอาต์พุตแบบจำลองเพื่อสร้างสมการการถดถอยโดยประมาณต่อไปนี้:

คะแนนสอบ = 67.67 + 5.56*(ชม.) – 0.60*(สอบเตรียมอุดมศึกษา)

เราสามารถใช้สมการการถดถอยโดยประมาณนี้เพื่อคำนวณคะแนนสอบที่คาดหวังสำหรับนักเรียน โดยพิจารณาจากจำนวนชั่วโมงเรียนและจำนวนข้อสอบฝึกหัดที่พวกเขาทำ เช่น นักเรียนที่เรียน 3 ชั่วโมงและสอบเตรียมสอบควรได้เกรด 83.75 :

คะแนนสอบ = 67.67 + 5.56*(3) – 0.60*(1) = 83.75

แหล่งข้อมูลเพิ่มเติม

บทแนะนำต่อไปนี้จะอธิบายวิธีทำงานทั่วไปอื่นๆ ใน Google ชีต

วิธีดำเนินการถดถอยพหุนามใน Google ชีต
วิธีสร้างแปลงที่เหลือใน Google ชีต