วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน google ชีต

ความแปรปรวนร่วม คือการวัดว่าการเปลี่ยนแปลงในตัวแปรหนึ่งสัมพันธ์กับการเปลี่ยนแปลงในตัวแปรตัวที่สองอย่างไร โดยเฉพาะอย่างยิ่ง มันคือการวัดระดับที่ตัวแปรสองตัวมีความสัมพันธ์กันเชิงเส้นตรง

สูตรคำนวณความแปรปรวนร่วมระหว่างตัวแปรสองตัว X และ Y คือ:

COV( X , Y ) = Σ(x- x )(y- y ) / n

เมทริกซ์ความแปรปรวนร่วม คือเมทริกซ์จตุรัสที่แสดงความแปรปรวนร่วมระหว่างตัวแปรต่างๆ มากมาย นี่อาจเป็นวิธีที่มีประโยชน์ในการทำความเข้าใจว่าตัวแปรต่างๆ เกี่ยวข้องกันอย่างไรในชุดข้อมูล

ตัวอย่างต่อไปนี้แสดงวิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน Google ชีตสำหรับชุดข้อมูลที่กำหนด

วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน Google ชีต

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ที่แสดงคะแนนสอบของนักเรียน 10 คนที่แตกต่างกันใน 3 วิชา ได้แก่ คณิตศาสตร์ วิทยาศาสตร์ และประวัติศาสตร์

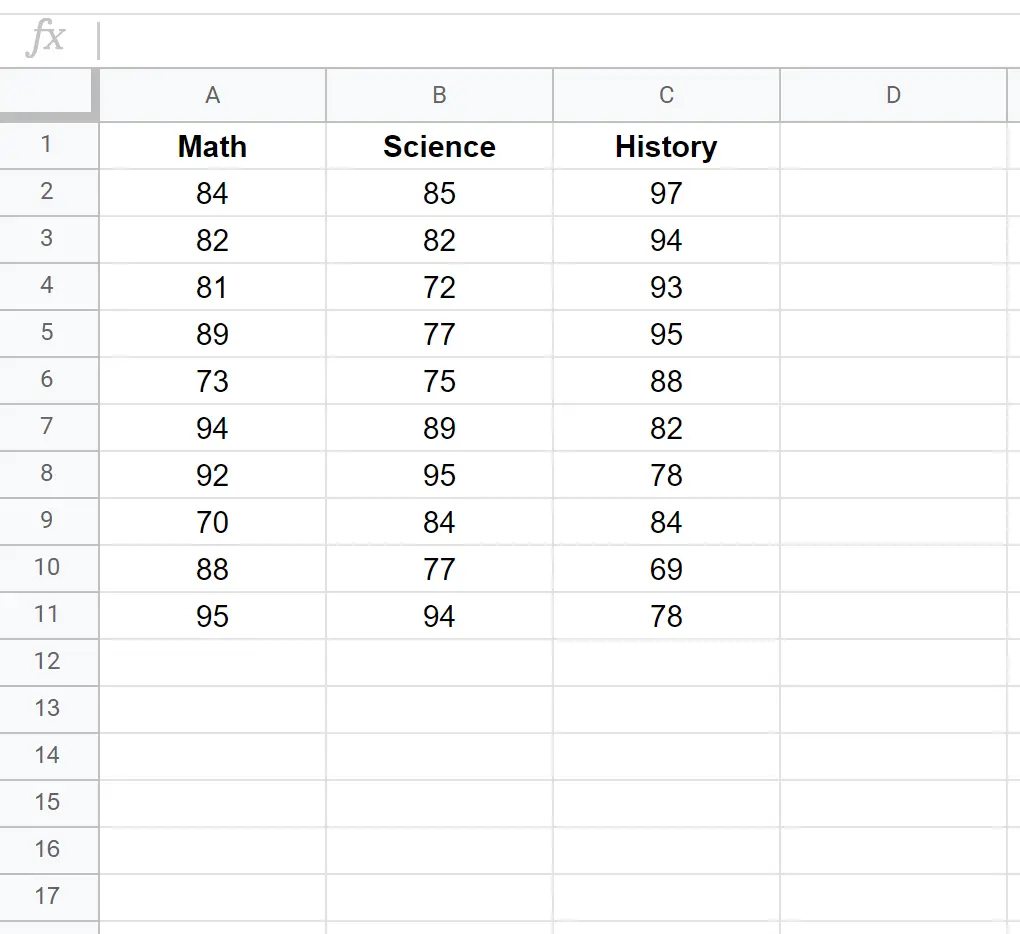
ในการสร้างเมทริกซ์ความแปรปรวนร่วมสำหรับชุดข้อมูลนี้ เราสามารถใช้ฟังก์ชัน COVAR() กับไวยากรณ์ต่อไปนี้:

COVAR(data_y, data_x)

เมทริกซ์ความแปรปรวนร่วมสำหรับชุดข้อมูลนี้จะแสดงในเซลล์ B15:D17 ในขณะที่สูตรที่ใช้สร้างเมทริกซ์ความแปรปรวนร่วมจะแสดงในเซลล์ B21:D23 ด้านล่าง:

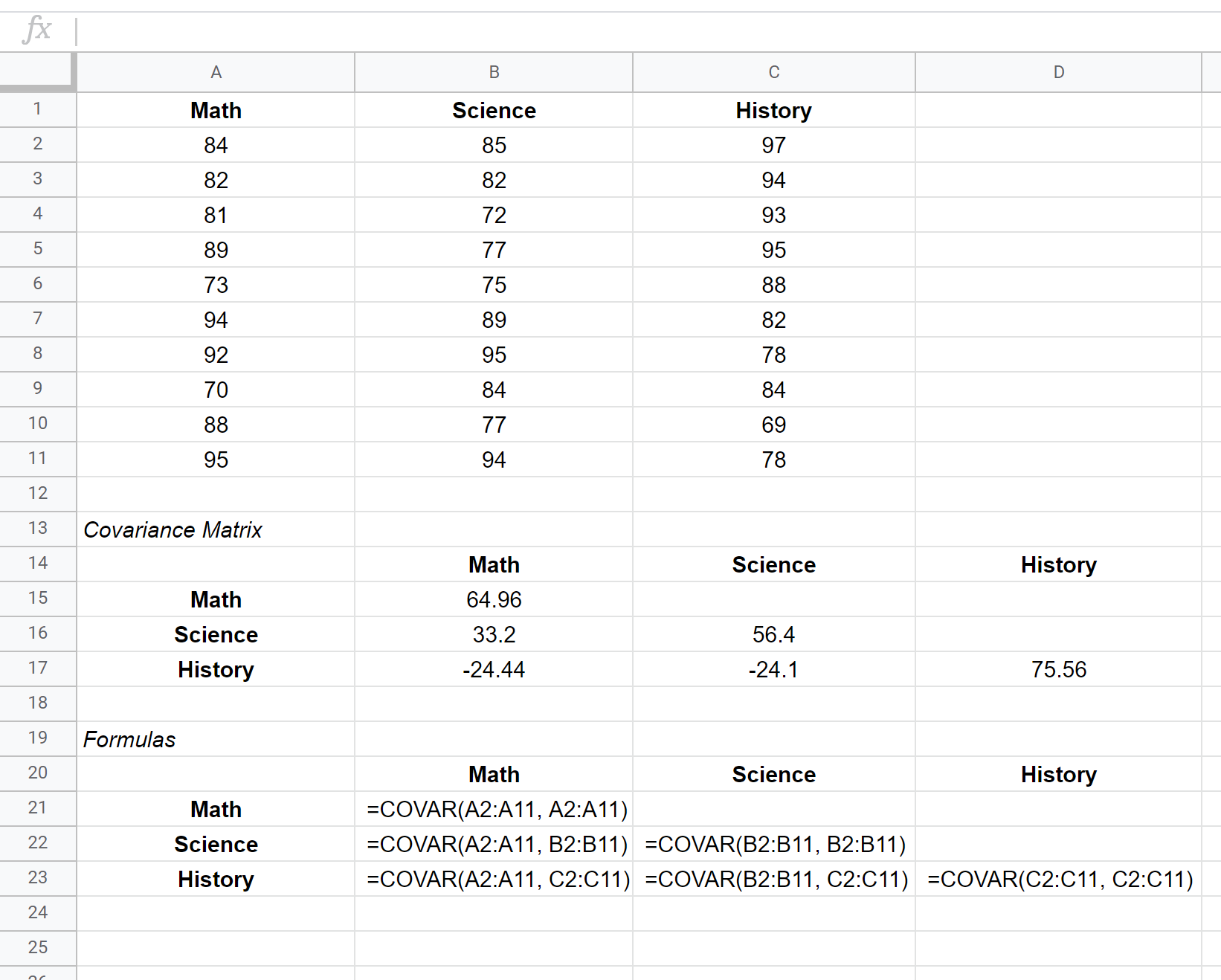
วิธีการตีความเมทริกซ์ความแปรปรวนร่วม

เมื่อเรามีเมทริกซ์ความแปรปรวนร่วมแล้ว การตีความค่าเมทริกซ์ก็เป็นเรื่องง่าย

ค่าตามเส้นทแยงมุมของเมทริกซ์เป็นเพียงความแปรปรวนของแต่ละเรื่อง ตัวอย่างเช่น:

• ความแปรปรวนของคะแนนคณิตศาสตร์คือ 64.96
• ความแปรปรวนของคะแนนวิทยาศาสตร์คือ 56.4
• ความแปรปรวนของคะแนนในอดีตคือ 75.56

ค่าอื่นๆ ของเมทริกซ์แสดงถึงความแปรปรวนร่วมระหว่างวิชาต่างๆ ตัวอย่างเช่น:

• ความแปรปรวนร่วมระหว่างคะแนนคณิตศาสตร์และวิทยาศาสตร์คือ 33.2
• ความแปรปรวนร่วมระหว่างคะแนนคณิตศาสตร์และประวัติศาสตร์คือ -24.44
• ความแปรปรวนร่วมระหว่างคะแนนวิทยาศาสตร์และประวัติศาสตร์คือ -24.1

จำนวนบวก สำหรับความแปรปรวนร่วมบ่งชี้ว่าตัวแปรสองตัวมีแนวโน้มเพิ่มขึ้นหรือลดลงตามกัน ตัวอย่างเช่น คณิตศาสตร์และวิทยาศาสตร์มีความแปรปรวนร่วมเชิงบวก (33.2) ซึ่งบ่งชี้ว่านักเรียนที่ได้คะแนนสูงในวิชาคณิตศาสตร์ก็มีแนวโน้มที่จะได้คะแนนสูงในวิชาวิทยาศาสตร์เช่นกัน ในทำนองเดียวกัน นักเรียนที่มีผลการเรียนไม่ดีในวิชาคณิตศาสตร์ก็มักจะมีผลการเรียนไม่ดีในวิชาวิทยาศาสตร์เช่นกัน

จำนวนลบ สำหรับความแปรปรวนร่วมบ่งชี้ว่าเมื่อตัวแปรตัวหนึ่งเพิ่มขึ้น ตัวแปรตัวที่สองมีแนวโน้มลดลง ตัวอย่างเช่น คณิตศาสตร์และประวัติศาสตร์มีความแปรปรวนร่วมเป็นลบ (-24.44) ซึ่งบ่งชี้ว่านักเรียนที่ได้คะแนนสูงในวิชาคณิตศาสตร์มักจะได้คะแนนต่ำในประวัติศาสตร์ ในทำนองเดียวกัน นักเรียนที่ได้คะแนนคณิตศาสตร์ต่ำมักจะได้คะแนนสูงในประวัติศาสตร์

แหล่งข้อมูลเพิ่มเติม

วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน Excel
วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน R
วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน Python
วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน SPSS