วิธีสร้างแปลงที่เหลือใน google ชีต

พล็อตส่วนที่เหลือ เป็นประเภทของพล็อตที่แสดงค่าที่ติดตั้งเทียบกับส่วนที่เหลือสำหรับแบบจำลองการถดถอย

พล็อตประเภทนี้มักใช้ในการประเมินว่าแบบจำลองการถดถอยเชิงเส้นมีความเหมาะสมสำหรับชุดข้อมูลที่กำหนดหรือไม่ และเพื่อตรวจสอบค่าคงเหลือสำหรับ ค่าเฮเทอโรสเคดาสติกซิตี

ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีสร้างพล็อตส่วนที่เหลือสำหรับโมเดลการถดถอยเชิงเส้นอย่างง่ายใน Google ชีต

ขั้นตอนที่ 1: ป้อนข้อมูล

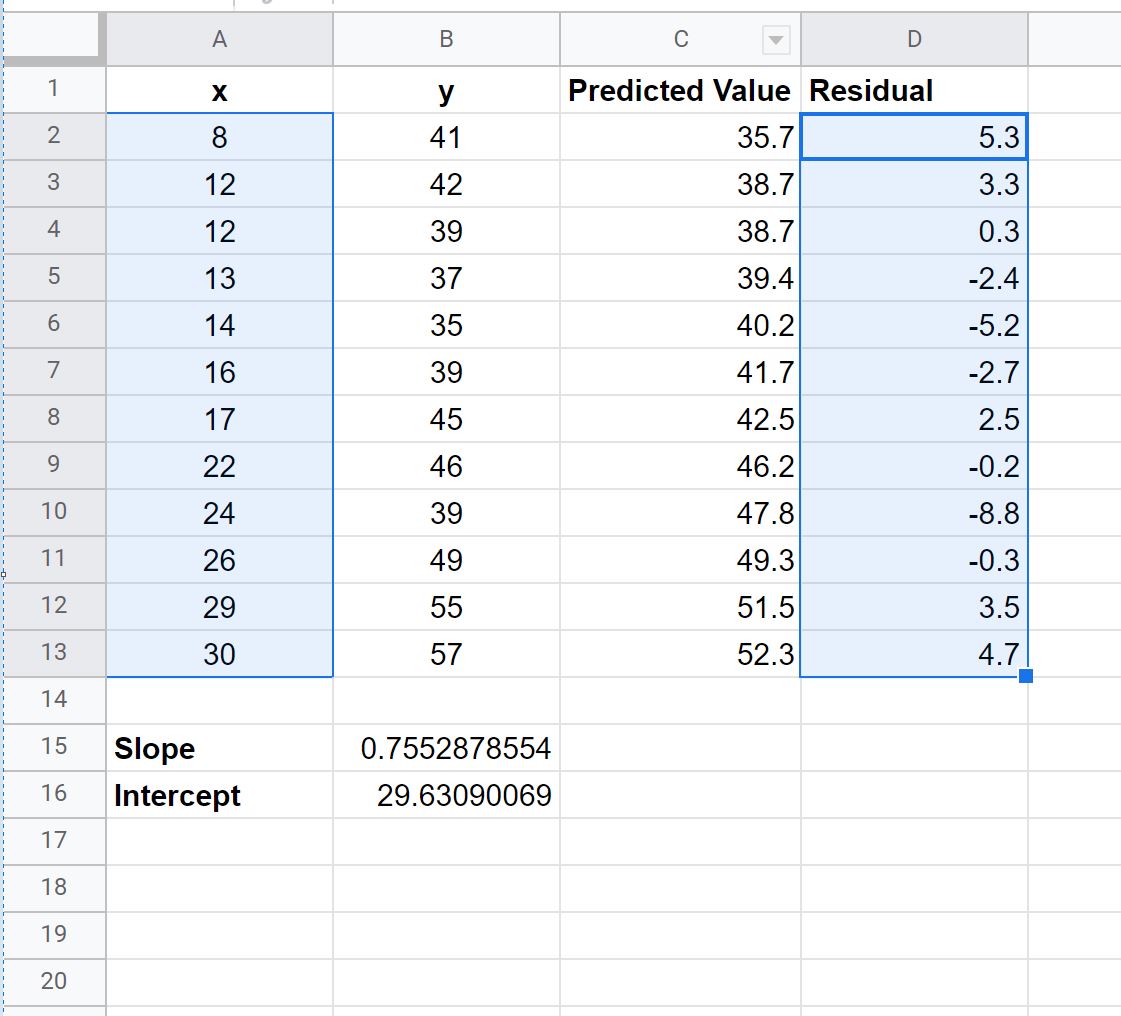
เริ่มต้นด้วยการป้อนค่าต่อไปนี้สำหรับชุดข้อมูล:

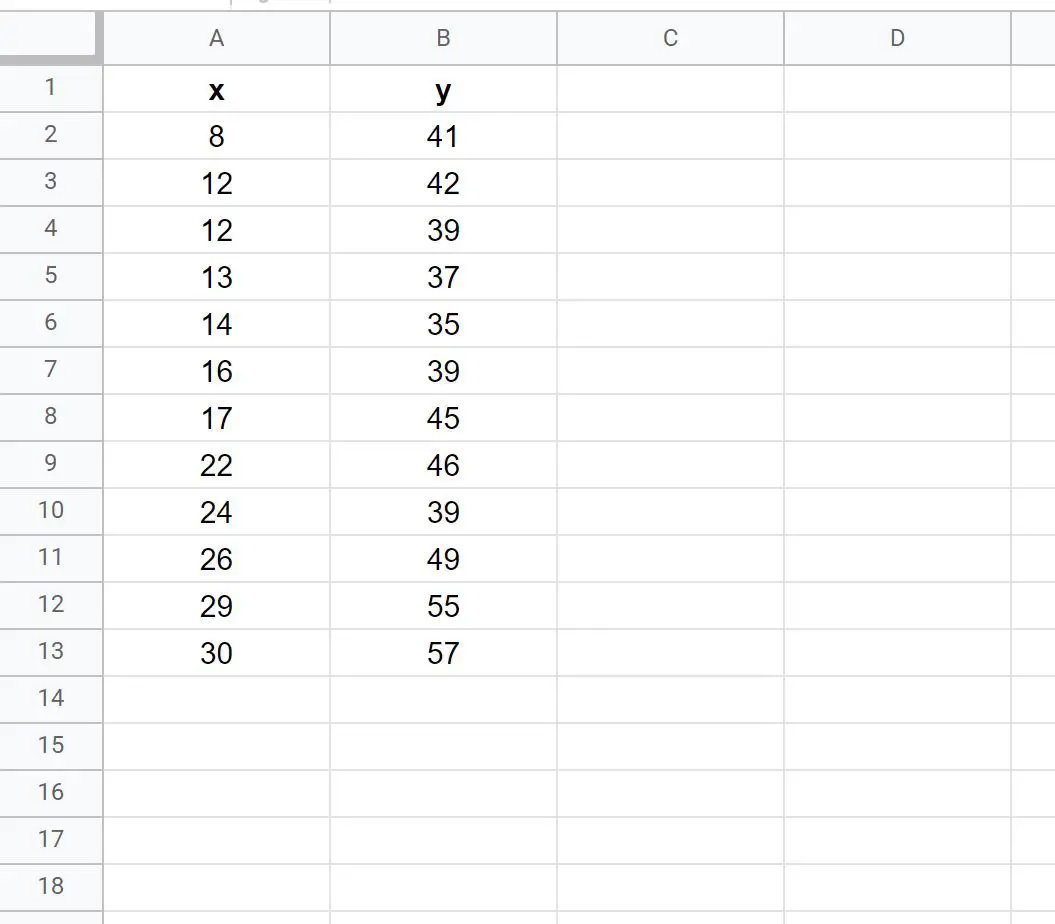
ขั้นตอนที่ 2: คำนวณสมการแบบจำลองการถดถอย

ต่อไป เราจะใช้ฟังก์ชัน SLOPE และ INTERCEPT เพื่อคำนวณสมการแบบจำลองการถดถอยเชิงเส้นอย่างง่ายสำหรับชุดข้อมูลนี้:

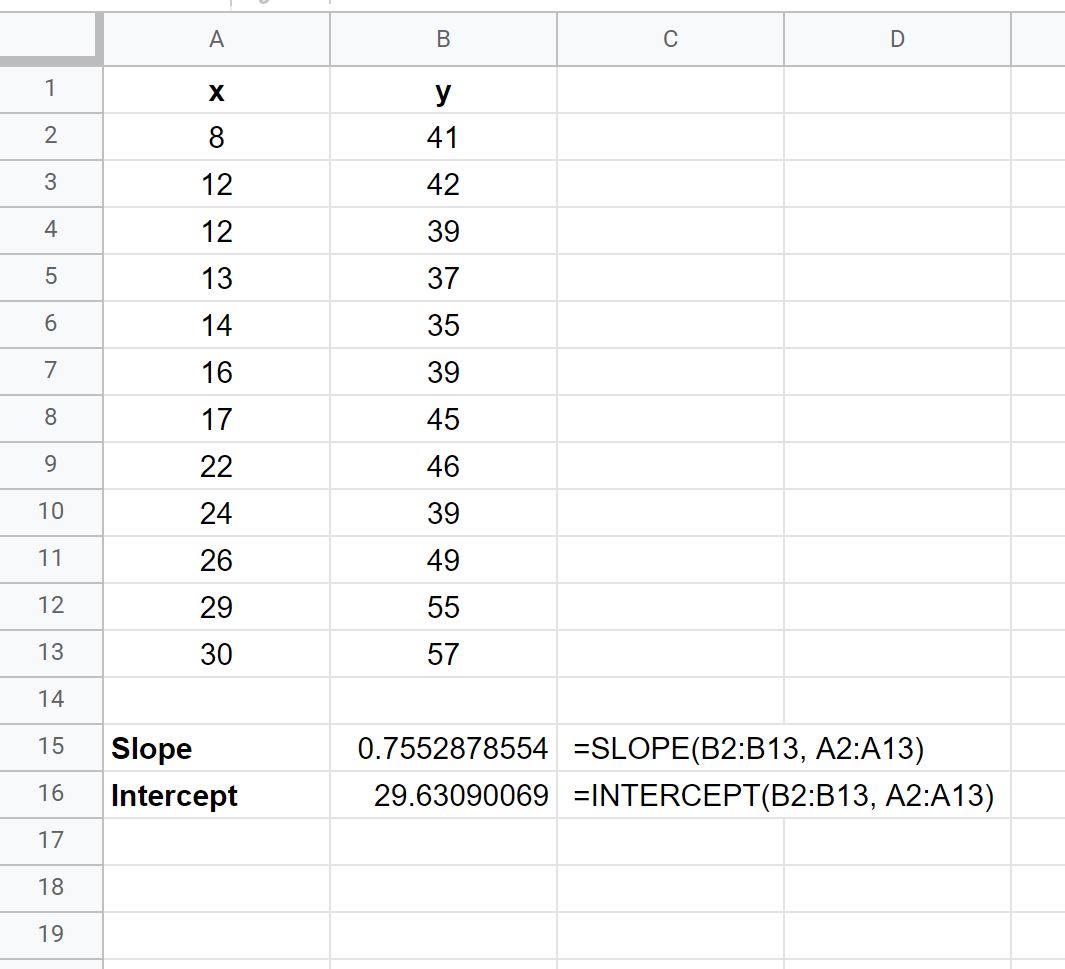
เมื่อใช้ค่าเหล่านี้ เราสามารถเขียนสมการการถดถอยเชิงเส้นอย่างง่ายต่อไปนี้:

y = 29.631 + 0.755x

ขั้นตอนที่ 3: คำนวณค่าที่ทำนายไว้

จากนั้นเราสามารถใช้สมการถดถอยเพื่อคำนวณค่าทำนายสำหรับการสังเกตแต่ละครั้ง

เราจะพิมพ์สูตรต่อไปนี้ในเซลล์ C2 :

 = $B$16 + $B$15 * A2

จากนั้นเราสามารถคัดลอกและวางสูตรนี้ลงในแต่ละเซลล์ที่เหลือในคอลัมน์ C :

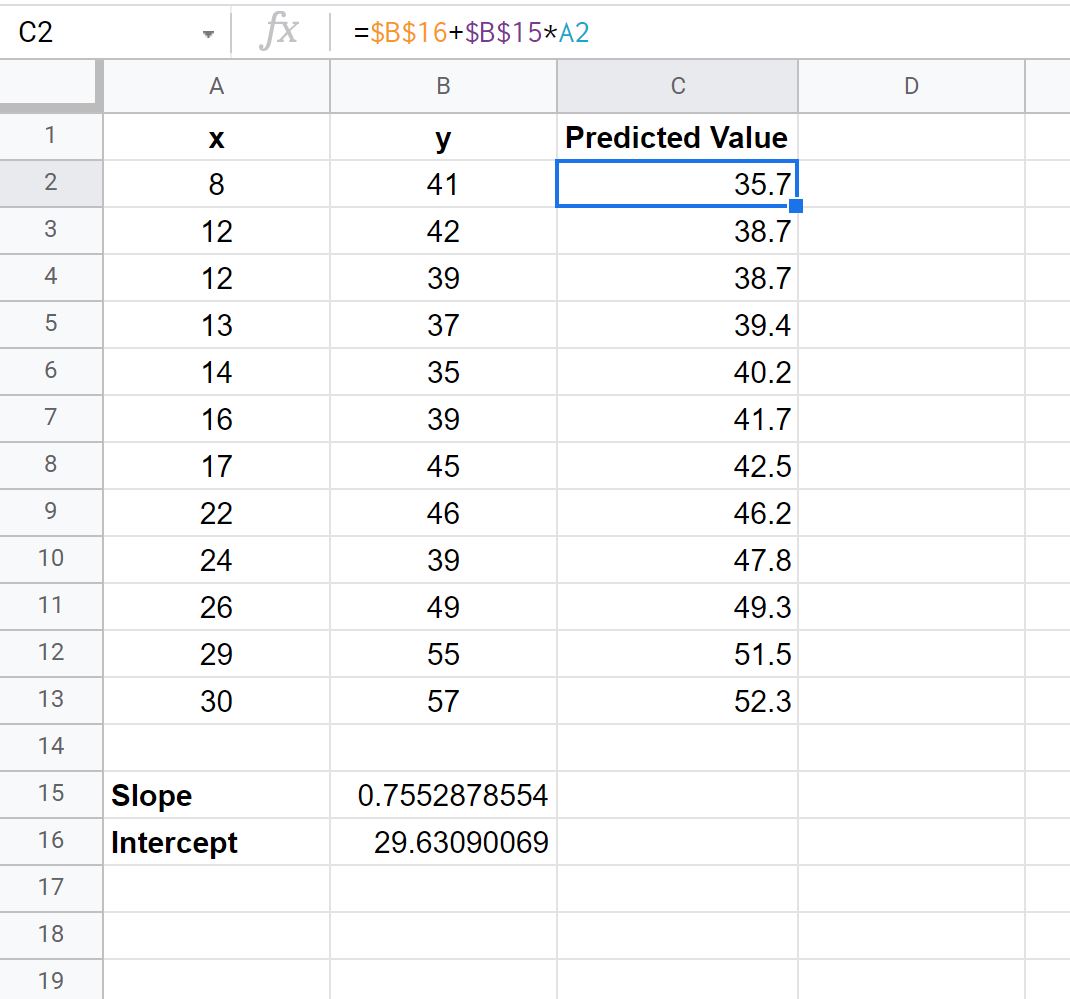
ขั้นตอนที่ 4: คำนวณปริมาณคงเหลือ

คงเหลือ คือความแตกต่างระหว่างค่าที่สังเกตได้กับค่าที่คาดการณ์ไว้ในแบบจำลองการถดถอย

มีการคำนวณดังนี้:

คงเหลือ = ค่าที่สังเกตได้ – ค่าที่คาดการณ์ไว้

ในการคำนวณค่าคงเหลือสำหรับการสังเกตแต่ละครั้งในชุดข้อมูลของเรา เราสามารถพิมพ์สูตรต่อไปนี้ในเซลล์ D2 :

 = B2 - C2

จากนั้นเราสามารถคัดลอกและวางสูตรนี้ลงในแต่ละเซลล์ที่เหลือในคอลัมน์ D :

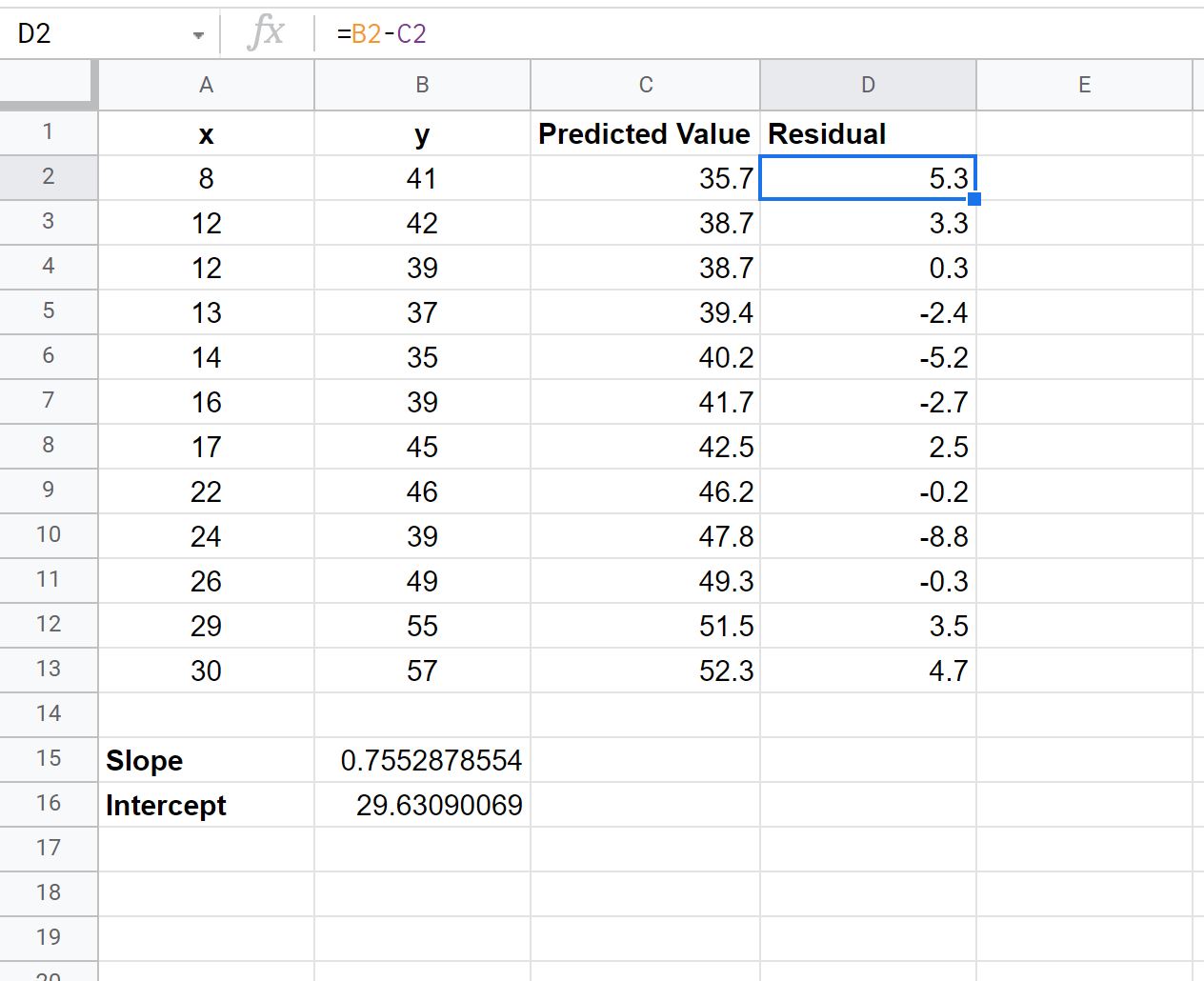
ขั้นตอนที่ 5: สร้างพล็อตที่เหลือ

ในการสร้างพล็อตที่เหลือเราสามารถเน้นค่าในช่วง A2:A13 จากนั้นกดปุ่ม “Ctrl” ค้างไว้และไฮไลต์ค่าในช่วง D2:D13 .

จากนั้นคลิกแท็บ แทรก จากนั้นคลิก แผนภูมิ ในเมนูแบบเลื่อนลง

ในแผง ตัวแก้ไขแผนภูมิ ที่ปรากฏทางด้านขวาของหน้าจอ ให้เลือก Scatter Plot เป็นประเภทแผนภูมิ:

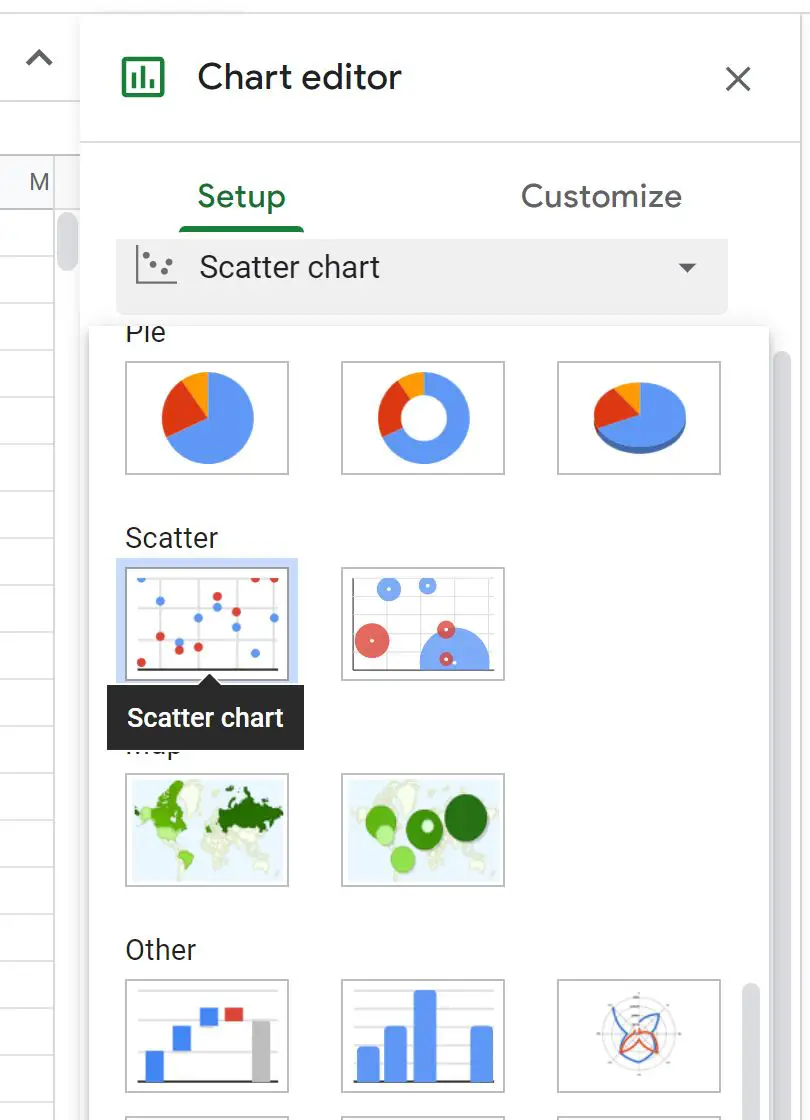
แปลงที่เหลือต่อไปนี้จะปรากฏขึ้นโดยอัตโนมัติ:

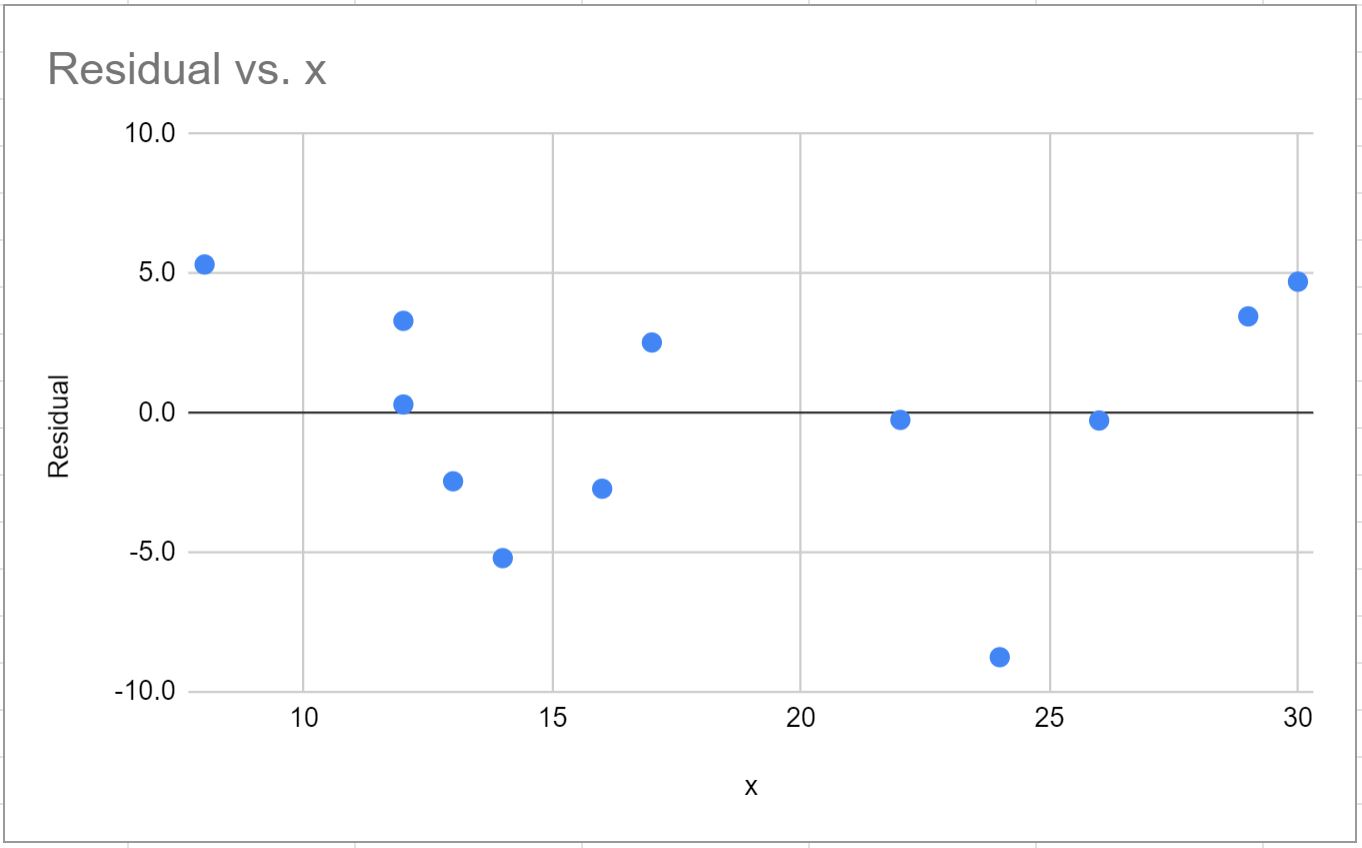
แกน x จะแสดงค่าของตัวแปรทำนายในแบบจำลองการถดถอยของเรา และแกน y จะแสดงค่าคงเหลือ

สมมติฐานหลัก ของการถดถอยเชิงเส้นคือส่วนที่เหลือมีความแปรปรวนคงที่ในแต่ละระดับของ x ดังนั้นเราจึงมักจะใช้แผนภาพของส่วนที่เหลือเพื่อพิจารณาว่าเป็นไปตามสมมติฐานนี้หรือไม่

ถ้าส่วนที่เหลือมีการกระจายเท่าๆ กันประมาณประมาณศูนย์ในกราฟโดยไม่มีแนวโน้มที่ชัดเจน โดยทั่วไปแล้วเราจะบอกว่าเป็นไปตามสมมติฐานของความแปรปรวนคงที่

ในแผนภาพส่วนที่เหลือของเราด้านบน เราจะเห็นว่าจุดต่างๆ ในแผนภาพดูเหมือนจะกระจัดกระจายแบบสุ่มรอบๆ ศูนย์โดยไม่มีรูปแบบที่ชัดเจน ดังนั้นเราจึงสรุปได้ว่าเป็นไปตามสมมติฐานความแปรปรวนคงที่สำหรับแบบจำลองการถดถอยเฉพาะนี้

แหล่งข้อมูลเพิ่มเติม

บทแนะนำต่อไปนี้จะอธิบายวิธีทำงานทั่วไปอื่นๆ ใน Google ชีต

วิธีดำเนินการถดถอยเชิงเส้นใน Google ชีต
วิธีดำเนินการถดถอยพหุนามใน Google ชีต