การจัดกลุ่ม k-means ใน r: ตัวอย่างทีละขั้นตอน

การจัดกลุ่มเป็นเทคนิคการเรียนรู้ของเครื่องที่พยายามค้นหา กลุ่ม ของ การสังเกต ภายในชุดข้อมูล

เป้าหมายคือการค้นหากระจุกที่การสังเกตภายในแต่ละกระจุกค่อนข้างคล้ายกัน ในขณะที่การสังเกตกระจุกที่ต่างกันจะค่อนข้างแตกต่างกัน

การจัดกลุ่มเป็นรูปแบบหนึ่งของ การเรียนรู้แบบไม่มีผู้ดูแล เนื่องจากเราเพียงพยายามค้นหาโครงสร้างภายในชุดข้อมูลแทนที่จะทำนายค่าของ ตัวแปรตอบสนอง

การจัดกลุ่มมักใช้ในการตลาดเมื่อธุรกิจสามารถเข้าถึงข้อมูลเช่น:

• รายได้ของครัวเรือน
• ขนาดครัวเรือน
• อาชีพหัวหน้าครัวเรือน
• ระยะทางไปยังเขตเมืองที่ใกล้ที่สุด

เมื่อมีข้อมูลนี้ การจัดกลุ่มสามารถใช้เพื่อระบุครัวเรือนที่คล้ายกันและอาจมีแนวโน้มที่จะซื้อผลิตภัณฑ์บางอย่างหรือตอบสนองต่อโฆษณาบางประเภทได้ดีขึ้น

รูปแบบการจัดกลุ่มรูปแบบหนึ่งที่พบบ่อยที่สุดเรียกว่า การจัดกลุ่มแบบเคมีน

การจัดกลุ่ม K-Means คืออะไร?

การจัดกลุ่มแบบเคมีนเป็นเทคนิคที่เราวางแต่ละการสังเกตจากชุดข้อมูลลงในคลัสเตอร์ K กลุ่มใดกลุ่มหนึ่ง

เป้าหมายสุดท้ายคือการมีกระจุกดาว K ซึ่งการสังเกตภายในแต่ละกระจุกจะค่อนข้างคล้ายกัน ในขณะที่การสังเกตในกลุ่มต่าง ๆ จะค่อนข้างแตกต่างกัน

ในทางปฏิบัติ เราใช้ขั้นตอนต่อไปนี้เพื่อดำเนินการจัดกลุ่ม K-mean:

1. เลือกค่าสำหรับ K

• ขั้นแรก เราต้องตัดสินใจว่าเราต้องการระบุคลัสเตอร์จำนวนเท่าใดในข้อมูล บ่อยครั้งที่เราเพียงแค่ต้องทดสอบค่า K ที่แตกต่างกันหลายค่า และวิเคราะห์ผลลัพธ์เพื่อดูว่าจำนวนคลัสเตอร์ใดที่ดูเหมือนจะเหมาะสมที่สุดสำหรับปัญหาที่กำหนด

2. สุ่มกำหนดแต่ละการสังเกตให้กับคลัสเตอร์เริ่มต้น ตั้งแต่ 1 ถึง K

3. ทำตามขั้นตอนต่อไปนี้จนกว่าการกำหนดคลัสเตอร์จะหยุดการเปลี่ยนแปลง

• สำหรับแต่ละกระจุก K ให้คำนวณ จุดศูนย์ถ่วงของกระจุก นี่เป็นเพียงเวกเตอร์ของคุณลักษณะ p- mean สำหรับการสังเกตคลัสเตอร์ที่ k
• กำหนดการสังเกตแต่ละครั้งให้กับคลัสเตอร์ที่มีจุดศูนย์กลางใกล้เคียงที่สุด ในที่นี้ ระยะทาง ที่ใกล้เคียงที่สุด ถูกกำหนดโดยใช้ ระยะทางแบบยุคลิด

การจัดกลุ่ม K-Means ใน R

บทช่วยสอนต่อไปนี้ให้ตัวอย่างทีละขั้นตอนของวิธีดำเนินการจัดกลุ่มเคมีนใน R

ขั้นตอนที่ 1: โหลดแพ็คเกจที่จำเป็น

ขั้นแรก เราจะโหลดแพ็คเกจสองแพ็คเกจที่มีฟังก์ชันที่มีประโยชน์มากมายสำหรับการจัดกลุ่มเคมีนใน R

 library (factoextra)
library (cluster)

ขั้นตอนที่ 2: โหลดและเตรียมข้อมูล

สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูล USArrests ที่สร้างไว้ใน R ซึ่งมีจำนวนการจับกุมต่อผู้คน 100,000 คนในแต่ละรัฐของสหรัฐอเมริกาในปี 1973 ในข้อหา ฆาตกรรม การทำร้ายร่างกาย และ การข่มขืน รวมถึงเปอร์เซ็นต์ของประชากรแต่ละรัฐที่อาศัยอยู่ในเมือง พื้นที่ , เออร์เบินป็อป .

รหัสต่อไปนี้แสดงวิธีการทำสิ่งต่อไปนี้:

• โหลดชุดข้อมูล USarrests
• ลบแถวทั้งหมดที่มีค่าหายไป
• ปรับขนาดตัวแปรแต่ละตัวในชุดข้อมูลให้มีค่าเฉลี่ยเป็น 0 และค่าเบี่ยงเบนมาตรฐานเป็น 1

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

ขั้นตอนที่ 3: ค้นหาจำนวนคลัสเตอร์ที่เหมาะสมที่สุด

ในการดำเนินการจัดกลุ่มเคมีนใน R เราสามารถใช้ฟังก์ชัน kmeans() ในตัว ซึ่งใช้ไวยากรณ์ต่อไปนี้:

kmeans (ข้อมูล, ศูนย์, nstart)

ทอง:

• data: ชื่อของชุดข้อมูล
• ศูนย์กลาง: จำนวนคลัสเตอร์ แทนด้วย k
• nstart: จำนวนการกำหนดค่าเริ่มต้น เนื่องจากเป็นไปได้ที่คลัสเตอร์เริ่มต้นที่แตกต่างกันจะนำไปสู่ผลลัพธ์ที่แตกต่างกัน จึงแนะนำให้ใช้การกำหนดค่าเริ่มต้นที่แตกต่างกันหลายรายการ อัลกอริธึมเคมีนจะค้นหาการกำหนดค่าเริ่มต้นที่นำไปสู่ความแปรผันที่น้อยที่สุดภายในคลัสเตอร์

เนื่องจากเราไม่ทราบล่วงหน้าว่ามีคลัสเตอร์กี่คลัสเตอร์ที่เหมาะสมที่สุด เราจะสร้างกราฟที่แตกต่างกันสองกราฟเพื่อช่วยเราตัดสินใจ:

1. จำนวนคลัสเตอร์ที่สัมพันธ์กับผลรวมของกำลังสอง

ขั้นแรก เราจะใช้ฟังก์ชัน fviz_nbclust() เพื่อสร้างพล็อตของจำนวนคลัสเตอร์เทียบกับผลรวมในผลรวมของกำลังสอง:

 fviz_nbclust(df, kmeans, method = “ wss ”) 

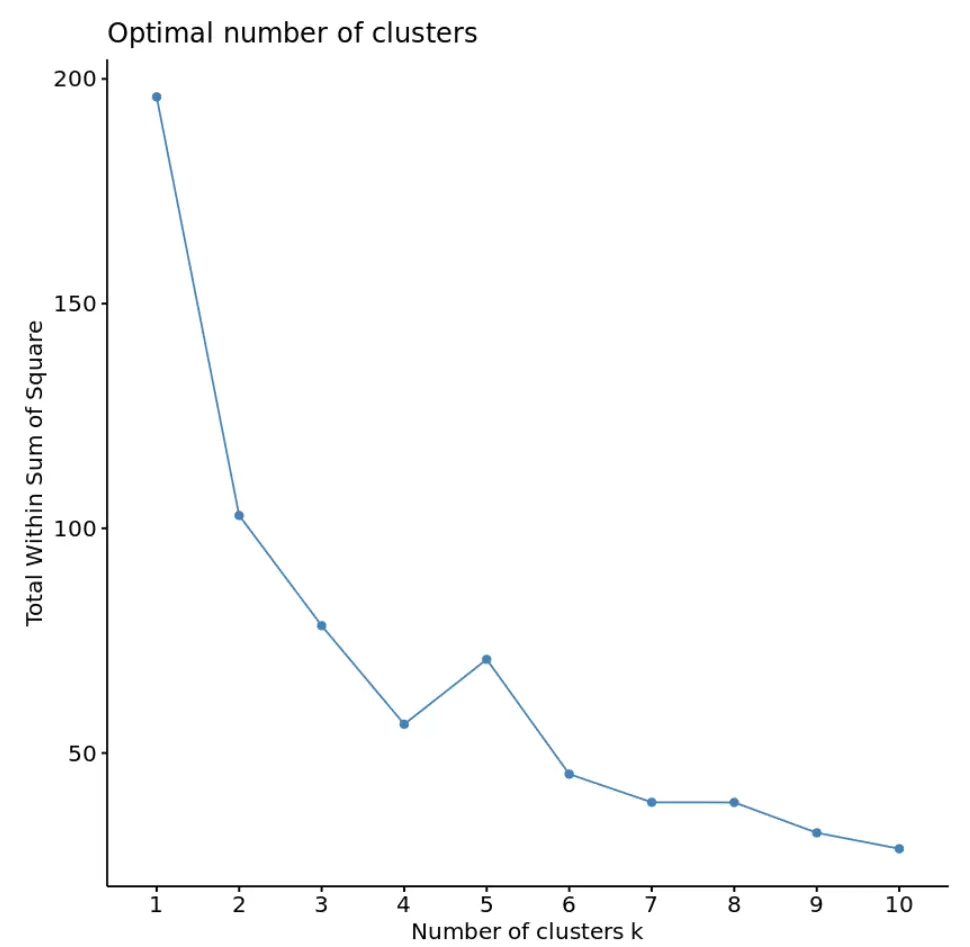
โดยทั่วไป เมื่อเราสร้างพล็อตประเภทนี้ เราจะมองหา “หัวเข่า” ซึ่งผลรวมของกำลังสองเริ่ม “โค้งงอ” หรือคลี่คลายลง โดยทั่วไปนี่คือจำนวนคลัสเตอร์ที่เหมาะสมที่สุด

สำหรับกราฟนี้ปรากฏว่ามีการงอหรือ “โค้งงอ” เล็กน้อยที่ k = 4 กระจุก

2. จำนวนคลัสเตอร์เทียบกับสถิติช่องว่าง

อีกวิธีหนึ่งในการกำหนดจำนวนคลัสเตอร์ที่เหมาะสมที่สุดคือการใช้ตัวชี้วัดที่เรียกว่า สถิติส่วนเบี่ยงเบน ซึ่งจะเปรียบเทียบความแปรผันภายในคลัสเตอร์ทั้งหมดสำหรับค่า k ที่แตกต่างกันกับค่าที่คาดหวังสำหรับการแจกแจงโดยไม่มีการจัดกลุ่ม

เราสามารถคำนวณสถิติช่องว่างสำหรับคลัสเตอร์แต่ละจำนวนได้โดยใช้ฟังก์ชัน clusGap() จากแพ็ก เกจคลัสเตอร์ ตลอดจนพล็อตคลัสเตอร์เทียบกับสถิติช่องว่างโดยใช้ฟังก์ชัน fviz_gap_stat()

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = kmeans,
                    nstart = 25,
                    K.max = 10,
                    B = 50)

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

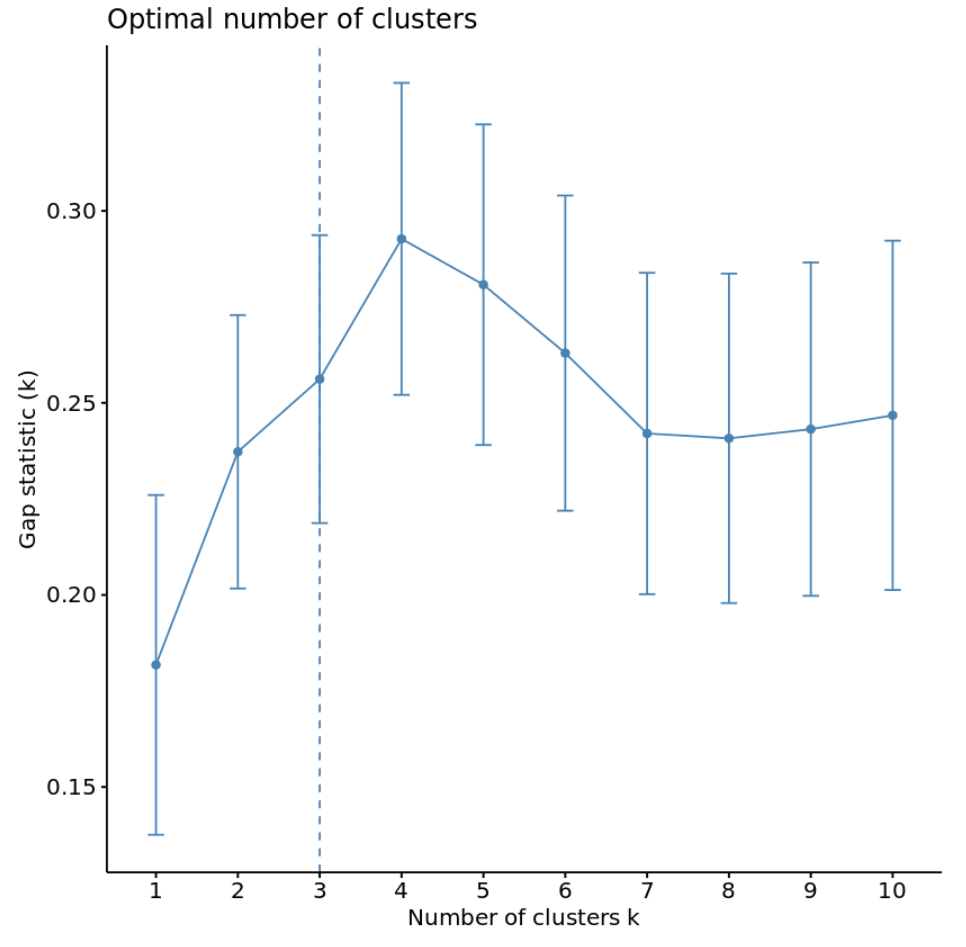
จากกราฟเราจะเห็นว่าสถิติช่องว่างสูงสุดที่ k = 4 กลุ่ม ซึ่งสอดคล้องกับวิธีข้อศอกที่เราใช้ก่อนหน้านี้

ขั้นตอนที่ 4: ดำเนินการจัดกลุ่ม K-Means ด้วย Optimal K

สุดท้ายนี้ เราสามารถดำเนินการจัดกลุ่มแบบเคมีนบนชุดข้อมูลโดยใช้ค่าที่เหมาะสมที่สุดสำหรับ k ของ 4:

 #make this example reproducible
set.seed(1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

จากผลลัพธ์เราจะเห็นได้ว่า:

• 16 รัฐถูกกำหนดให้กับคลัสเตอร์แรก
• 13 สถานะได้รับการกำหนดให้กับคลัสเตอร์ที่สอง
• 13 รัฐถูกกำหนดให้กับคลัสเตอร์ที่สาม
• 8 สถานะถูกกำหนดให้กับคลัสเตอร์ที่สี่

เราสามารถมองเห็นคลัสเตอร์บน Scatterplot ที่แสดงองค์ประกอบหลักสององค์ประกอบแรกบนแกนโดยใช้ฟังก์ชัน fivz_cluster() :

 #plot results of final k-means model
fviz_cluster(km, data = df)

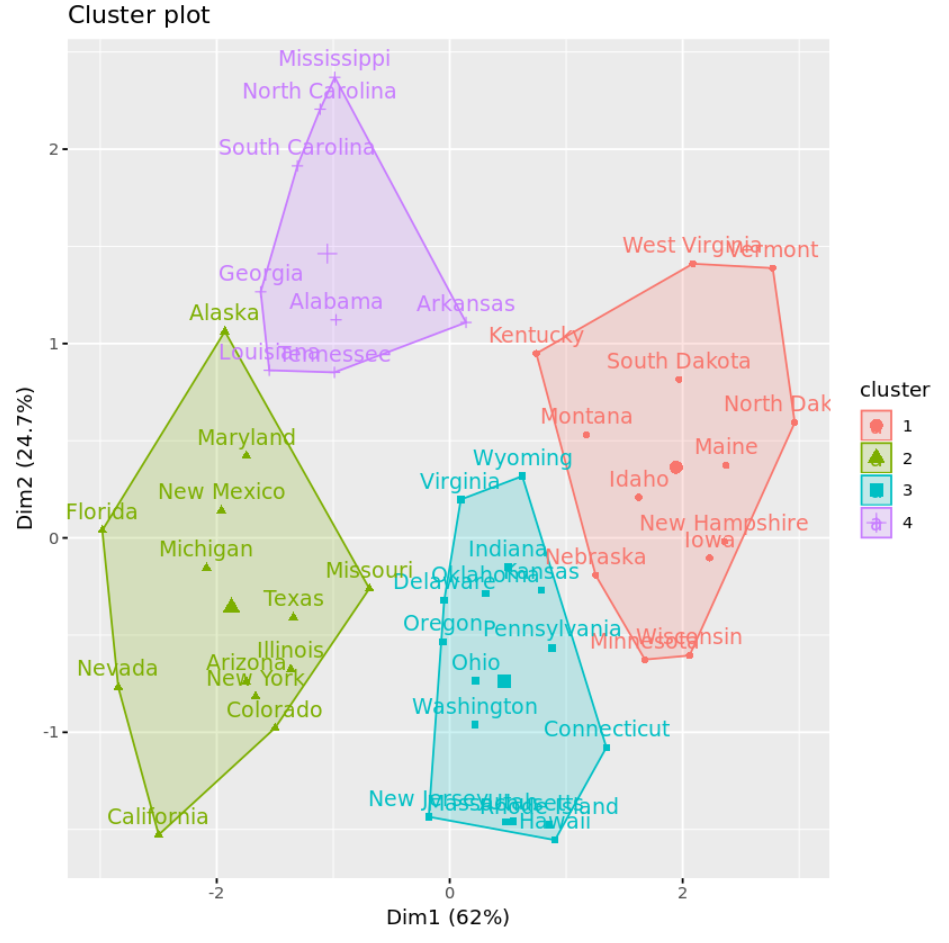
นอกจากนี้เรายังสามารถใช้ฟังก์ชัน Aggregate() เพื่อค้นหาค่าเฉลี่ยของตัวแปรในแต่ละคลัสเตอร์:

 #find means of each cluster
aggregate(USArrests, by= list (cluster=km$cluster), mean)

cluster Murder Assault UrbanPop Rape
				
1 3.60000 78.53846 52.07692 12.17692
2 10.81538 257.38462 76.00000 33.19231
3 5.65625 138.87500 73.87500 18.78125
4 13.93750 243.62500 53.75000 21.41250

เราตีความผลลัพธ์นี้ดังนี้:

• จำนวนการฆาตกรรมโดยเฉลี่ยต่อพลเมือง 100,000 คนในกลุ่มรัฐ 1 คือ 3.6
• จำนวนการโจมตีโดยเฉลี่ยต่อพลเมือง 100,000 คนในกลุ่มรัฐ 1 คือ 78.5
• เปอร์เซ็นต์เฉลี่ยของผู้อยู่อาศัยที่อาศัยอยู่ในเขตเมืองในกลุ่มรัฐ 1 คือ 52.1%
• จำนวนการข่มขืนโดยเฉลี่ยต่อพลเมือง 100,000 คนในรัฐกลุ่ม 1 คือ 12.2

และอื่นๆ

นอกจากนี้เรายังสามารถเพิ่มการกำหนดคลัสเตอร์ของแต่ละสถานะให้กับชุดข้อมูลดั้งเดิมได้:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

ข้อดีและข้อเสียของการจัดกลุ่ม K-Means

การจัดกลุ่ม K-means มีข้อดีดังต่อไปนี้:

• มันเป็นอัลกอริธึมที่รวดเร็ว
• สามารถจัดการชุดข้อมูลขนาดใหญ่ได้ดี

อย่างไรก็ตาม ก็มีข้อเสียที่อาจเกิดขึ้นได้ดังต่อไปนี้:

• สิ่งนี้กำหนดให้เราต้องระบุจำนวนคลัสเตอร์ก่อนที่จะรันอัลกอริทึม
• มันไวต่อค่าผิดปกติ

ทางเลือกสองทางสำหรับการจัดกลุ่มแบบเคมีนคือ การจัดกลุ่มแบบเคมีน และการจัดกลุ่มแบบลำดับชั้น

คุณสามารถค้นหาโค้ด R แบบเต็มที่ใช้ในตัวอย่างนี้ ได้ ที่นี่