Multicollinearity ที่สมบูรณ์แบบคืออะไร? (คำจำกัดความและตัวอย่าง)

ในสถิติ ความเป็น หลายคอลลิเนียริตี เกิดขึ้นเมื่อตัวแปรทำนายตั้งแต่สองตัวขึ้นไปมีความสัมพันธ์กันอย่างมาก โดยไม่ได้ให้ข้อมูลเฉพาะหรือเป็นอิสระในแบบจำลองการถดถอย

หากระดับความสัมพันธ์ระหว่างตัวแปรสูงเพียงพอ อาจทำให้เกิดปัญหาเมื่อปรับให้เหมาะสมและตีความแบบจำลองการถดถอย

กรณีที่รุนแรงที่สุดของ multicollinearity เรียกว่า multicollinearity ที่สมบูรณ์แบบ สิ่งนี้เกิดขึ้นเมื่อตัวแปรทำนายตั้งแต่สองตัวขึ้นไปมีความสัมพันธ์เชิงเส้นตรงต่อกัน

ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลต่อไปนี้:

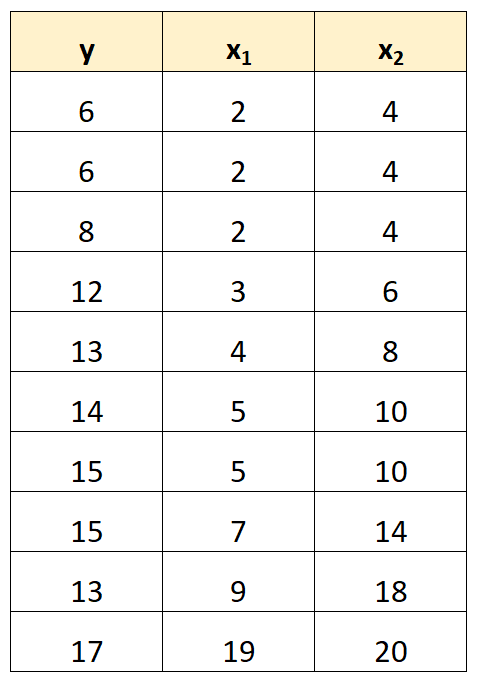
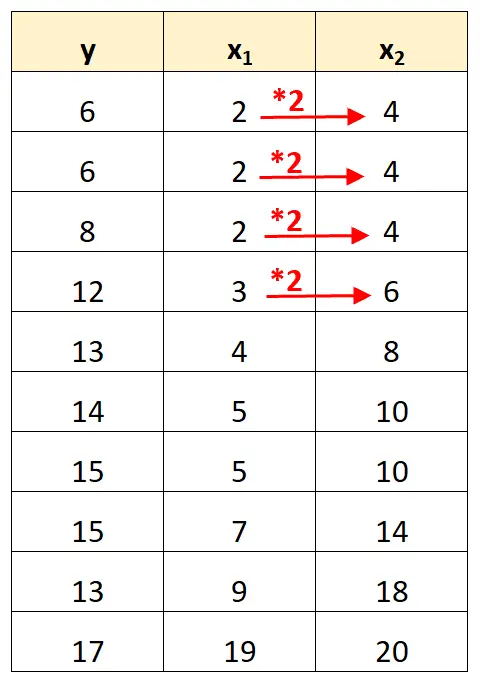
โปรดทราบว่าค่าของตัวแปรทำนาย x ₂ เป็นเพียงค่าของ x ₁ คูณด้วย 2

นี่คือตัวอย่างของ multicollinearity ที่สมบูรณ์แบบ

ปัญหาของ multicollinearity ที่สมบูรณ์แบบ

เมื่อชุดข้อมูลมีพหุคอลลิเนียร์ที่สมบูรณ์แบบ ชุดกำลังสองน้อยที่สุดธรรมดาจะไม่สามารถประมาณค่าสัมประสิทธิ์การถดถอยได้

อันที่จริง เป็นไปไม่ได้ที่จะประมาณผลส่วนเพิ่มของตัวแปรทำนาย (x ₁ ) ต่อตัวแปรตอบสนอง (y) ในขณะที่คงตัวแปรทำนายอื่น (x ₂ ) ไว้คงที่ เนื่องจาก x ₂ จะเคลื่อนที่เสมอเมื่อ x ₁ เคลื่อนที่

กล่าวโดยสรุป ความเป็นหลายเส้นตรงที่สมบูรณ์แบบทำให้ไม่สามารถประมาณค่าสัมประสิทธิ์แต่ละค่าในแบบจำลองการถดถอยได้

วิธีจัดการกับ multicollinearity ที่สมบูรณ์แบบ

วิธีที่ง่ายที่สุดในการจัดการกับความเป็นหลายเส้นตรงที่สมบูรณ์แบบคือการลบตัวแปรตัวใดตัวหนึ่งที่มีความสัมพันธ์เชิงเส้นตรงกับตัวแปรตัวอื่นออก

ตัวอย่างเช่น ในชุดข้อมูลก่อนหน้านี้ เราสามารถลบ x ₂ ออกจากการเป็นตัวแปรทำนายได้

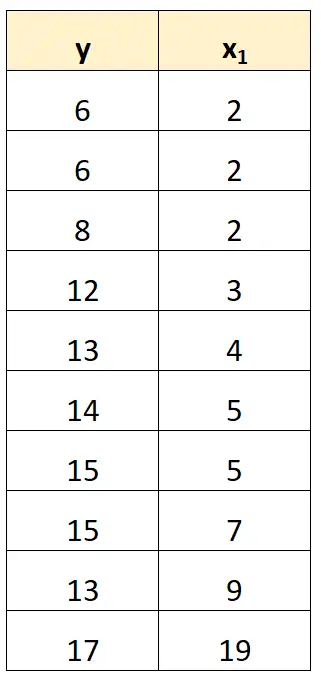
จากนั้นเราจะปรับโมเดลการถดถอยโดยใช้ x ₁ เป็นตัวแปรทำนายและ y เป็นตัวแปรตอบสนอง

ตัวอย่างของ multicollinearity ที่สมบูรณ์แบบ

ตัวอย่างต่อไปนี้แสดงสถานการณ์สมมติสามประการที่พบบ่อยที่สุดของ multicollinearity ที่สมบูรณ์แบบในทางปฏิบัติ

1. ตัวแปรทำนายเป็นผลคูณของตัวแปรอื่น

สมมติว่าเราต้องการใช้ “ความสูงเป็นเซนติเมตร” และ “ความสูงเป็นเมตร” เพื่อทำนายน้ำหนักของโลมาบางสายพันธุ์

นี่คือลักษณะของชุดข้อมูลของเรา:

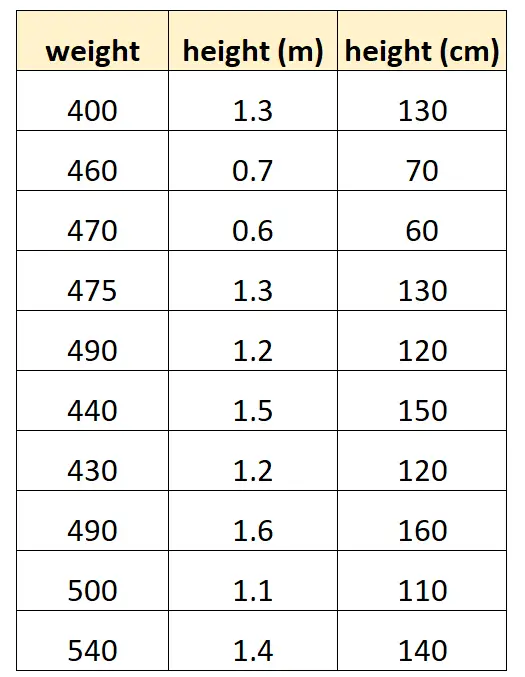
โปรดทราบว่าค่าของ “ความสูงเป็นเซนติเมตร” ก็เท่ากับ “ความสูงเป็นเมตร” คูณด้วย 100 นี่เป็นกรณีของความเป็นเส้นตรงที่สมบูรณ์แบบ

หากเราพยายามปรับโมเดลการถดถอยเชิงเส้นหลายตัวใน R โดยใช้ชุดข้อมูลนี้ เราจะไม่สามารถประมาณค่าสัมประสิทธิ์สำหรับตัวแปรทำนาย “เมตร” ได้:

 #define data
df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-70,501 -25,501 5,183 19,499 68,590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 458,676 53,403 8,589 2.61e-05 ***
m 9.096 43.473 0.209 0.839    
cm NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395

2. ตัวแปรทำนายคือเวอร์ชันที่ถูกแปลงของตัวแปรอื่น

สมมติว่าเราต้องการใช้ “คะแนน” และ “คะแนนที่ปรับขนาด” เพื่อทำนายอันดับของผู้เล่นบาสเก็ตบอล

สมมติว่าตัวแปร “คะแนนมาตราส่วน” ถูกคำนวณเป็น:

จุดที่ปรับขนาด = (จุด – μ _จุด ) / σ _จุด

นี่คือลักษณะของชุดข้อมูลของเรา:

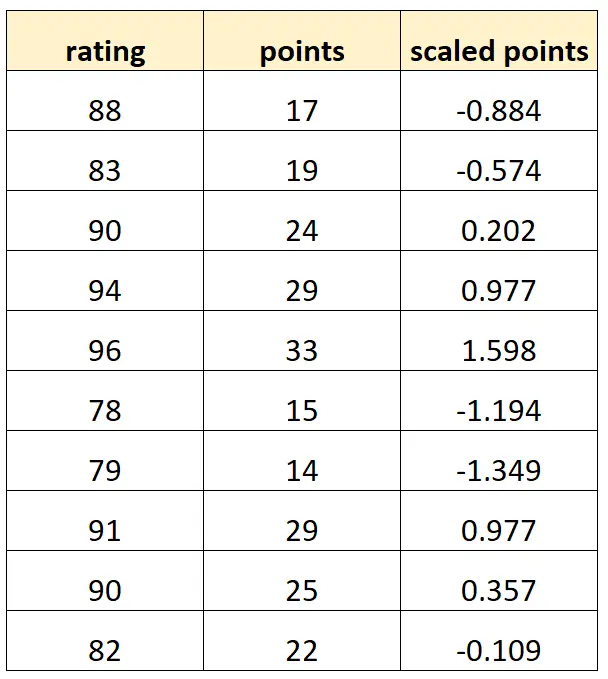
โปรดทราบว่าค่า “คะแนนที่ปรับขนาด” แต่ละค่าเป็นเพียง “คะแนน” ในเวอร์ชันมาตรฐาน นี่เป็นกรณีของ multicollinearity ที่สมบูรณ์แบบ

หากเราพยายามปรับโมเดลการถดถอยเชิงเส้นหลายตัวใน R โดยใช้ชุดข้อมูลนี้ เราจะไม่สามารถประมาณค่าสัมประสิทธิ์สำหรับตัวแปรทำนาย “จุดที่ปรับขนาด” ได้:

 #define data
df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4932 -1.3941 -0.2935 1.3055 5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 67.4218 3.5896 18.783 6.67e-08 ***
pts 0.8669 0.1527 5.678 0.000466 ***
scaled_pts NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663

3. กับดักตัวแปรจำลอง

อีกสถานการณ์หนึ่งที่อาจเกิด multicollinearity ที่สมบูรณ์แบบได้เรียกว่ากับ ดักตัวแปรจำลอง นี่คือเวลาที่เราต้องการนำตัวแปรเด็ดขาดในแบบจำลองการถดถอยแล้วแปลงเป็น “ตัวแปรจำลอง” ที่ใช้ค่า 0, 1, 2 เป็นต้น

ตัวอย่างเช่น สมมติว่าเราต้องการใช้ตัวแปรทำนาย “อายุ” และ “สถานภาพสมรส” เพื่อทำนายรายได้:

หากต้องการใช้ “สถานภาพสมรส” เป็นตัวแปรทำนาย เราต้องแปลงเป็นตัวแปรจำลองก่อน

ในการทำเช่นนี้เราสามารถปล่อยให้ “โสด” เป็นค่าฐานได้เนื่องจากสิ่งนี้เกิดขึ้นบ่อยที่สุดและกำหนดค่า 0 หรือ 1 ให้กับ “แต่งงานแล้ว” และ “หย่าร้าง” ดังนี้:

ข้อผิดพลาดคือการสร้างตัวแปรจำลองใหม่สามตัวดังนี้:

ในกรณีนี้ ตัวแปร “โสด” เป็นการผสมผสานเชิงเส้นที่สมบูรณ์แบบของตัวแปร “แต่งงานแล้ว” และ “หย่าร้าง” นี่คือตัวอย่างของความเป็นหลายเส้นตรงที่สมบูรณ์แบบ

หากเราพยายามปรับโมเดลการถดถอยเชิงเส้นหลายตัวใน R โดยใช้ชุดข้อมูลนี้ เราจะไม่สามารถประมาณค่าสัมประสิทธิ์สำหรับตัวแปรทำนายแต่ละตัวได้:

 #define data
df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-9.7075 -5.0338 0.0453 3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 16.7559 17.7811 0.942 0.37739   
age 1.4717 0.3544 4.152 0.00428 **
single -2.4797 9.4313 -0.263 0.80018   
married NA NA NA NA   
divorced -8.3974 12.7714 -0.658 0.53187   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865

แหล่งข้อมูลเพิ่มเติม

คู่มือเกี่ยวกับพหุคอลลิเนียร์ริตีและ VIF ในการถดถอย
วิธีการคำนวณ VIF ใน R
วิธีการคำนวณ VIF ใน Python
วิธีการคำนวณ VIF ใน Excel