วิธีการคำนวณความน่าจะเป็น normalcdf ใน excel

ฟังก์ชัน NormalCDF บนเครื่องคิดเลข TI-83 หรือ TI-84 สามารถใช้ค้นหาความน่าจะเป็นที่ ตัวแปรสุ่มแบบ กระจายแบบปกติรับค่าภายในช่วงที่กำหนด

บนเครื่องคิดเลข TI-83 หรือ TI-84 ฟังก์ชันนี้ใช้ไวยากรณ์ต่อไปนี้

Normalcdf (ล่าง, บน, μ, σ)

ทอง:

• ต่ำกว่า = ค่าที่ต่ำกว่าของช่วง
• upper = ค่าบนของช่วง
• μ = ค่าเฉลี่ยประชากร
• σ = ส่วนเบี่ยงเบนมาตรฐานประชากร

ตัวอย่างเช่น สมมติว่าตัวแปรสุ่ม ปกติมีการแจกแจง ด้วยค่าเฉลี่ย 50 และค่าเบี่ยงเบนมาตรฐาน 4 ความน่าจะเป็นที่ตัวแปรสุ่มจะมีค่าระหว่าง 48 ถึง 52 สามารถคำนวณได้ดังนี้

ปกติcdf(48, 52, 50, 4) = 0.3829

เราสามารถสร้างการตอบสนองนี้ซ้ำใน Excel โดยใช้ฟังก์ชัน NORM.DIST() ซึ่งใช้ไวยากรณ์ต่อไปนี้:

NORM.DIST(x, σ, μ, สะสม)

ทอง:

• x = ค่าข้อมูลแต่ละรายการ
• μ = ค่าเฉลี่ยประชากร
• σ = ส่วนเบี่ยงเบนมาตรฐานประชากร
• สะสม = FALSE คำนวณ PDF; TRUE คำนวณ CDF

ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้ในทางปฏิบัติ

ตัวอย่างที่ 1: ความน่าจะเป็นระหว่างสองค่า

สมมติว่าตัวแปรสุ่มปกติมีการแจกแจงด้วยค่าเฉลี่ย 50 และค่าเบี่ยงเบนมาตรฐาน 4 ความน่าจะเป็นที่ตัวแปรสุ่มจะมีค่า ระหว่าง 48 ถึง 52 สามารถคำนวณได้ดังนี้

 =NORM. DIST (52, 50, 4, TRUE ) - NORM. DIST (48, 50, 4, TRUE )

รูปภาพต่อไปนี้แสดงวิธีการคำนวณใน Excel:

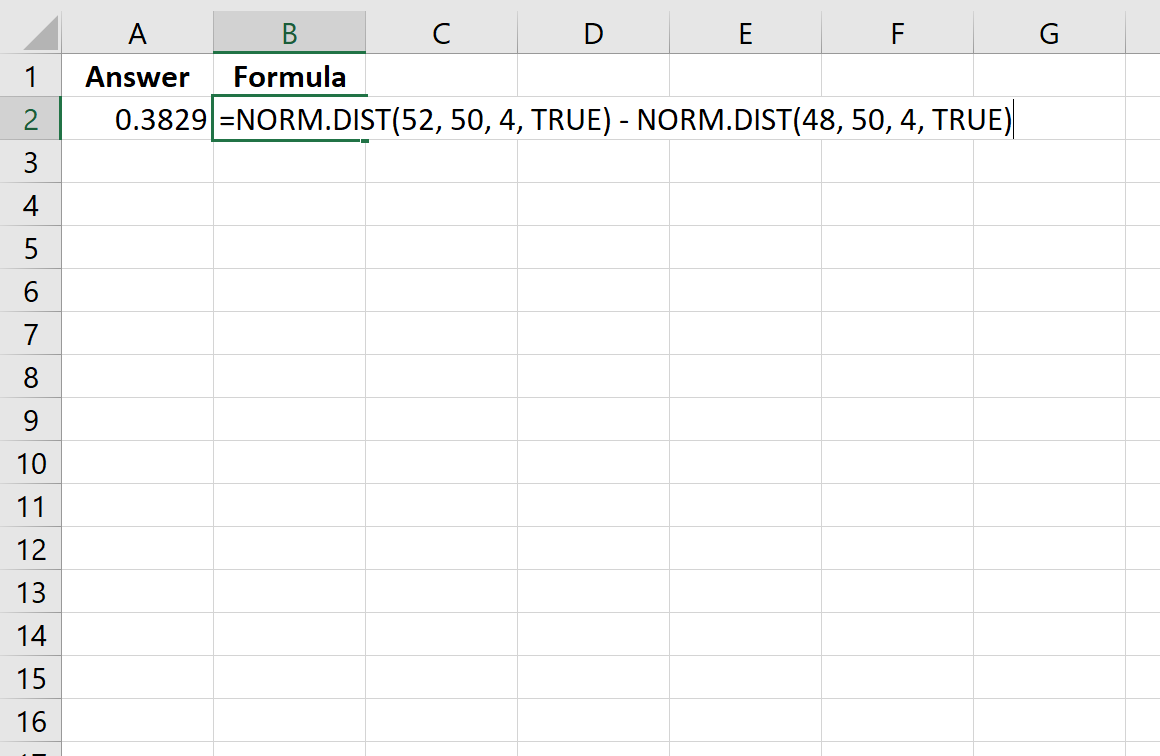
ความน่าจะเป็นกลายเป็น 0.3829

ตัวอย่างที่ 2: ความน่าจะเป็นน้อยกว่าหนึ่งค่า

สมมติว่าตัวแปรสุ่มมีการแจกแจงตามปกติโดยมีค่าเฉลี่ย 50 และค่าเบี่ยงเบนมาตรฐาน 4 ความน่าจะเป็นที่ตัวแปรสุ่มจะมีค่า น้อยกว่า 48 สามารถคำนวณได้ดังนี้

 =NORM. DIST (48, 50, 4, TRUE )

รูปภาพต่อไปนี้แสดงวิธีการคำนวณใน Excel:

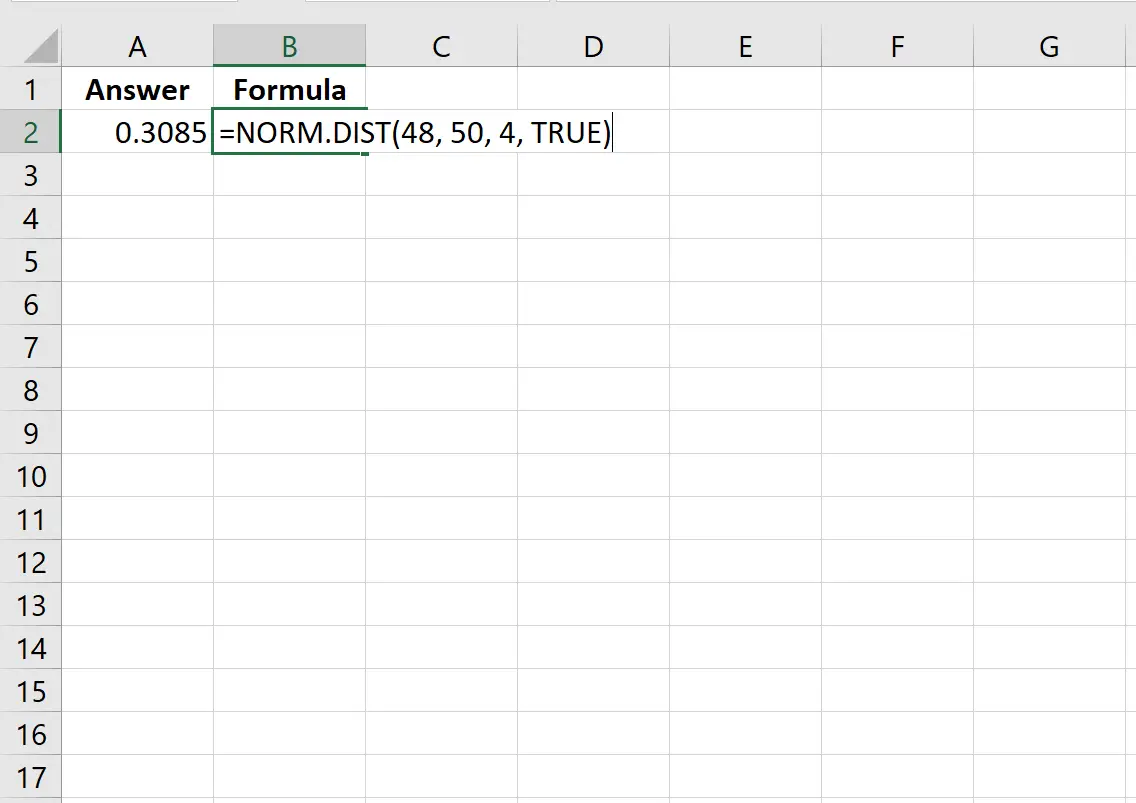
ความน่าจะเป็นกลายเป็น 0.3085

ตัวอย่างที่ 3: ความน่าจะเป็นที่มากกว่าค่า

สมมติว่าตัวแปรสุ่มมีการแจกแจงตามปกติโดยมีค่าเฉลี่ย 50 และค่าเบี่ยงเบนมาตรฐาน 4 ความน่าจะเป็นที่ตัวแปรสุ่มจะมีค่า มากกว่า 55 สามารถคำนวณได้ดังนี้

 =1 - NORM. DIST (55, 50, 4, TRUE )

รูปภาพต่อไปนี้แสดงวิธีการคำนวณใน Excel:

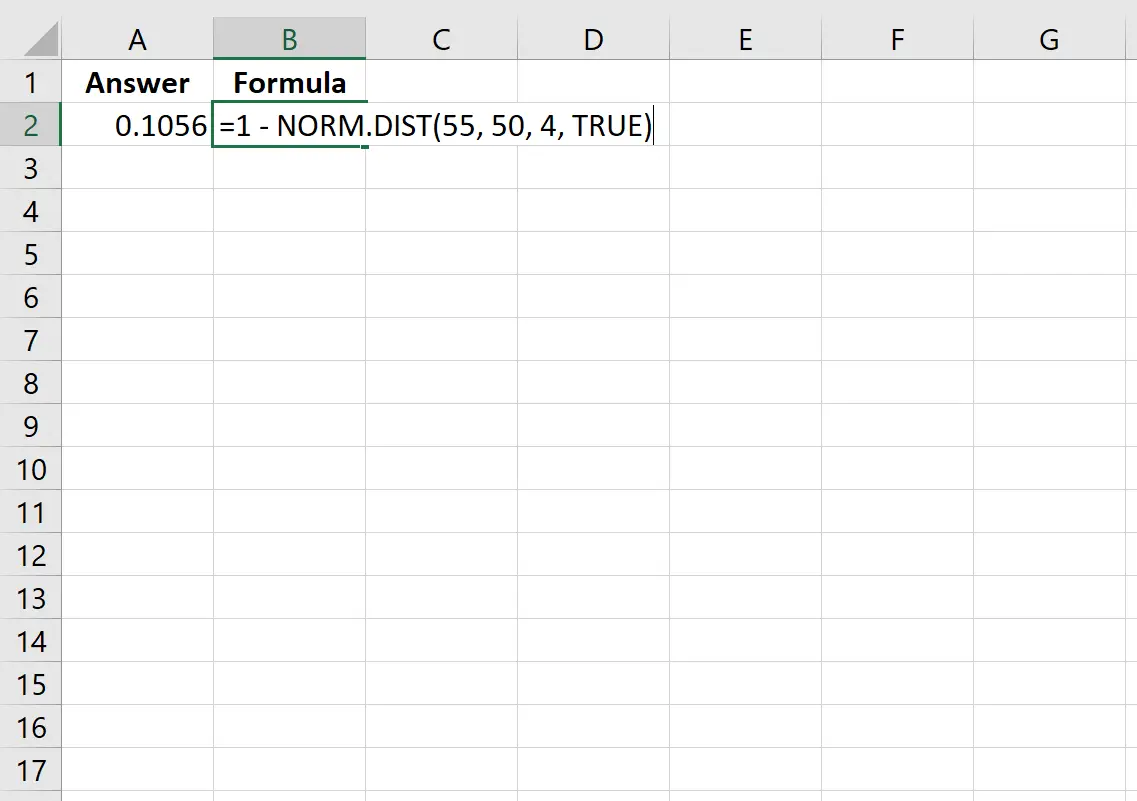
ความน่าจะเป็นกลายเป็น 0.1056

แหล่งข้อมูลเพิ่มเติม

คุณยังสามารถใช้ เครื่องคำนวณ CDF ปกติ นี้เพื่อค้นหาความน่าจะเป็นที่เกี่ยวข้องกับการแจกแจงแบบปกติได้โดยอัตโนมัติ