R กับ r-square: อะไรคือความแตกต่าง?

คำสองคำที่นักเรียนมักสับสนในสถิติคือ R และ R-squared ซึ่งมักเขียนเป็น ^R2

ในบริบทของ การถดถอยเชิงเส้นอย่างง่าย :

• ตอบ: ความสัมพันธ์ระหว่างตัวแปรทำนาย x และตัวแปรตอบสนอง y
• R ² : สัดส่วนของความแปรปรวนในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรทำนายในแบบจำลองการถดถอย

และในบริบทของ การถดถอยเชิงเส้นพหุคูณ :

• ตอบ: ความสัมพันธ์ระหว่างค่าที่สังเกตได้ของตัวแปรตอบสนองกับค่าที่ทำนายไว้ของตัวแปรตอบสนองที่สร้างโดยแบบจำลอง
• R ² : สัดส่วนของความแปรปรวนของตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรทำนายของแบบจำลองการถดถอย

โปรดทราบว่าค่าของ R ² อยู่ระหว่าง 0 ถึง 1 ยิ่งค่าเข้าใกล้ 1 มากเท่าใด ความสัมพันธ์ระหว่างตัวแปรทำนายและตัวแปรตอบสนองก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น

ตัวอย่างต่อไปนี้แสดงวิธีตีความค่า R และ R-squared ในการถดถอยเชิงเส้นอย่างง่ายและแบบจำลองการถดถอยเชิงเส้นหลายตัว

ตัวอย่างที่ 1: การถดถอยเชิงเส้นอย่างง่าย

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งแสดงชั่วโมงเรียนและคะแนนสอบที่นักเรียน 12 คนได้รับในหลักสูตรคณิตศาสตร์บางหลักสูตร:

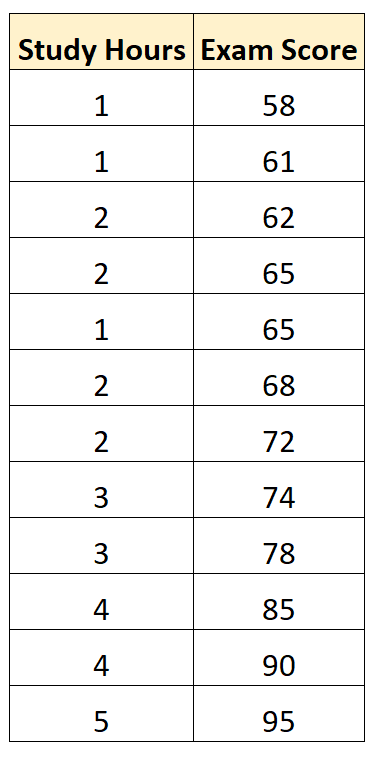
การใช้ซอฟต์แวร์ทางสถิติ (เช่น Excel, R, Python, SPSS ฯลฯ) เราสามารถติดตั้งแบบจำลองการถดถอยเชิงเส้นอย่างง่ายโดยใช้ “ชั่วโมงการศึกษา” เป็นตัวแปรทำนาย และ “เกรดการสอบ” เป็น ตัวแปรตอบสนอง

เราสามารถค้นหาผลลัพธ์ต่อไปนี้สำหรับรุ่นนี้:

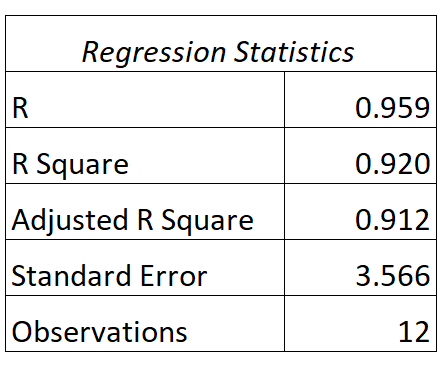
ต่อไปนี้เป็นวิธีการตีความค่า R และ R กำลังสองของแบบจำลองนี้:

• A: ความสัมพันธ์ระหว่างชั่วโมงเรียนกับคะแนนสอบคือ 0.959
• R ² : R กำลังสองสำหรับแบบจำลองการถดถอยนี้คือ 0.920 ข้อมูลนี้บอกเราว่า 92.0% ของความแปรผันของคะแนนสอบสามารถอธิบายได้ด้วยจำนวนชั่วโมงที่เรียน

โปรดทราบว่าค่า R ² นั้นเท่ากับค่า R โดยยกกำลังสอง:

^R2 = ร * ร = 0.959 * 0.959 = 0.920

ตัวอย่างที่ 2: การถดถอยเชิงเส้นพหุคูณ

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งแสดงชั่วโมงที่เรียน เกรดของนักเรียนปัจจุบัน และเกรดการสอบที่นักเรียน 12 คนได้รับในหลักสูตรคณิตศาสตร์บางหลักสูตร:

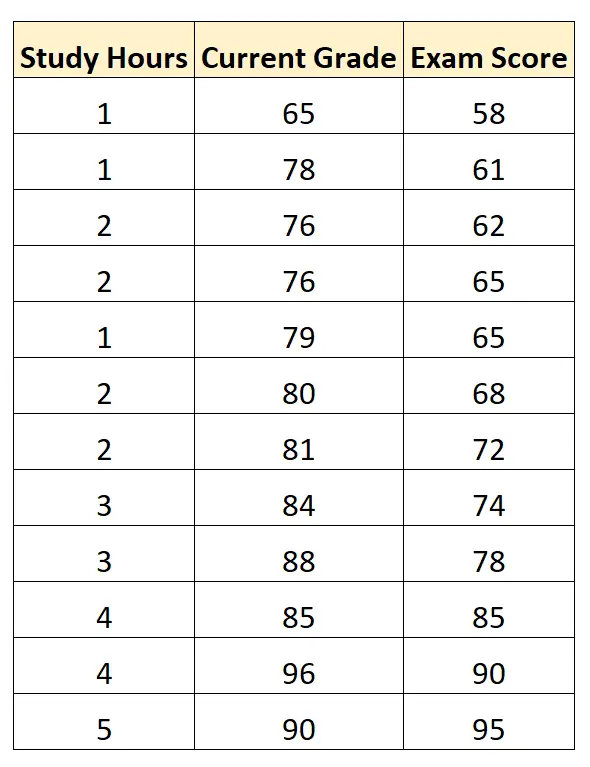
การใช้ซอฟต์แวร์ทางสถิติทำให้เราสามารถติดตั้งโมเดลการถดถอยเชิงเส้นหลายตัวได้โดยใช้ “ชั่วโมงการศึกษา” และ “เกรดปัจจุบัน” เป็นตัวแปรทำนาย และใช้ “เกรดการสอบ” เป็นตัวแปรตอบสนอง

เราสามารถค้นหาผลลัพธ์ต่อไปนี้สำหรับรุ่นนี้:

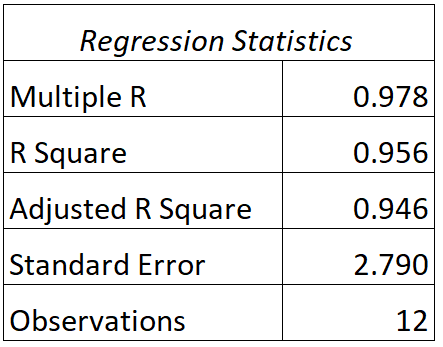
ต่อไปนี้เป็นวิธีการตีความค่า R และ R กำลังสองของแบบจำลองนี้:

• ตอบ: ความสัมพันธ์ระหว่างคะแนนการทดสอบจริงกับคะแนนการทดสอบที่คาดการณ์ไว้ของแบบจำลองคือ 0.978
• R ² : R กำลังสองสำหรับแบบจำลองการถดถอยนี้คือ 0.956 ข้อมูลนี้บอกเราว่า 95.6% ของการเปลี่ยนแปลงของคะแนนสอบสามารถอธิบายได้ด้วยจำนวนชั่วโมงที่เรียนและเกรดปัจจุบันของนักเรียนในชั้นเรียน

โปรดทราบว่าค่า R ² นั้นเท่ากับค่า R โดยยกกำลังสอง:

^R2 = ร * ร = 0.978 * 0.978 = 0.956

แหล่งข้อมูลเพิ่มเติม

ค่า R-กำลังสองที่ดีคืออะไร?
คำแนะนำอย่างอ่อนโยนเกี่ยวกับผลรวมของกำลังสอง: SST, SSR, SSE