Rmse กับ r-squared: คุณควรใช้เมตริกใด

แบบจำลองการถดถอยใช้ในการหาปริมาณความสัมพันธ์ระหว่างตัวแปรทำนายหนึ่งตัวขึ้นไปและตัวแปรตอบสนอง

เมื่อใดก็ตามที่เราปรับโมเดลการถดถอยให้เหมาะสม เราต้องการเข้าใจว่าโมเดล “เข้ากับ” ข้อมูลได้ดีเพียงใด กล่าวอีกนัยหนึ่งแบบจำลองสามารถใช้ค่าของตัวแปรทำนายเพื่อทำนายค่าของ ตัวแปรตอบสนอง ได้ดีแค่ไหน?

ตัวชี้วัดสองตัวที่นักสถิติมักใช้ในการวัดปริมาณว่าแบบจำลองเหมาะสมกับชุดข้อมูลได้ดีเพียงใด คือ ค่าคลาดเคลื่อนกำลังสองค่าเฉลี่ยราก (RMSE) และค่า R กำลังสอง ( ^R2 ) ซึ่งคำนวณได้ดังนี้:

RMSE : ตัวชี้วัดที่บอกเราว่าค่าที่ทำนายนั้นอยู่ห่างจากค่าที่สังเกตได้ในชุดข้อมูลโดยเฉลี่ยเท่าใด ยิ่ง RMSE ต่ำ โมเดลก็จะเหมาะกับชุดข้อมูลมากขึ้นเท่านั้น

มีการคำนวณดังนี้:

RMSE = √ Σ(พี _i – O _i ) ² / n

ทอง:

• Σ เป็นสัญลักษณ์ที่หมายถึง “ผลรวม”
• P _i คือค่าที่ทำนายไว้สำหรับการสังเกต ^{ครั้งที่ 3}
• O _i คือค่าที่สังเกตได้สำหรับการสังเกต ^{ที่ i}
• n คือขนาดตัวอย่าง

R ² : หน่วยเมตริกที่บอกเราว่าตัวแปรทำนายสามารถอธิบายความแปรปรวนในตัวแปรตอบสนองของแบบจำลองการถดถอยได้มากน้อยเพียงใด ค่านี้อยู่ระหว่าง 0 ถึง 1 ยิ่งค่า R ² สูง โมเดลก็จะเหมาะกับชุดข้อมูลมากขึ้นเท่านั้น

มีการคำนวณดังนี้:

^R2 = 1 – (RSS/TSS)

ทอง:

• RSS แสดงถึงผลรวมของกำลังสองของส่วนที่เหลือ
• TSS แสดงถึงผลรวมของกำลังสอง

RMSE กับ R ² : คุณควรใช้เมตริกใด

เมื่อประเมินความพอดีของแบบจำลองกับชุดข้อมูล การคำนวณ ทั้ง ค่า RMSE และค่า R ² จะมีประโยชน์ เนื่องจากแต่ละหน่วยเมตริกบอกเราบางอย่างที่แตกต่างกัน

ในแง่หนึ่ง RMSE บอกเราถึงระยะห่างโดยทั่วไประหว่างค่าที่ทำนายไว้โดยแบบจำลองการถดถอยกับค่าจริง

ในทางกลับกัน R ² บอกเราว่าตัวแปรทำนายสามารถอธิบายความแปรผันของตัวแปรตอบสนองได้มากเพียงใด

ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลต่อไปนี้ที่แสดงข้อมูลเกี่ยวกับบ้านในเมืองหนึ่งๆ:

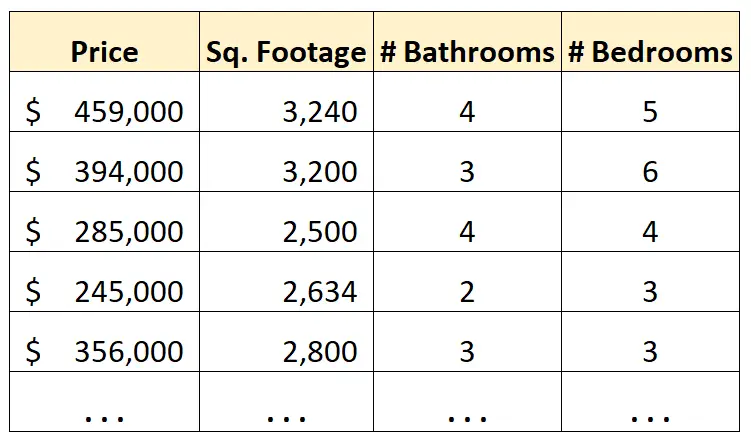
สมมติว่าเราต้องการใช้พื้นที่เป็นตารางฟุต จำนวนห้องน้ำ และจำนวนห้องนอนเพื่อทำนายราคาบ้าน

เราสามารถปรับโมเดลการถดถอยดังต่อไปนี้:

ราคา = β ₀ + β ₁ (พื้นที่เป็นตารางฟุต) + β ₂ (# ห้องน้ำ) + β ₃ (# ห้องนอน)

ตอนนี้ สมมติว่าเราพอดีกับโมเดลนี้ แล้วคำนวณหน่วยวัดต่อไปนี้เพื่อประเมินความดีของโมเดล:

• RMSE : 14.342
• ^R2 : 0.856

ค่า RMSE บอกเราว่าความแตกต่างโดยเฉลี่ยระหว่างราคาบ้านที่คาดการณ์ของแบบจำลองและราคาบ้านจริงคือ 14,342 ดอลลาร์

ค่า R ² บอกเราว่าตัวแปรทำนายของแบบจำลอง (พื้นที่เป็นตารางฟุต จำนวนห้องน้ำ และจำนวนห้องนอน) สามารถอธิบายการเปลี่ยนแปลงของราคาที่อยู่อาศัยได้ 85.6%

เพื่อพิจารณาว่าค่าเหล่านี้ “ดี” หรือไม่ เราสามารถเปรียบเทียบการวัดเหล่านี้กับรุ่นอื่นได้

ตัวอย่างเช่น สมมติว่าเราติดตั้งโมเดลการถดถอยอื่นที่ใช้ชุดตัวแปรทำนายที่แตกต่างกัน และคำนวณหน่วยเมตริกต่อไปนี้สำหรับโมเดลนั้น:

• RMSE : 19.355
• ^R2 : 0.765

เราจะเห็นว่าค่า RMSE ของรุ่นนี้สูงกว่ารุ่นก่อนๆ จะเห็นได้ว่าค่า R ² ของรุ่นนี้ยังต่ำกว่ารุ่นก่อนอีกด้วย สิ่งนี้บอกเราว่าแบบจำลองนี้เหมาะสมกับข้อมูลน้อยกว่ารุ่นก่อนหน้า

สรุป

นี่คือประเด็นหลักที่นำเสนอในบทความนี้:

• RMSE และ R ² จะวัดปริมาณว่าแบบจำลองการถดถอยเหมาะสมกับชุดข้อมูลเพียงใด
• RMSE บอกเราว่าแบบจำลองการถดถอยสามารถทำนายค่าของตัวแปรตอบสนองในรูปแบบสัมบูรณ์ได้ดีเพียงใด ในขณะที่ R ² บอกเราว่าแบบจำลองสามารถทำนายค่าของตัวแปรตอบสนองในรูปแบบเปอร์เซ็นต์ได้ดีเพียงใด
• การคำนวณทั้ง RMSE และ ^R2 สำหรับโมเดลที่กำหนดจะมีประโยชน์ เนื่องจากแต่ละเมตริกให้ข้อมูลที่เป็นประโยชน์แก่เรา

แหล่งข้อมูลเพิ่มเติม

รู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นพหุคูณ
R กับ R-Square: อะไรคือความแตกต่าง?
ค่า R-กำลังสองที่ดีคืออะไร?