วิธีการดำเนินการถดถอยเชิงเส้นหลายรายการใน spss

การถดถอยเชิงเส้นพหุคูณ เป็นวิธีการที่เราสามารถใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรอธิบายตั้งแต่สองตัวขึ้นไปกับตัวแปรตอบสนอง

บทช่วยสอนนี้จะอธิบายวิธีการถดถอยเชิงเส้นหลายรายการใน SPSS

ตัวอย่าง: การถดถอยเชิงเส้นพหุคูณใน SPSS

สมมติว่าเราต้องการทราบว่าจำนวนชั่วโมงในการเรียนและจำนวนข้อสอบฝึกหัดที่สอบส่งผลต่อเกรดที่นักเรียนได้รับจากการสอบที่กำหนดหรือไม่ เพื่อสำรวจสิ่งนี้ เราสามารถทำการถดถอยเชิงเส้นหลายรายการโดยใช้ตัวแปรต่อไปนี้:

ตัวแปรอธิบาย:

• ชั่วโมงการศึกษา
• การสอบเตรียมสอบผ่านแล้ว

ตัวแปรตอบสนอง:

• ผลสอบ

ใช้ขั้นตอนต่อไปนี้เพื่อดำเนินการการถดถอยเชิงเส้นหลายรายการใน SPSS

ขั้นตอนที่ 1: ป้อนข้อมูล

ป้อนข้อมูลต่อไปนี้สำหรับจำนวนชั่วโมงที่เรียน การสอบเตรียมสอบ และผลการสอบที่ได้รับสำหรับนักเรียน 20 คน:

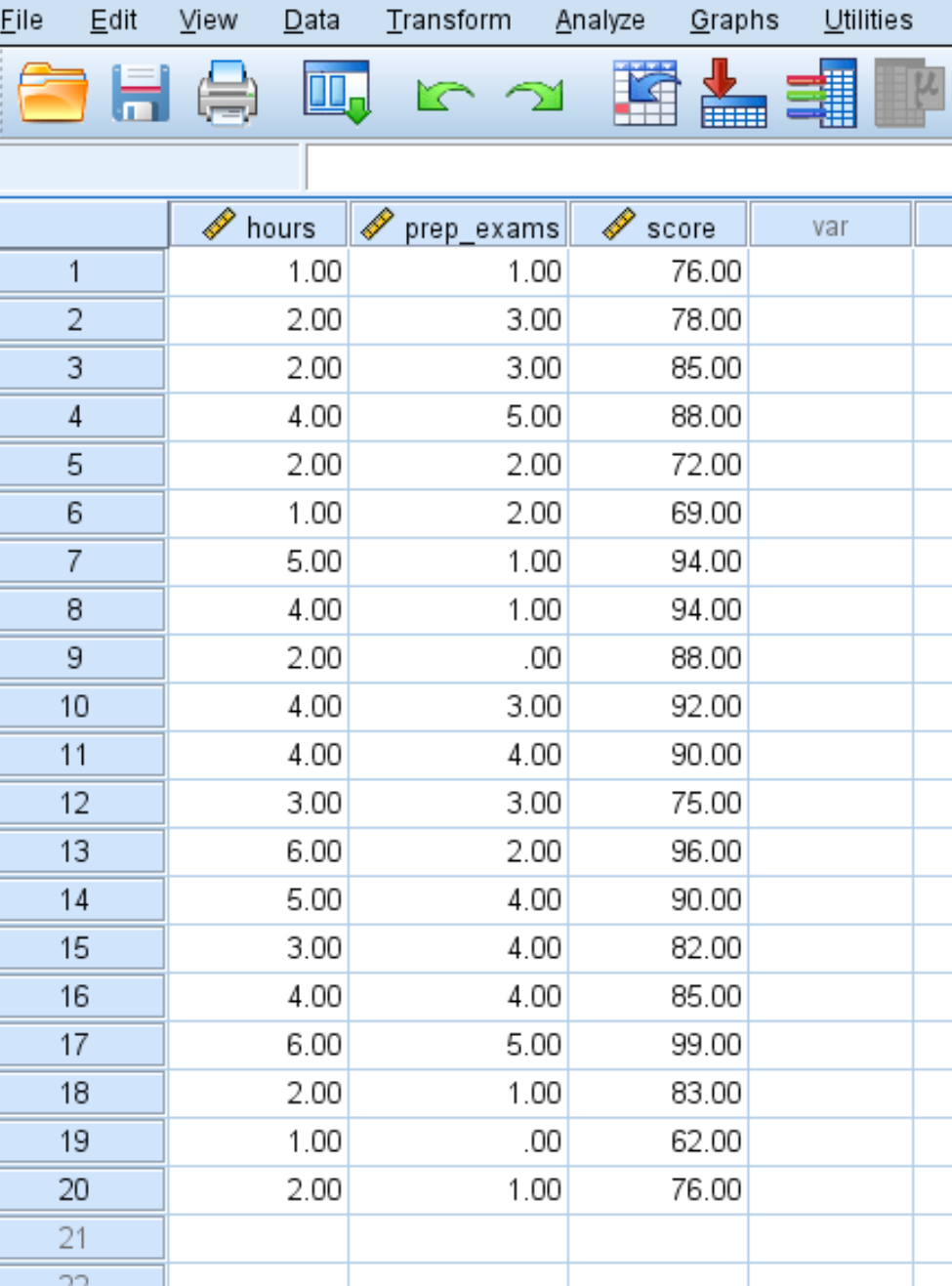
ขั้นตอนที่ 2: ดำเนินการถดถอยเชิงเส้นหลายรายการ

คลิกแท็บ วิเคราะห์ จากนั้นคลิก Regression จากนั้นคลิก Linear :

ลาก คะแนน ตัวแปรลงในกล่องที่มีข้อความว่าขึ้นอยู่กับ ลากตัวแปร ชั่วโมง และ prep_exams ลงในช่องที่มีป้ายกำกับ Independent(s) จากนั้นคลิก ตกลง

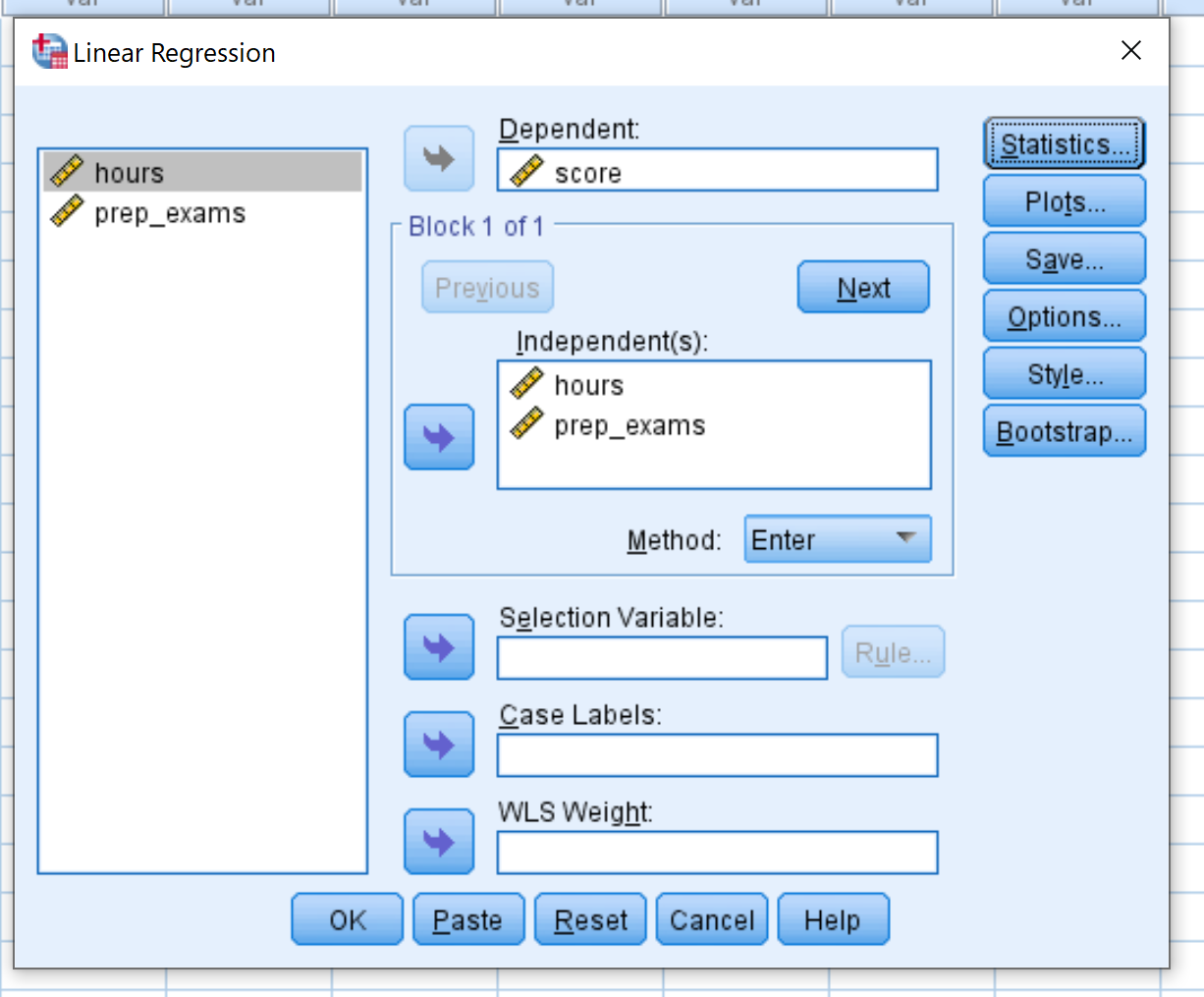
ขั้นตอนที่ 3: ตีความผลลัพธ์

เมื่อคุณคลิก ตกลง ผลลัพธ์การถดถอยเชิงเส้นหลายรายการจะปรากฏในหน้าต่างใหม่

ตารางแรกที่เราสนใจเรียกว่า Model Summary :

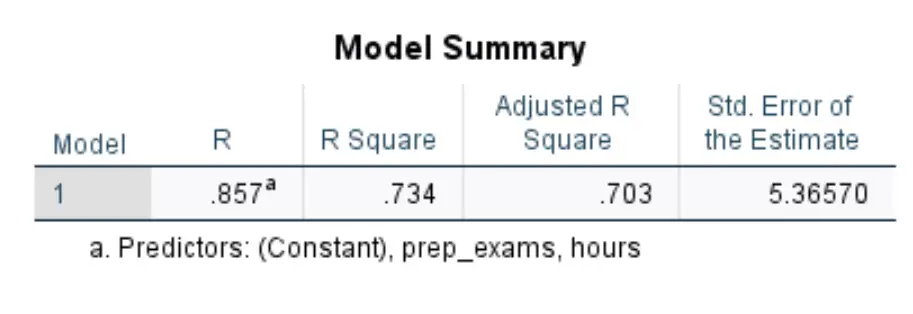
ต่อไปนี้เป็นวิธีการตีความตัวเลขที่เกี่ยวข้องมากที่สุดในตารางนี้:

• R Square: นี่คือสัดส่วนของความแปรปรวนในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรอธิบาย ในตัวอย่างนี้ 73.4% ของการเปลี่ยนแปลงของคะแนนสอบสามารถอธิบายได้ด้วยจำนวนชั่วโมงเรียนและจำนวนการสอบเพื่อเตรียมสอบ
• มาตรฐาน. ข้อผิดพลาดในการประมาณค่า: ข้อผิดพลาดมาตรฐาน คือระยะห่างเฉลี่ยระหว่างค่าที่สังเกตได้กับเส้นการถดถอย ในตัวอย่างนี้ ค่าที่สังเกตได้เบี่ยงเบนโดยเฉลี่ย 5.3657 หน่วยจากเส้นถดถอย

ตารางถัดไปที่เราสนใจเรียกว่า ANOVA :

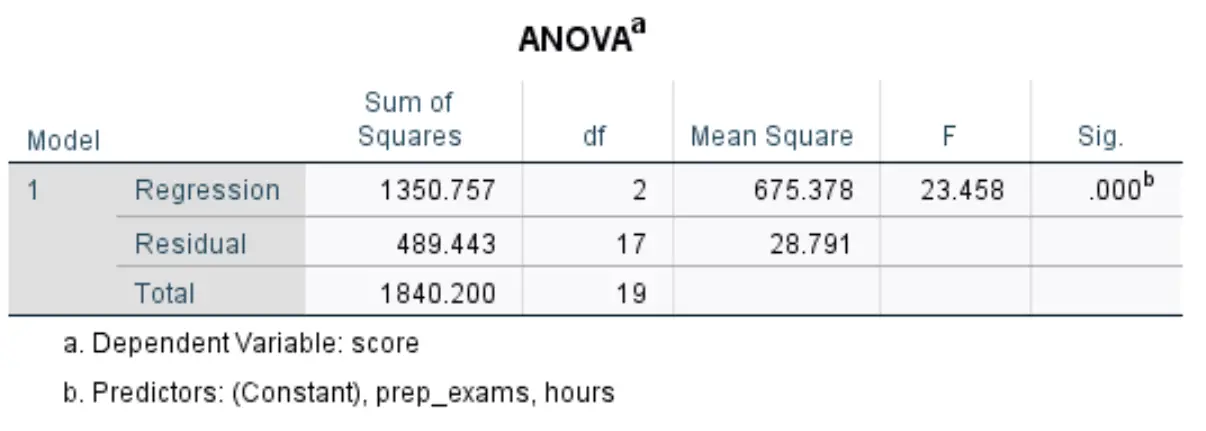
ต่อไปนี้เป็นวิธีการตีความตัวเลขที่เกี่ยวข้องมากที่สุดในตารางนี้:

• F: นี่คือสถิติ F โดยรวมสำหรับแบบจำลองการถดถอย ซึ่งคำนวณเป็น Mean Square Regression / Mean Square Residual
• Sig: นี่คือค่า p ที่เกี่ยวข้องกับสถิติ F โดยรวม ข้อมูลนี้บอกเราว่าแบบจำลองการถดถอยโดยรวมมีนัยสำคัญทางสถิติหรือไม่ กล่าวอีกนัยหนึ่ง มันบอกเราว่าตัวแปรอธิบายสองตัวที่รวมกันมีความสัมพันธ์ที่มีนัยสำคัญทางสถิติกับตัวแปรตอบสนองหรือไม่ ในกรณีนี้ ค่า p เท่ากับ 0.000 ซึ่งบ่งชี้ว่าตัวแปรอธิบาย ชั่วโมงการศึกษา และการสอบเตรียมสอบ มีความสัมพันธ์ที่มีนัยสำคัญทางสถิติกับผลการสอบ

ตารางต่อไปนี้ที่เราสนใจมีชื่อว่า ค่าสัมประสิทธิ์ :

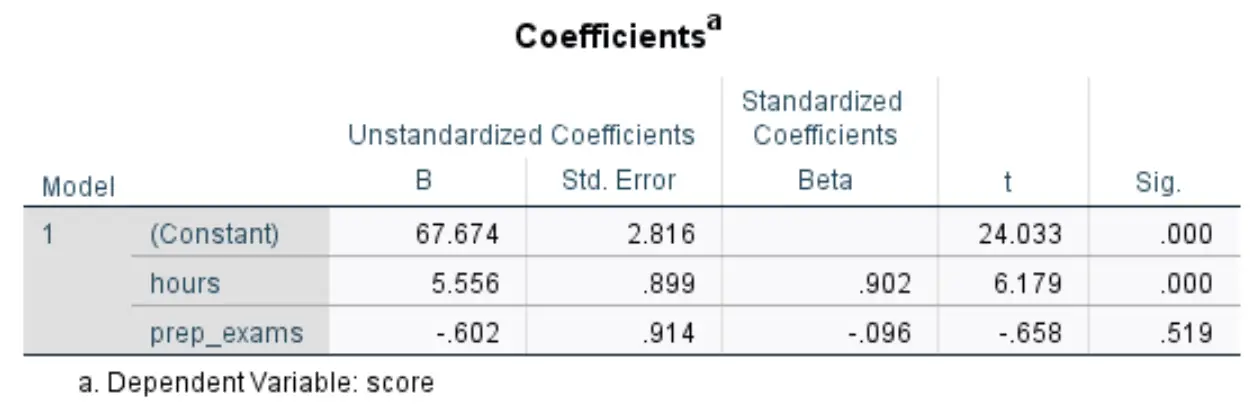
ต่อไปนี้เป็นวิธีการตีความตัวเลขที่เกี่ยวข้องมากที่สุดในตารางนี้:

• B ไม่ได้มาตรฐาน (คงที่): สิ่งนี้บอกเราถึงค่าเฉลี่ยของตัวแปรตอบสนองเมื่อตัวแปรทำนายทั้งสองมีค่าเป็นศูนย์ ในตัวอย่างนี้ คะแนนสอบเฉลี่ยคือ 67,674 เมื่อชั่วโมงเรียนและการสอบเตรียมอุดมศึกษาเป็นศูนย์ทั้งคู่
• B ที่ไม่ได้มาตรฐาน (ชั่วโมง): ข้อมูลนี้บอกเราถึงการเปลี่ยนแปลงโดยเฉลี่ยของคะแนนสอบที่เกี่ยวข้องกับการเพิ่มชั่วโมงเรียนหนึ่งหน่วย โดยสมมติว่าจำนวนการสอบเตรียมสอบคงที่ ในกรณีนี้ แต่ละชั่วโมงที่เรียนเพิ่มเติมจะสัมพันธ์กับคะแนนสอบที่เพิ่มขึ้น 5,556 คะแนน โดยสมมติว่าจำนวนข้อสอบฝึกหัดที่สอบคงที่
• B ที่ไม่เป็นไปตามมาตรฐาน (prep_exams): ข้อมูลนี้บอกเราถึงการเปลี่ยนแปลงโดยเฉลี่ยของคะแนนสอบที่เกี่ยวข้องกับการสอบเตรียมสอบที่เพิ่มขึ้นหนึ่งหน่วย โดยสมมติว่าจำนวนชั่วโมงที่ศึกษายังคงที่ ในกรณีนี้ การสอบเพื่อเตรียมการเพิ่มเติมแต่ละครั้งที่สอบจะสัมพันธ์กับคะแนนสอบที่ลดลง 0.602 คะแนน โดยสมมติว่าจำนวนชั่วโมงที่เรียนคงที่
• ซิก (ชั่วโมง): นี่คือค่า p สำหรับ ชั่วโมง ตัวแปรอธิบาย เนื่องจากค่านี้ (0.000) น้อยกว่า 0.05 เราจึงสามารถสรุปได้ว่าจำนวนชั่วโมงที่เรียนมีความสัมพันธ์ที่มีนัยสำคัญทางสถิติกับคะแนนสอบ
• ซิก (prep_exams): นี่คือค่า p สำหรับตัวแปรอธิบาย prep_exams เนื่องจากค่านี้ (0.519) ไม่น้อยกว่า 0.05 เราจึงไม่สามารถสรุปได้ว่าจำนวนการสอบเพื่อเตรียมความพร้อมที่ดำเนินการมีความสัมพันธ์ที่มีนัยสำคัญทางสถิติกับผลการสอบ

สุดท้ายนี้ เราสามารถสร้างสมการการถดถอยโดยใช้ค่าที่แสดงในตารางสำหรับ ค่าคงที่ ชั่วโมง และ prep_exams ในกรณีนี้ สมการจะเป็นดังนี้:

คะแนนสอบโดยประมาณ = 67.674 + 5.556*(ชั่วโมง) – 0.602*(prep_exams)

เราสามารถใช้สมการนี้เพื่อหาคะแนนสอบโดยประมาณของนักเรียน โดยพิจารณาจากจำนวนชั่วโมงเรียนและจำนวนข้อสอบฝึกหัดที่พวกเขาทำ ตัวอย่างเช่น นักเรียนที่เรียน 3 ชั่วโมง และสอบเตรียมสอบ 2 ครั้ง ควรได้คะแนนสอบ 83.1:

คะแนนสอบโดยประมาณ = 67.674 + 5.556*(3) – 0.602*(2) = 83.1

หมายเหตุ: เนื่องจากไม่พบว่าตัวแปรอธิบาย สำหรับการสอบเตรียมสอบ มีนัยสำคัญทางสถิติ เราจึงสามารถตัดสินใจลบตัวแปรดังกล่าวออกจากแบบจำลองและดำเนิน การการถดถอยเชิงเส้นอย่างง่าย แทนโดยใช้ ชั่วโมงที่ศึกษา เป็นตัวแปรอธิบายเพียงตัวเดียว