วิธีสร้างเมทริกซ์ความแปรปรวนร่วมใน spss

ความแปรปรวนร่วม คือการวัดว่าการเปลี่ยนแปลงในตัวแปรหนึ่งสัมพันธ์กับการเปลี่ยนแปลงในตัวแปรตัวที่สองอย่างไร โดยเฉพาะอย่างยิ่ง มันคือการวัดระดับที่ตัวแปรสองตัวมีความสัมพันธ์กันเชิงเส้นตรง

สูตรคำนวณความแปรปรวนร่วมระหว่างตัวแปรสองตัว X และ Y คือ:

COV( X , Y ) = Σ(x- x )(y- y ) / n

เมทริกซ์ความแปรปรวนร่วม คือเมทริกซ์จตุรัสที่แสดงความแปรปรวนร่วมระหว่างตัวแปรต่างๆ ในชุดข้อมูล

บทช่วยสอนนี้จะอธิบายวิธีสร้างเมทริกซ์ความแปรปรวนร่วมสำหรับชุดข้อมูลที่ระบุใน SPSS

ตัวอย่าง: เมทริกซ์ความแปรปรวนร่วมใน SPSS

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ที่แสดงคะแนนสอบของนักเรียนที่แตกต่างกัน 10 คนใน 3 วิชา: คณิตศาสตร์ วิทยาศาสตร์ และประวัติศาสตร์:

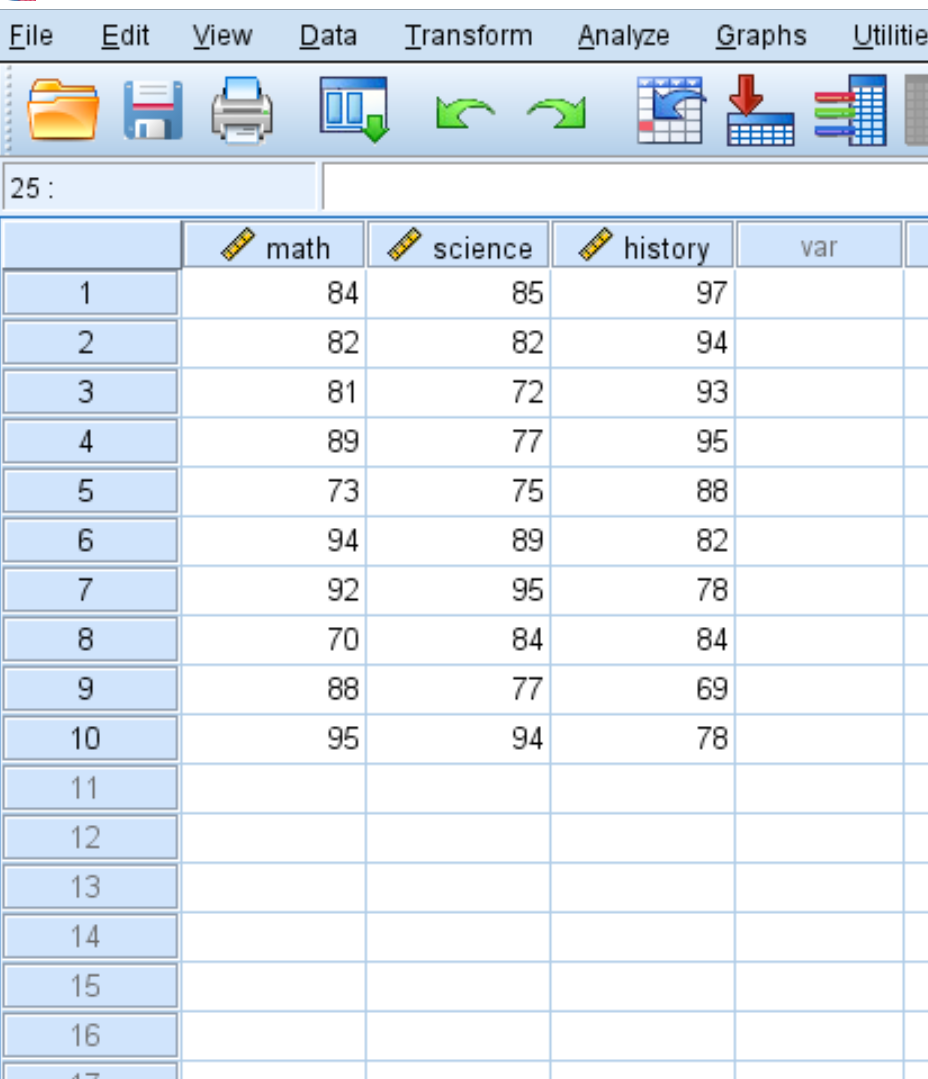
หากต้องการสร้างเมทริกซ์ความแปรปรวนร่วมสำหรับชุดข้อมูลนี้ คลิกแท็บ วิเคราะห์ จากนั้นคลิก ความสัมพันธ์ จากนั้น เปลี่ยนตัวแปร :

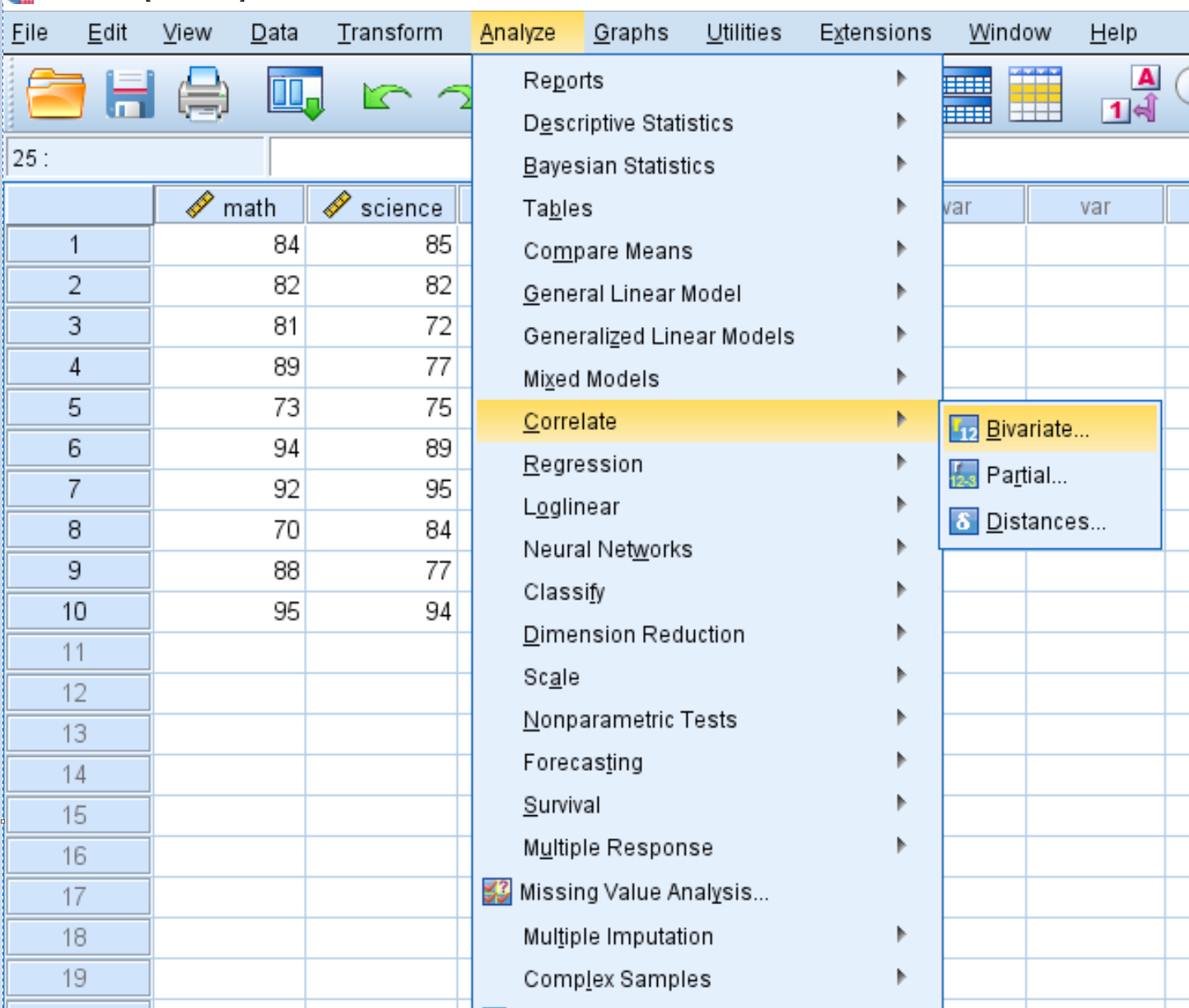
ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ลากตัวแปรทั้งสามตัวลงในช่องที่มีข้อความ Variables :

จากนั้นคลิก ตัวเลือก ทำเครื่องหมายที่ช่องถัดจาก ผลต่างและความแปรปรวนร่วมระหว่างผลิตภัณฑ์ จากนั้นคลิก ดำเนินการต่อ

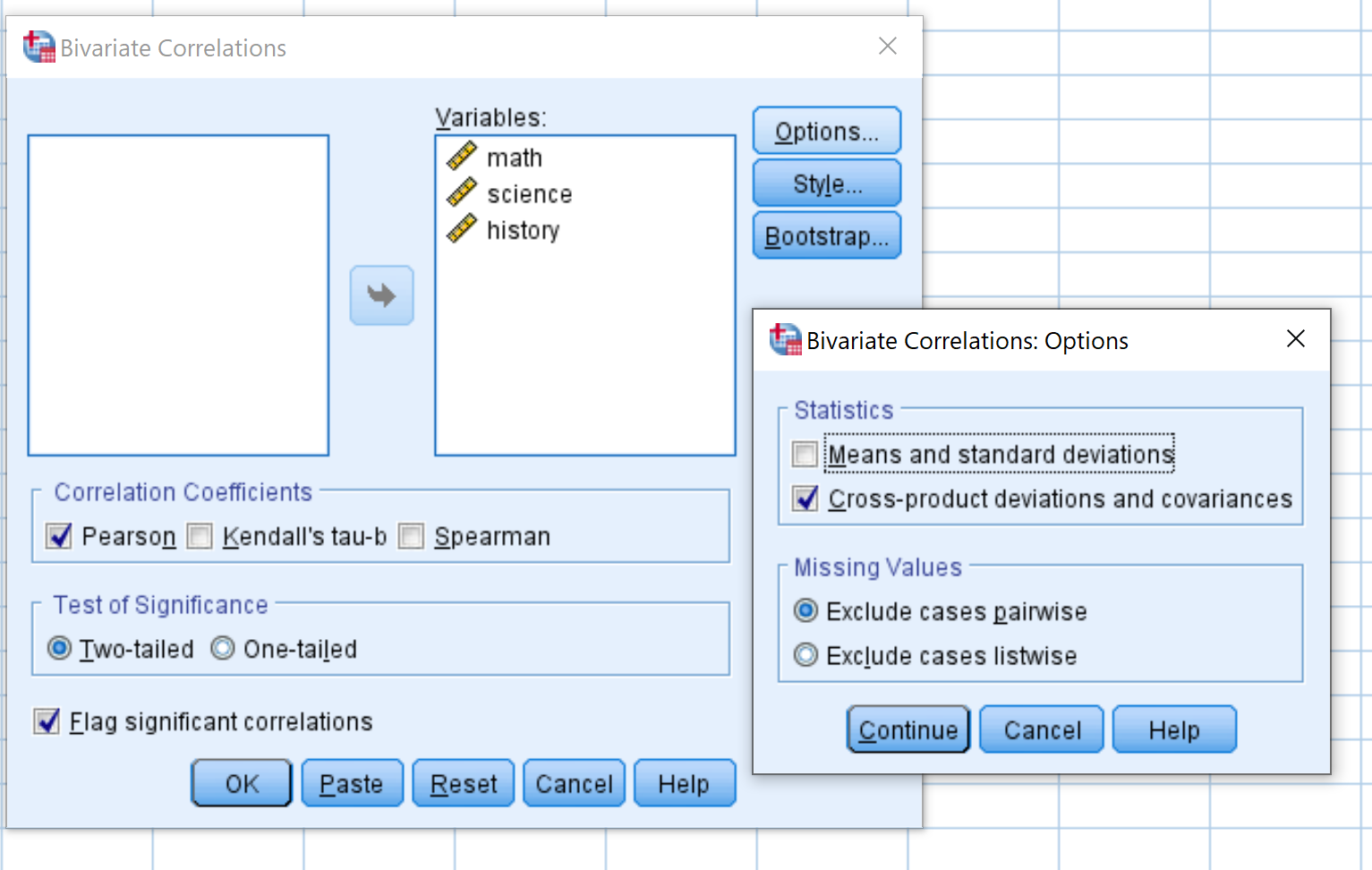
จากนั้นคลิก ตกลง ผลลัพธ์จะปรากฏในหน้าต่างใหม่:

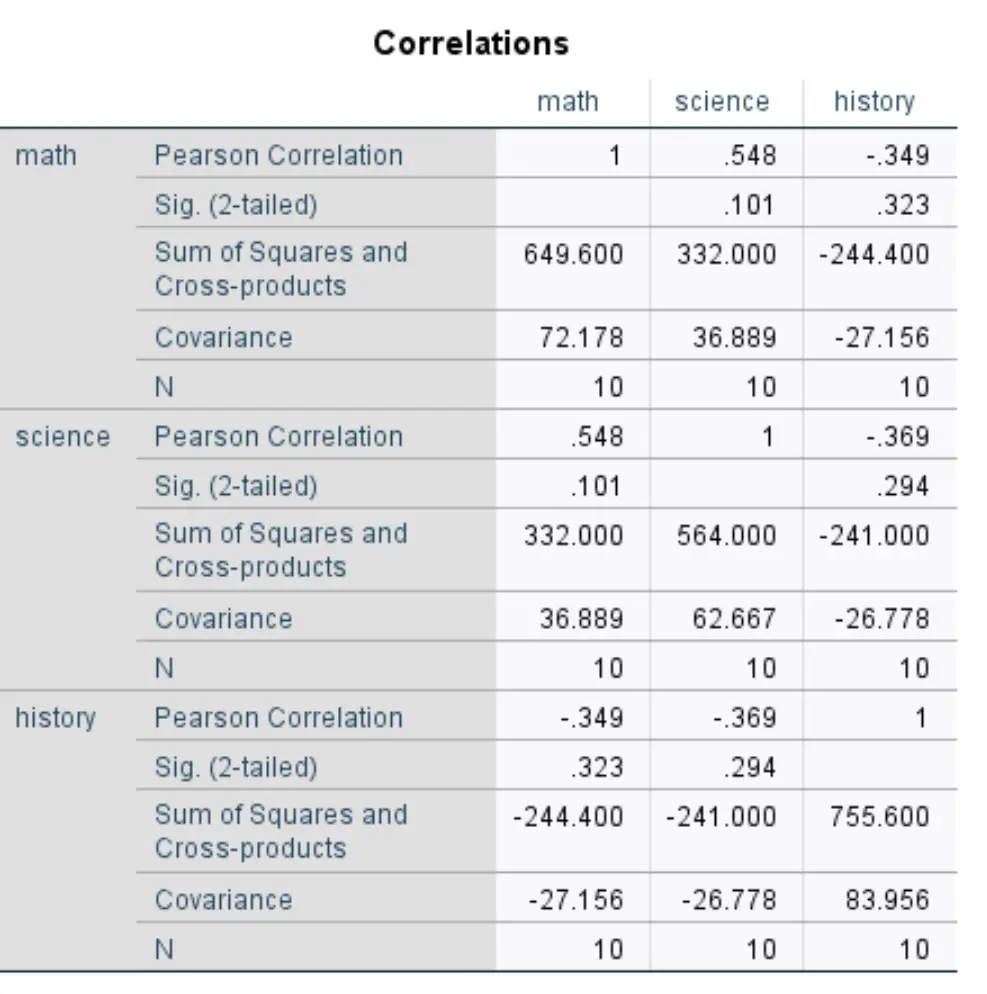
หากต้องการหาค่าความแปรปรวนร่วมสำหรับการผสมตัวแปรแต่ละคู่ คุณต้องหาร ผลรวมของกำลังสองและผลิตภัณฑ์เวกเตอร์ ด้วย N

ตัวอย่างเช่น สามารถคำนวณความแปรปรวนร่วมระหว่างคณิตศาสตร์และวิทยาศาสตร์ได้ดังนี้:

COV (คณิต วิทยาศาสตร์) = 332,000 / 10 = 33.2

ในทำนองเดียวกัน สามารถคำนวณความแปรปรวนร่วมระหว่างคณิตศาสตร์และประวัติศาสตร์ได้ดังนี้

COV (คณิตศาสตร์ ประวัติศาสตร์) = -244.400 / 10 = -24.44

คุณยังสามารถรับความแปรปรวนของตัวแปรแต่ละตัวได้โดยการหาร ผลรวมของกำลังสองและผลิตภัณฑ์เวกเตอร์ ด้วย N

ตัวอย่างเช่น ความแปรปรวนทางคณิตศาสตร์สามารถคำนวณได้ดังนี้:

VAR(คณิตศาสตร์) = 649.600 / 10 = 64.96 .

คุณสามารถรับเมทริกซ์ความแปรปรวนร่วมแบบเต็มสำหรับชุดข้อมูลนี้ได้โดยการคำนวณที่คล้ายกัน:

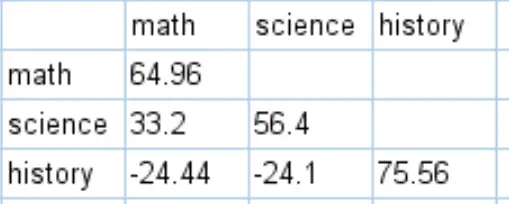
วิธีการตีความเมทริกซ์ความแปรปรวนร่วม

ค่าตามเส้นทแยงมุมของเมทริกซ์ความแปรปรวนร่วมเป็นเพียงความแปรปรวนของแต่ละเรื่อง ตัวอย่างเช่น:

• ความแปรปรวนของผลลัพธ์ทางคณิตศาสตร์คือ 64.96
• ความแปรปรวนของคะแนนวิทยาศาสตร์คือ 56.4
• ความแปรปรวนของคะแนนในอดีตคือ 75.56

ค่าอื่นๆ ของเมทริกซ์แสดงถึงความแปรปรวนร่วมระหว่างวิชาต่างๆ ตัวอย่างเช่น:

• ความแปรปรวนร่วมระหว่างคะแนนคณิตศาสตร์และวิทยาศาสตร์คือ 33.2
• ความแปรปรวนร่วมระหว่างคะแนนคณิตศาสตร์และประวัติศาสตร์คือ -24.44
• ความแปรปรวนร่วมระหว่างคะแนนวิทยาศาสตร์และประวัติศาสตร์คือ -24.1

จำนวนบวก สำหรับความแปรปรวนร่วมบ่งชี้ว่าตัวแปรสองตัวมีแนวโน้มเพิ่มขึ้นหรือลดลงตามกัน ตัวอย่างเช่น คณิตศาสตร์และวิทยาศาสตร์มีความแปรปรวนร่วมเชิงบวก (33.2) ซึ่งบ่งชี้ว่านักเรียนที่ได้คะแนนสูงในวิชาคณิตศาสตร์ก็มีแนวโน้มที่จะได้คะแนนสูงในวิชาวิทยาศาสตร์เช่นกัน ในทำนองเดียวกัน นักเรียนที่มีผลการเรียนไม่ดีในวิชาคณิตศาสตร์ก็มักจะมีผลการเรียนไม่ดีในวิชาวิทยาศาสตร์เช่นกัน

จำนวนลบ สำหรับความแปรปรวนร่วมบ่งชี้ว่าเมื่อตัวแปรตัวหนึ่งเพิ่มขึ้น ตัวแปรตัวที่สองมีแนวโน้มลดลง ตัวอย่างเช่น วิทยาศาสตร์และประวัติศาสตร์มีความแปรปรวนร่วมเป็นลบ (-24.1) ซึ่งบ่งชี้ว่านักเรียนที่ได้คะแนนสูงในด้านวิทยาศาสตร์มักจะได้คะแนนต่ำในประวัติศาสตร์ ในทำนองเดียวกัน นักเรียนที่ได้คะแนนต่ำในด้านวิทยาศาสตร์มักจะได้คะแนนสูงในประวัติศาสตร์

แหล่งข้อมูลเพิ่มเติม

วิธีสร้างเมทริกซ์สหสัมพันธ์ใน SPSS
วิธีการคำนวณความสัมพันธ์บางส่วนใน SPSS