วิธีดำเนินการถดถอยกำลังสองใน spss

เมื่อตัวแปรสองตัวมีความสัมพันธ์เชิงเส้น คุณมักจะใช้ การถดถอยเชิงเส้นอย่างง่าย เพื่อหาปริมาณความสัมพันธ์ได้

อย่างไรก็ตาม การถดถอยเชิงเส้นอย่างง่ายทำงานได้ไม่ดีเมื่อตัวแปรสองตัวมีความสัมพันธ์แบบไม่เชิงเส้น ในกรณีเหล่านี้ คุณสามารถลองใช้ การถดถอยกำลังสองได้

บทช่วยสอนนี้จะอธิบายวิธีการถดถอยกำลังสองใน SPSS

ตัวอย่าง: การถดถอยกำลังสองใน SPSS

สมมติว่าเราต้องการเข้าใจความสัมพันธ์ระหว่างจำนวนชั่วโมงทำงานกับความสุข เรามีข้อมูลเกี่ยวกับจำนวนชั่วโมงทำงานต่อสัปดาห์และรายงานระดับความสุข (ในระดับ 0 ถึง 100) สำหรับคน 16 คนดังต่อไปนี้:

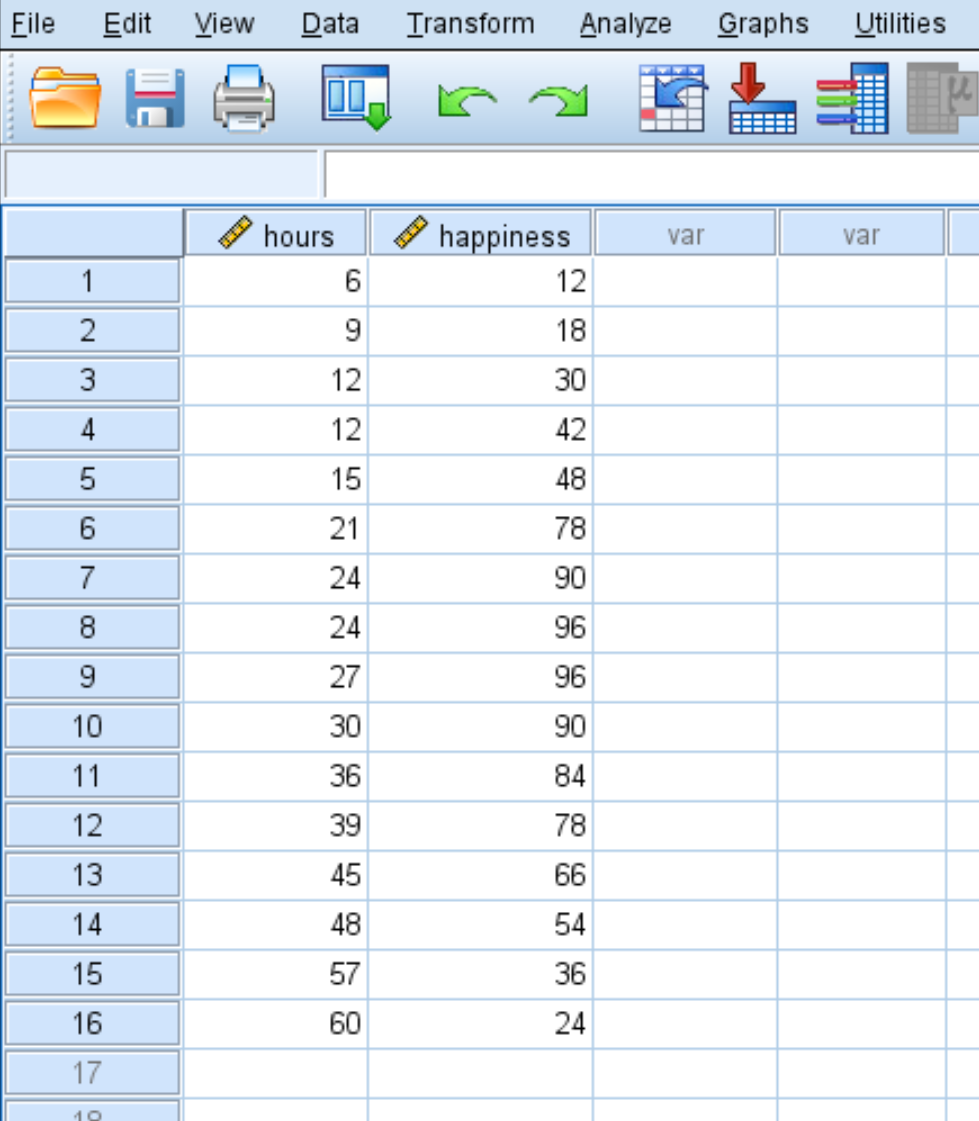
ใช้ขั้นตอนต่อไปนี้เพื่อดำเนินการถดถอยกำลังสองใน SPSS

ขั้นตอนที่ 1: แสดงภาพข้อมูล

ก่อนที่จะทำการถดถอยกำลังสอง เรามาสร้างแผนภาพกระจายเพื่อแสดงความสัมพันธ์ระหว่างชั่วโมงทำงานและความสุขก่อน เพื่อตรวจสอบว่าตัวแปรทั้งสองมีความสัมพันธ์กันในสมการกำลังสองจริงๆ

คลิกแท็บ แผนภูมิ จากนั้น คลิกตัวสร้างแผนภูมิ :

ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้เลือก กระจาย/จุด จากรายการ เลือกจาก จากนั้นลากแผนภูมิชื่อ Simple Scatter ลงในหน้าต่างแก้ไขหลัก ลาก ชั่วโมง แปรผันบนแกน x และ ลากความสุข บนแกน y จากนั้นคลิก ตกลง

แผนภาพกระจายต่อไปนี้จะปรากฏขึ้น:

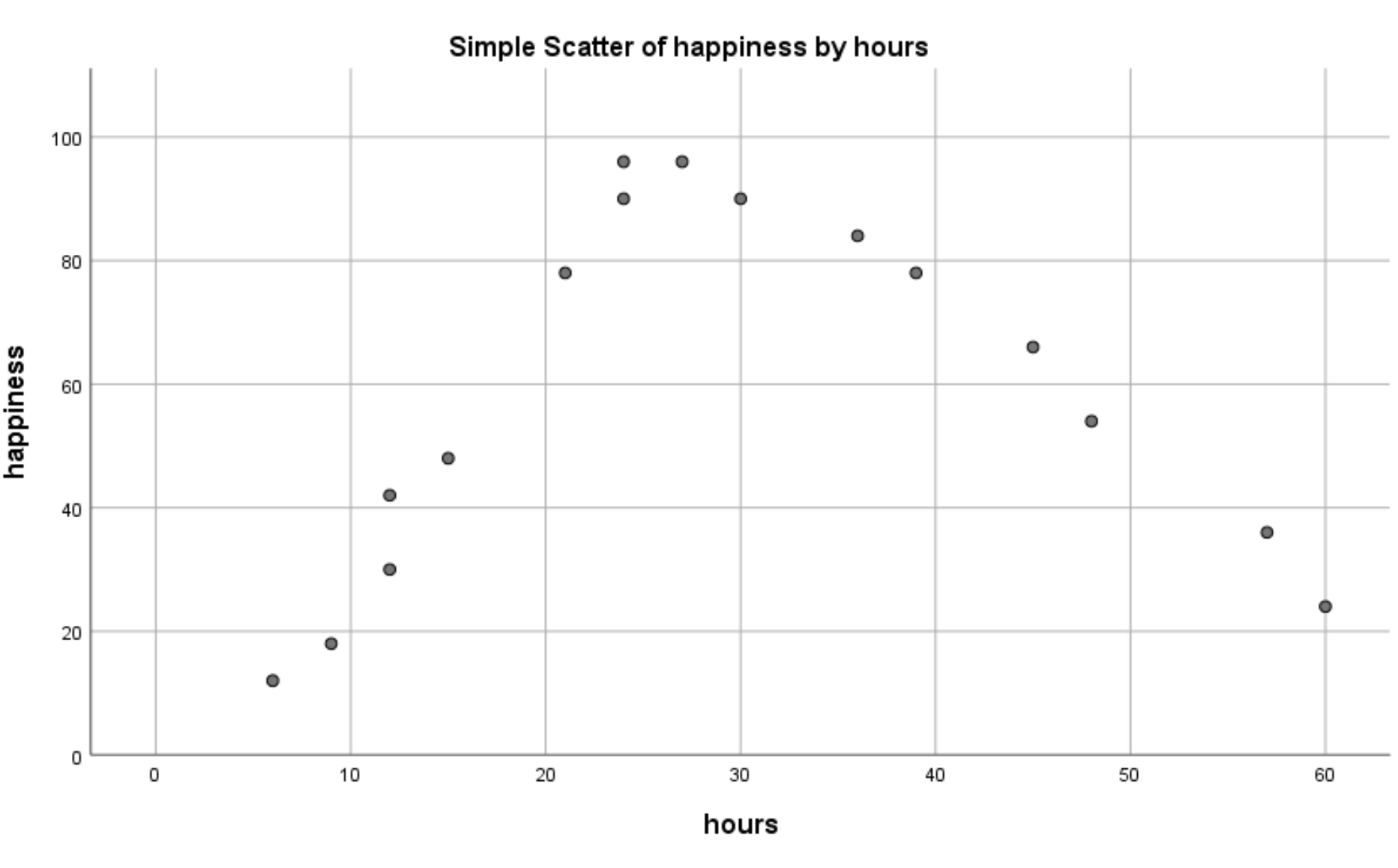
เราจะเห็นได้อย่างชัดเจนว่ามีความสัมพันธ์แบบไม่เชิงเส้นระหว่างชั่วโมงทำงานกับความสุข สิ่งนี้บอกเราว่าการถดถอยกำลังสองเป็นเทคนิคที่เหมาะสมที่จะใช้ในสถานการณ์นี้

ขั้นตอนที่ 2: สร้างตัวแปรใหม่

ก่อนที่เราจะทำการถดถอยกำลังสองได้ เราต้องสร้างตัวแปรทำนายสำหรับชั่วโมง ² ก่อน

คลิกแท็บ การแปลง จากนั้น คลิกคำนวณตัวแปร :

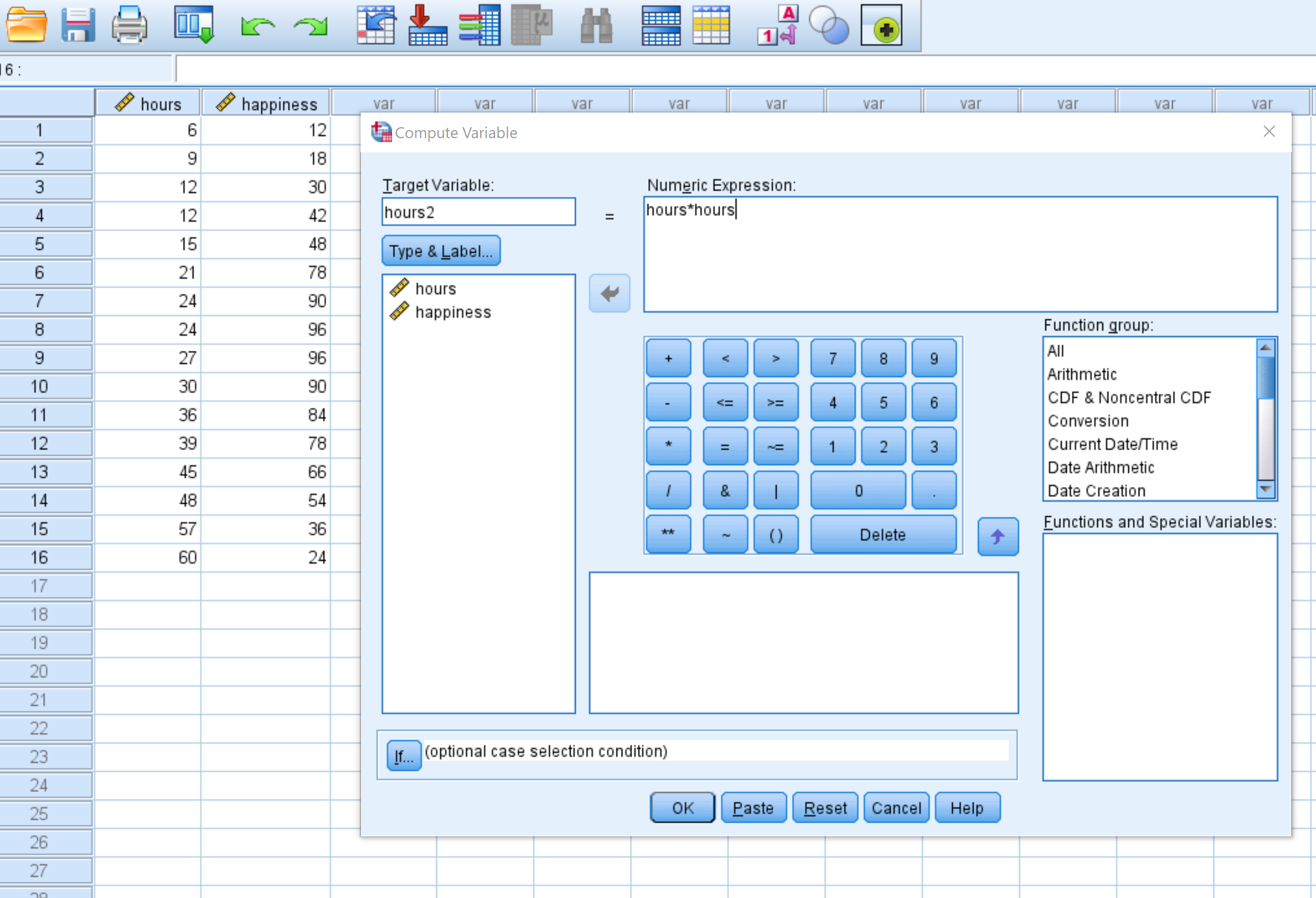
ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ตั้งชื่อตัวแปรเป้าหมาย hour2 และตั้งค่าเป็น hour*hour :

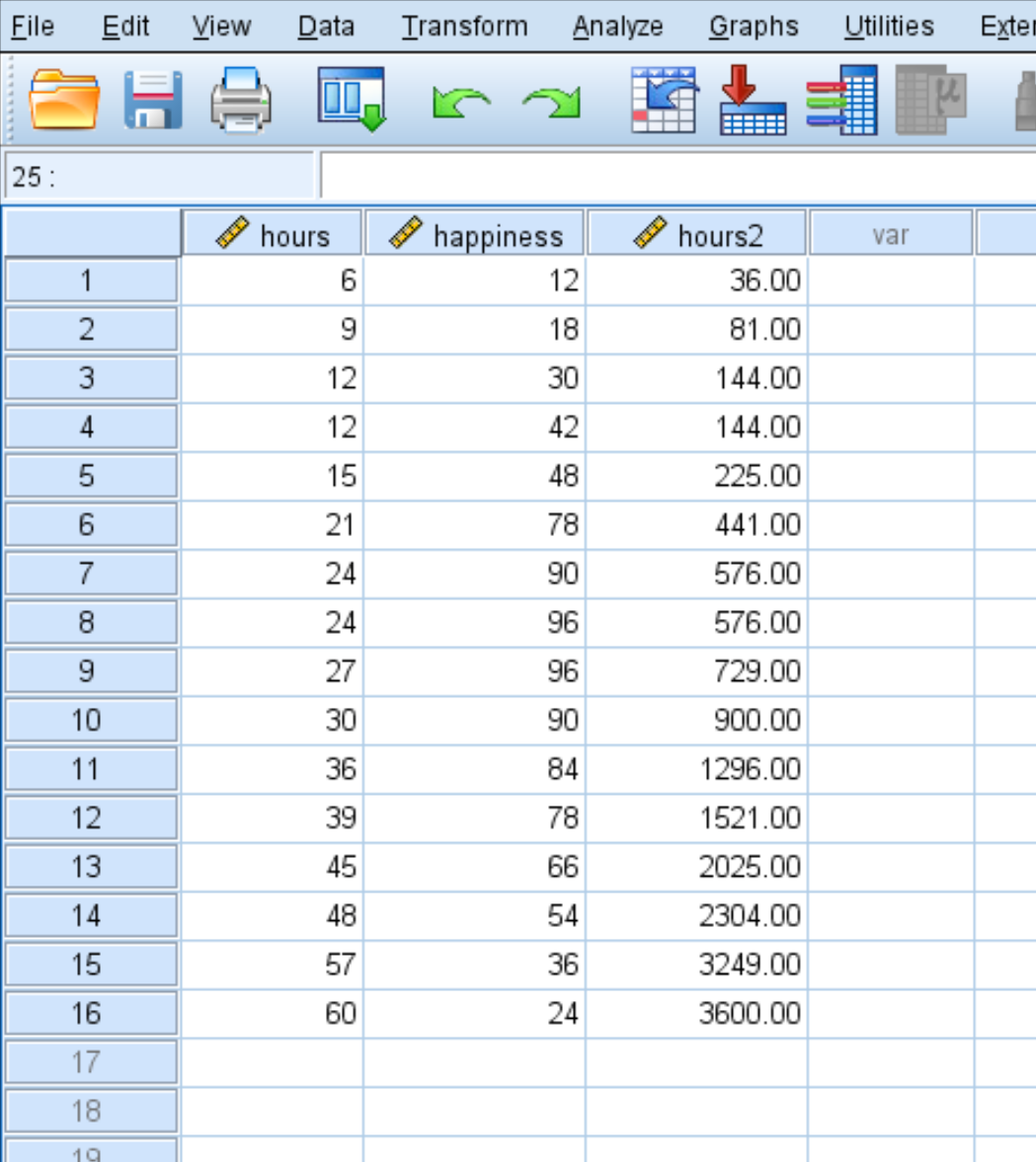
เมื่อคุณคลิก OK ตัวแปร hour2 จะปรากฏในคอลัมน์ใหม่:

ขั้นตอนที่ 3: ดำเนินการถดถอยกำลังสอง

ต่อไป เราจะทำการถดถอยกำลังสอง คลิกแท็บ วิเคราะห์ จากนั้นคลิก Regression จากนั้นคลิก Linear :

ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ลาก ความสุข ลงในกล่องที่มีข้อความว่าขึ้นอยู่กับ ลาก ชั่วโมง และ ชั่วโมง2 ลงในกล่องที่มีข้อความเป็นอิสระ จากนั้นคลิก ตกลง

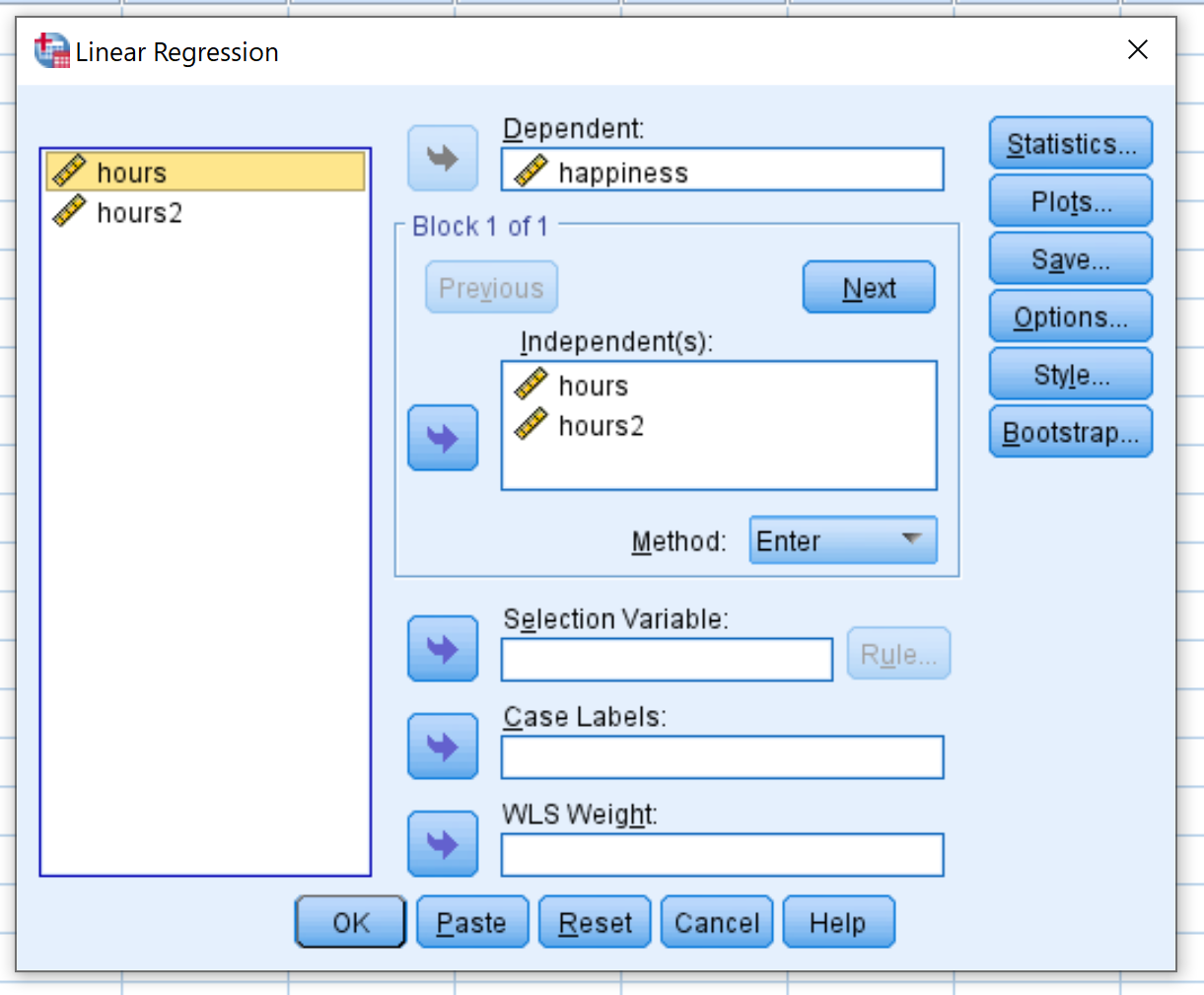
ขั้นตอนที่ 4: ตีความผลลัพธ์

เมื่อคุณคลิก ตกลง ผลลัพธ์การถดถอยกำลังสองจะปรากฏในหน้าต่างใหม่

ตารางแรกที่เราสนใจเรียกว่า Model Summary :

ต่อไปนี้เป็นวิธีการตีความตัวเลขที่เกี่ยวข้องมากที่สุดในตารางนี้:

• R Square: นี่คือสัดส่วนของความแปรปรวนในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรอธิบาย ในตัวอย่างนี้ ความแปรผันของความสุข 90.9% สามารถอธิบายได้ด้วยตัวแปร ชั่วโมง และ ชั่วโมง ²
• มาตรฐาน. ข้อผิดพลาดในการประมาณค่า: ข้อผิดพลาดมาตรฐาน คือระยะห่างเฉลี่ยระหว่างค่าที่สังเกตได้กับเส้นการถดถอย ในตัวอย่างนี้ ค่าที่สังเกตได้เบี่ยงเบนไปจากเส้นถดถอยโดยเฉลี่ย 9,519 หน่วย

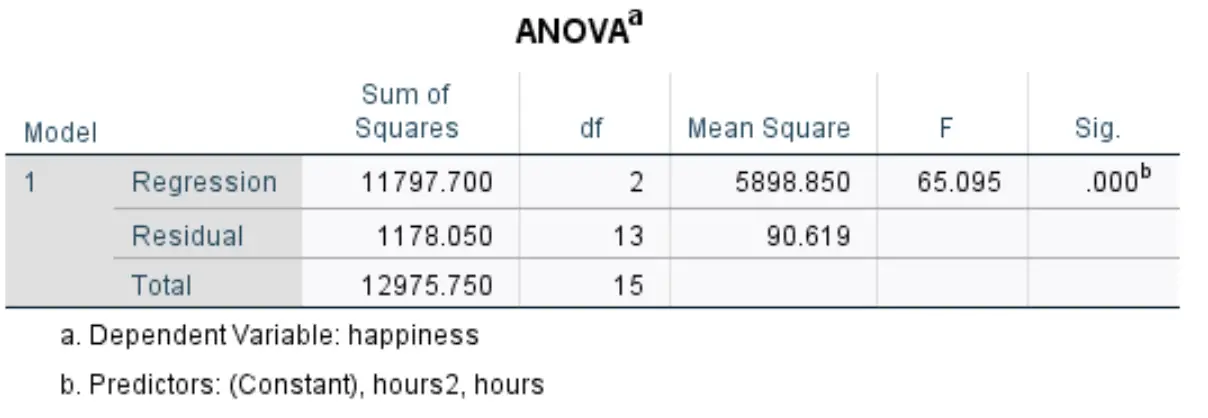
ตารางถัดไปที่เราสนใจเรียกว่า ANOVA :

ต่อไปนี้เป็นวิธีการตีความตัวเลขที่เกี่ยวข้องมากที่สุดในตารางนี้:

• F: นี่คือสถิติ F โดยรวมสำหรับแบบจำลองการถดถอย ซึ่งคำนวณเป็น Mean Square Regression / Mean Square Residual
• Sig: นี่คือค่า p ที่เกี่ยวข้องกับสถิติ F โดยรวม ข้อมูลนี้บอกเราว่าแบบจำลองการถดถอยโดยรวมมีนัยสำคัญทางสถิติหรือไม่ ในกรณีนี้ ค่า p เท่ากับ 0.000 ซึ่งบ่งชี้ว่าตัวแปรอธิบาย ชั่วโมง และ ชั่วโมง ² รวมกันมีความสัมพันธ์ที่มีนัยสำคัญทางสถิติกับผลการสอบ

ตารางต่อไปนี้ที่เราสนใจมีชื่อว่า ค่าสัมประสิทธิ์ :

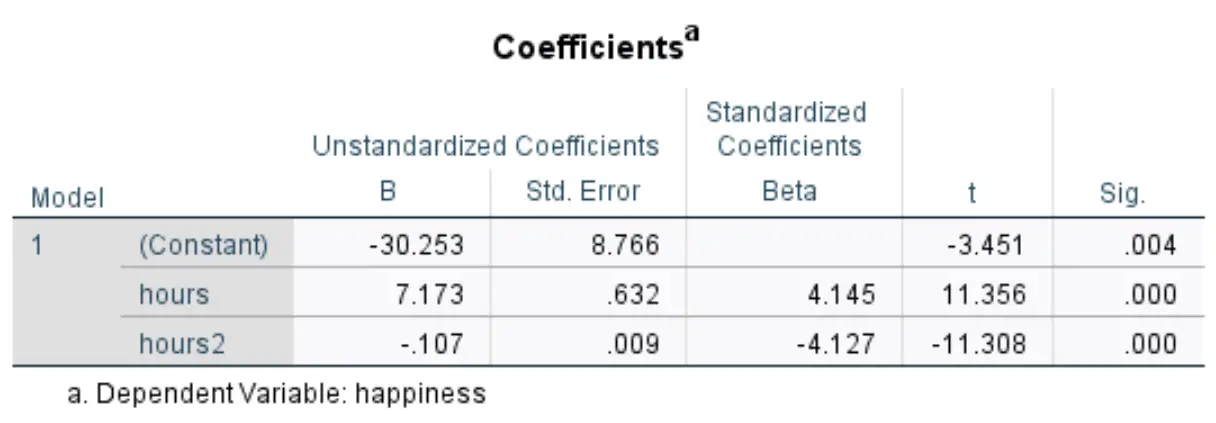
เราสามารถใช้ค่าในคอลัมน์ Unstandardized B เพื่อสร้างสมการการถดถอยโดยประมาณสำหรับชุดข้อมูลนี้ได้:

ระดับความสุขโดยประมาณ = -30.253 + 7.173*(ชั่วโมง) – 0.107*(ชั่วโมง ² )

เราสามารถใช้สมการนี้เพื่อค้นหาระดับความสุขโดยประมาณของแต่ละบุคคลโดยพิจารณาจากจำนวนชั่วโมงทำงานต่อสัปดาห์ เช่น คนที่ทำงาน 60 ชั่วโมงต่อสัปดาห์ควรมีระดับความสุขอยู่ที่ 14.97:

ระดับความสุขโดยประมาณ = -30.253 + 7.173*(60) – 0.107*(60 ² ) = 14.97

ในทางกลับกัน คนที่ทำงาน 30 ชั่วโมงต่อสัปดาห์ควรมีระดับความสุขอยู่ที่ 88.65

ระดับความสุขโดยประมาณ = -30.253 + 7.173*(30) – 0.107*(30 ² ) = 88.65

ขั้นตอนที่ 5: รายงานผลลัพธ์

สุดท้ายนี้ เราต้องการรายงานผลลัพธ์ของการถดถอยกำลังสองของเรา นี่คือตัวอย่างของวิธีการทำเช่นนี้:

การถดถอยกำลังสองดำเนินการเพื่อหาปริมาณความสัมพันธ์ระหว่างจำนวนชั่วโมงที่แต่ละคนทำงานและระดับความสุขที่สอดคล้องกัน (วัดจาก 0 ถึง 100) ใช้กลุ่มตัวอย่างจำนวน 16 คนในการวิเคราะห์

ผลการวิจัยพบว่ามีความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่างตัวแปรอธิบาย ชั่วโมง และ ชั่วโมงที่ ² กับ ความสุข ของตัวแปรตอบสนอง (F(2, 13) = 65.095, p < 0.000)

ตัวแปรอธิบายทั้งสองนี้รวมกันคิดเป็น 90.9% ของความแปรปรวนของความสุข

สมการถดถอยกลายเป็น:

ระดับความสุขโดยประมาณ = -30.253 + 7.173 (ชั่วโมง) – 0.107 ( ² ชั่วโมง)