วิธีดำเนินการถดถอยโลจิสติกใน spss

การถดถอยแบบลอจิสติก เป็นวิธีการที่เราใช้เพื่อให้พอดีกับ แบบจำลองการถดถอย เมื่อตัวแปรตอบสนองเป็นไบนารี

บทช่วยสอนนี้จะอธิบายวิธีการถดถอยโลจิสติกใน SPSS

ตัวอย่าง: การถดถอยโลจิสติกใน SPSS

ใช้ขั้นตอนต่อไปนี้เพื่อดำเนินการถดถอยโลจิสติกใน SPSS สำหรับชุดข้อมูลที่ระบุว่าผู้เล่นบาสเกตบอลระดับวิทยาลัยถูกร่างเข้าสู่ NBA หรือไม่ (ร่าง: 0 = ไม่, 1 = ใช่) โดยอิงตามเกรดเฉลี่ยของพวกเขา คะแนนต่อเกมและระดับดิวิชั่น

ขั้นตอนที่ 1: ป้อนข้อมูล

ขั้นแรก ให้ป้อนข้อมูลต่อไปนี้:

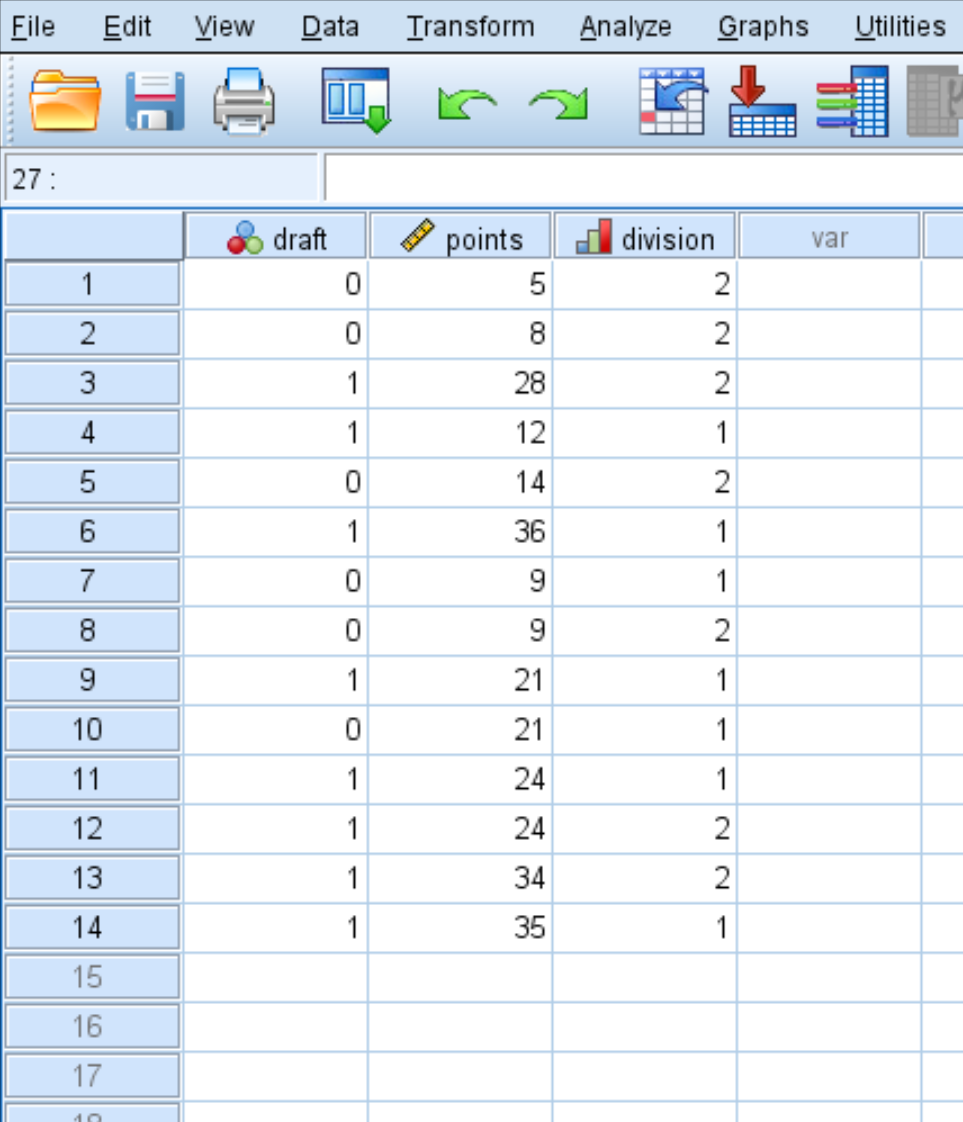
ขั้นตอนที่ 2: ดำเนินการถดถอยโลจิสติก

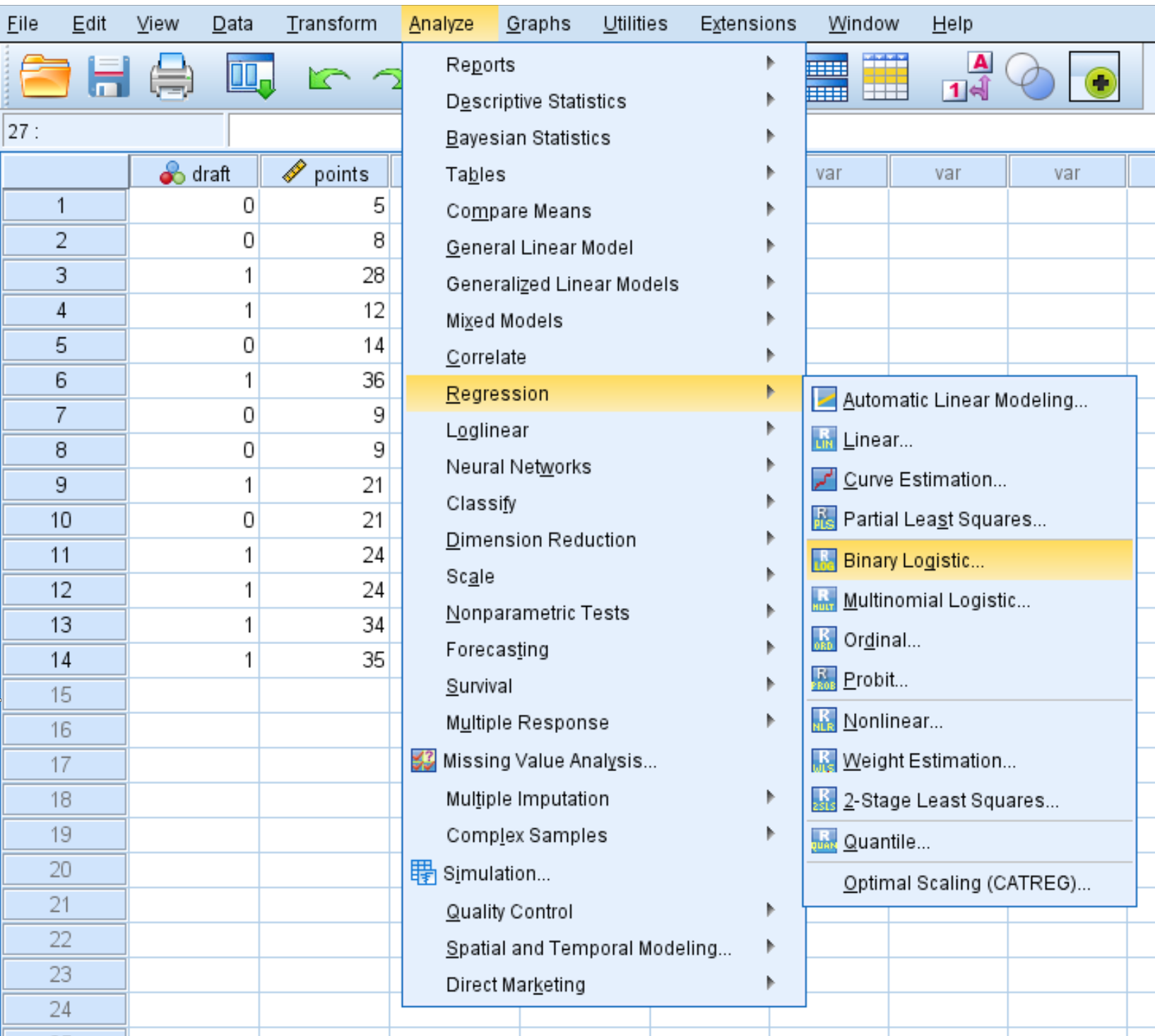
คลิกแท็บ วิเคราะห์ จากนั้นคลิก Regression จากนั้นคลิก Binary Logistic Regression :

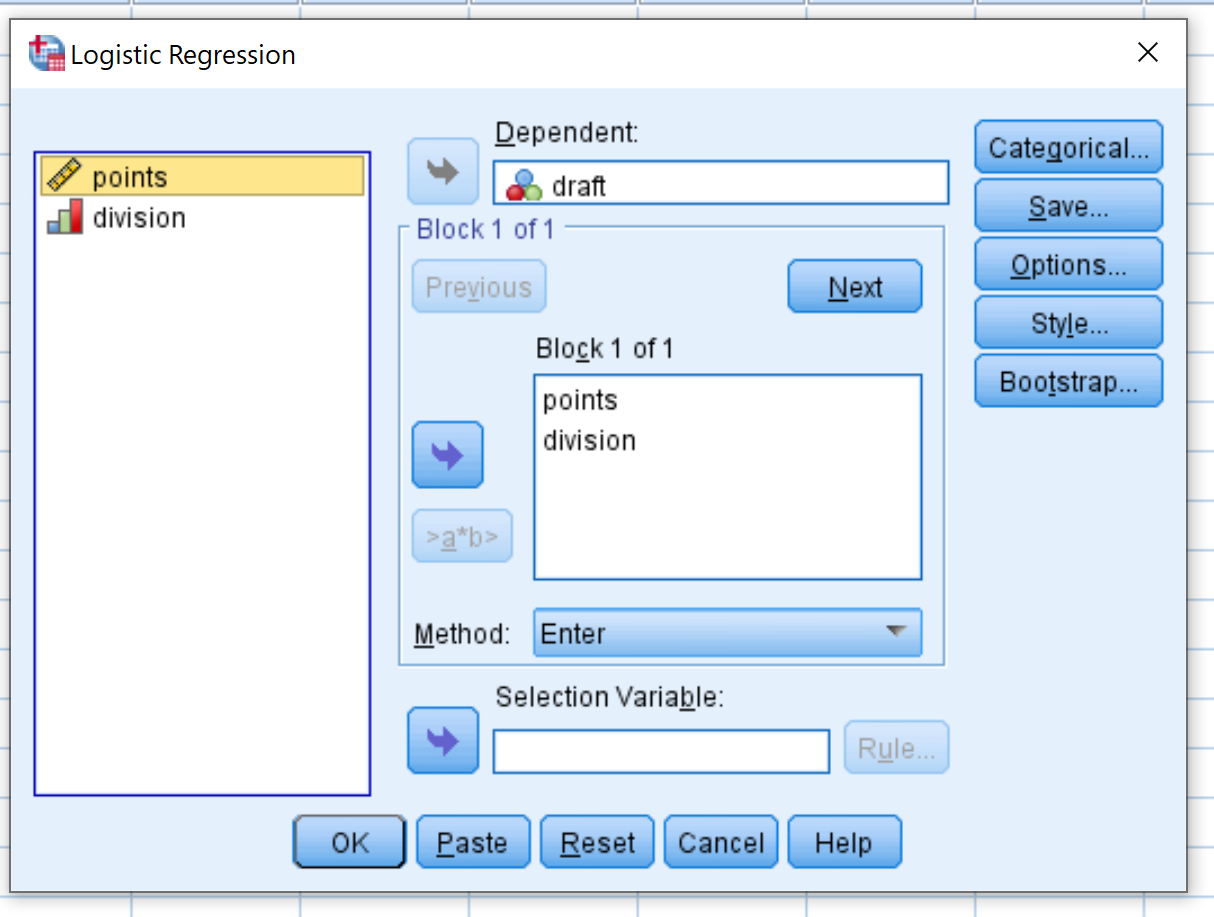
ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ลาก โปรเจ็กต์ ตัวแปรการตอบสนองแบบไบนารีลงในพื้นที่ที่มีป้ายกำกับว่าขึ้นอยู่กับ จากนั้นลากเครื่องหมาย โคลอน และ การหาร ตัวแปรทำนายลงในช่องที่มีข้อความว่า Block 1 จาก 1 ปล่อยให้ วิธี ตั้งค่าเป็น Enter จากนั้นคลิก ตกลง

ขั้นตอนที่ 3 ตีความผลลัพธ์

เมื่อคุณคลิก ตกลง ผลลัพธ์ของการถดถอยโลจิสติกจะปรากฏขึ้น:

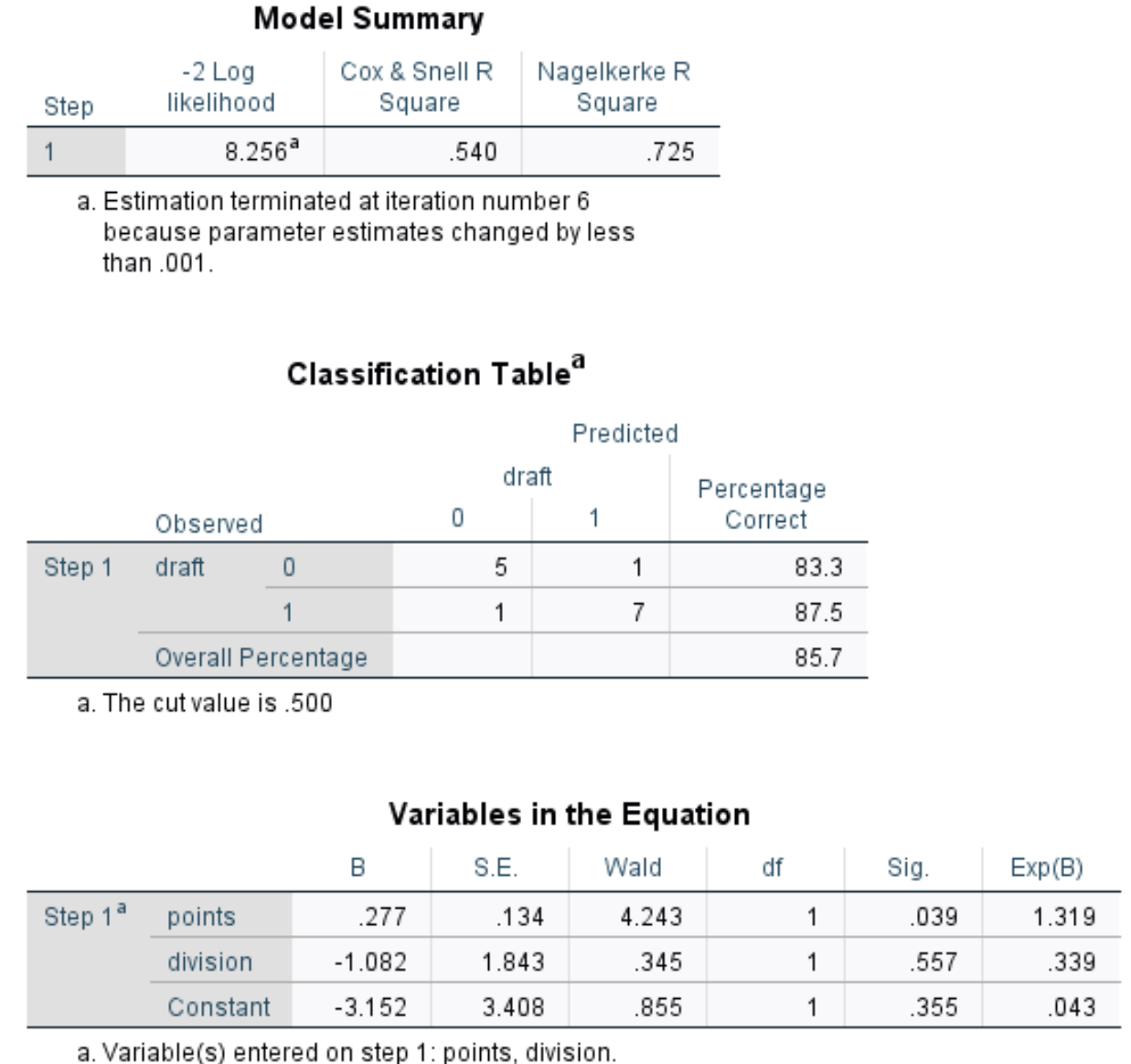
ต่อไปนี้เป็นวิธีการตีความผลลัพธ์:

สรุปโมเดล: หน่วยเมตริกที่มีประโยชน์ที่สุดในตารางนี้คือ Nagelkerke R Square ซึ่งบอกเราถึงเปอร์เซ็นต์ของการเปลี่ยนแปลงใน ตัวแปรตอบสนอง ที่สามารถอธิบายได้ด้วยตัวแปรทำนาย ในกรณีนี้ คะแนนและการหารสามารถอธิบายความแปรปรวนแบบร่างได้ 72.5%

ตารางการจำแนกประเภท: หน่วยวัดที่มีประโยชน์ที่สุดในตารางนี้คือเปอร์เซ็นต์โดยรวม ซึ่งบอกเราถึงเปอร์เซ็นต์ของการสังเกตที่แบบจำลองสามารถจัดประเภทได้อย่างถูกต้อง ในกรณีนี้ โมเดลการถดถอยโลจิสติกสามารถทำนายผลลัพธ์แบบร่างของผู้เล่น 85.7% ได้อย่างถูกต้อง

ตัวแปรในสมการ: ตารางสุดท้ายนี้ให้ค่าการวัดที่มีประโยชน์หลายประการ ได้แก่:

• Wald: สถิติการทดสอบ Wald สำหรับตัวแปรทำนายแต่ละตัว ซึ่งใช้เพื่อพิจารณาว่าตัวแปรทำนายแต่ละตัวมีนัยสำคัญทางสถิติหรือไม่
• Sig: ค่า p ซึ่งสอดคล้องกับสถิติการทดสอบ Wald สำหรับตัวแปรทำนายแต่ละตัว เราจะเห็นว่าค่า p ของ คะแนน คือ 0.039 และค่า p ของ การหาร คือ 0.557
• Exp(B): อัตราส่วนอัตราต่อรองสำหรับตัวแปรทำนายแต่ละตัว สิ่งนี้บอกเราถึงการเปลี่ยนแปลงของอัตราต่อรองของผู้เล่นที่ถูกร่างซึ่งเกี่ยวข้องกับการเพิ่มขึ้นหนึ่งหน่วยในตัวแปรทำนายที่กำหนด ตัวอย่างเช่น อัตราต่อรองของผู้เล่นดิวิชั่น 2 ที่ถูกดราฟท์เป็นเพียง 0.339 ของโอกาสของผู้เล่นดิวิชั่น 1 ที่ถูกดราฟท์ ในทำนองเดียวกัน การเพิ่มหน่วยคะแนนต่อเกมเพิ่มเติมแต่ละครั้งจะสัมพันธ์กับโอกาสที่เพิ่มขึ้น 1,319 ของผู้เล่นที่ถูกร่าง

จากนั้นเราสามารถใช้ค่าสัมประสิทธิ์ (ค่าในคอลัมน์ชื่อ B) เพื่อทำนายความน่าจะเป็นที่ผู้เล่นที่กำหนดจะถูกร่างโดยใช้สูตรต่อไปนี้:

ความน่าจะเป็น = e ^{-3.152 + 0.277 (คะแนน) – 1.082 (ส่วน)} / (1+e ^{-3.152 + 0.277 (คะแนน) – 1.082 (ส่วน)} )

ตัวอย่างเช่น ความน่าจะเป็นที่ผู้เล่นที่ได้เฉลี่ย 20 แต้มต่อเกมและเล่นในดิวิชั่น 1 จะถูกคำนวณดังนี้:

ความน่าจะเป็น = อี ^{-3.152 + 0.277(20) – 1.082(1)} / (1+e ^{-3.152 + 0.277(20) – 1.082(1)} ) = 0.787

เนื่องจากความน่าจะเป็นนี้มากกว่า 0.5 เราจึงคาดการณ์ว่าผู้เล่นรายนี้จะถูกดราฟต์

ขั้นตอนที่ 4 รายงานผล

สุดท้ายนี้ เราอยากจะรายงานผลลัพธ์ของการถดถอยลอจิสติกส์ของเรา นี่คือตัวอย่างของวิธีการทำเช่นนี้:

ดำเนินการถดถอยโลจิสติกเพื่อพิจารณาว่าคะแนนต่อเกมและระดับดิวิชั่นส่งผลต่อความน่าจะเป็นของผู้เล่นบาสเก็ตบอลอย่างไร ใช้ผู้เล่นทั้งหมด 14 คนในการวิเคราะห์

แบบจำลองอธิบายความแปรผันในผลลัพธ์ของโครงการได้ 72.5% และจำแนกกรณีได้ถูกต้อง 85.7%

โอกาสที่ผู้เล่นดิวิชั่น 2 จะถูกร่างเป็นเพียง 0.339 ของโอกาสที่ผู้เล่นดิวิชั่น 1 จะถูกร่าง

การเพิ่มหน่วยเพิ่มเติมแต่ละครั้งต่อเกมสัมพันธ์กับโอกาสที่เพิ่มขึ้น 1,319 ของผู้เล่นที่ถูกเกณฑ์ทหาร