คำแนะนำอย่างอ่อนโยนเกี่ยวกับผลรวมของกำลังสอง: sst, ssr, sse

การถดถอยเชิงเส้น ใช้เพื่อค้นหาเส้นที่ “พอดี” กับชุดข้อมูลมากที่สุด

เรามักจะใช้ ผลรวมของค่ากำลังสอง ที่แตกต่างกันสามค่าเพื่อวัดว่าเส้นการถดถอยเหมาะสมกับข้อมูลจริงเพียงใด:

1. ผลรวมของกำลังสองทั้งหมด (SST) – ผลรวมของกำลังสองของความแตกต่างระหว่างจุดข้อมูลแต่ละจุด (y _i ) และค่าเฉลี่ยของตัวแปรตอบสนอง ( y )

• SST = Σ(y _ผม – y ) ²

2. ผลรวมของการถดถอยกำลังสอง (SSR) – ผลรวมของกำลังสองของความแตกต่างระหว่างจุดข้อมูลที่คาดการณ์ (ŷ _i ) และค่าเฉลี่ยของตัวแปรตอบสนอง ( y )

• สสส = Σ(ŷ _ผม – y ) ²

3. ข้อผิดพลาดผลรวมกำลังสอง (SSE) – ผลรวมของกำลังสองของความแตกต่างระหว่างจุดข้อมูลที่คาดการณ์ (ŷ _i ) และจุดข้อมูลที่สังเกตได้ (y _i )

• SSE = Σ(ŷ _ผม – y _ผม ) ²

มีความสัมพันธ์ต่อไปนี้ระหว่างการวัดทั้งสามนี้:

SST = สสส + SSE

ถ้าเรารู้ค่าสองค่านี้ เราก็สามารถใช้พีชคณิตธรรมดาคำนวณค่าค่าที่สามได้

SSR, SST และ R-Square

R-squared บางครั้งเรียกว่าสัมประสิทธิ์การกำหนด เป็นการวัดว่าแบบจำลองการถดถอยเชิงเส้นเหมาะสมกับชุดข้อมูลได้ดีเพียงใด มันแสดงถึงสัดส่วนของความแปรปรวนใน ตัวแปรตอบสนอง ที่สามารถอธิบายได้ด้วยตัวแปรทำนาย

ค่า R-squared สามารถอยู่ในช่วงตั้งแต่ 0 ถึง 1 ค่า 0 บ่งชี้ว่าตัวแปรการตอบสนองไม่สามารถอธิบายได้ด้วยตัวแปรทำนายเลย ค่า 1 บ่งชี้ว่าตัวแปรตัวทำนายสามารถอธิบายตัวแปรตอบสนองได้อย่างสมบูรณ์แบบโดยไม่มีข้อผิดพลาด

เมื่อใช้ SSR และ SST เราสามารถคำนวณ R กำลังสองได้ดังนี้:

R กำลังสอง = SSR / SST

ตัวอย่างเช่น หาก SSR สำหรับแบบจำลองการถดถอยที่กำหนดคือ 137.5 และ SST คือ 156 เราจะคำนวณ R กำลังสองดังนี้:

R กำลังสอง = 137.5 / 156 = 0.8814

สิ่งนี้บอกเราว่า 88.14% ของความแปรผันในตัวแปรตอบสนองสามารถอธิบายได้ด้วยตัวแปรทำนาย

คำนวณ SST, SSR, SSE: ตัวอย่างทีละขั้นตอน

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งแสดงจำนวนชั่วโมงที่นักเรียน 6 คนเรียนพร้อมคะแนนสอบปลายภาค:

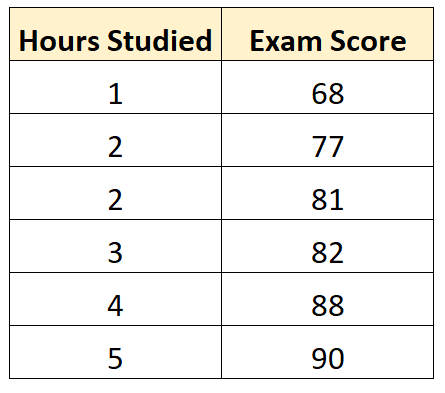
การใช้ซอฟต์แวร์ทางสถิติบางตัว (เช่น R , Excel , Python ) หรือแม้แต่ด้วยมือ เราจะเห็นว่าบรรทัดที่เหมาะสมที่สุดคือ:

คะแนน = 66.615 + 5.0769*(ชั่วโมง)

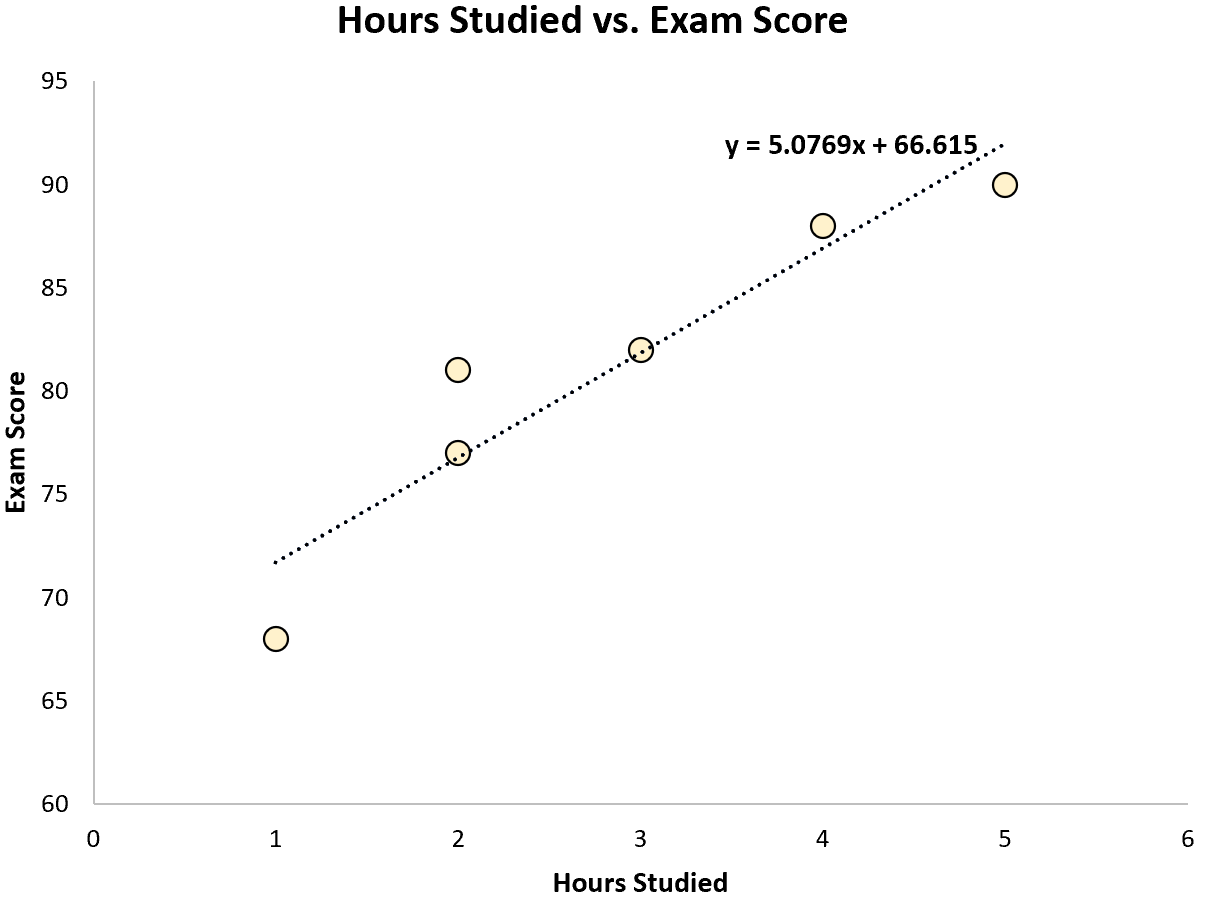
เมื่อเราทราบเส้นสมการที่เหมาะที่สุดแล้ว เราสามารถใช้ขั้นตอนต่อไปนี้เพื่อคำนวณ SST, SSR และ SSE:

ขั้นตอนที่ 1: คำนวณค่าเฉลี่ยของตัวแปรตอบสนอง

ค่าเฉลี่ยของตัวแปรตอบสนอง ( y ) กลายเป็น 81

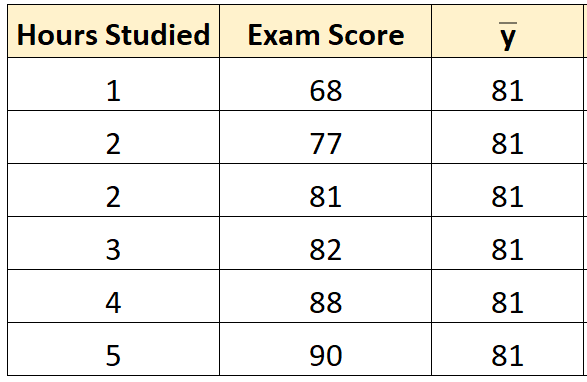
ขั้นตอนที่ 2: คำนวณค่าที่คาดการณ์ไว้สำหรับการสังเกตแต่ละครั้ง

จากนั้นเราสามารถใช้เส้นสมการที่เหมาะสมที่สุดเพื่อคำนวณคะแนนสอบที่คาดการณ์ไว้ () สำหรับนักเรียนแต่ละคน

ตัวอย่างเช่น คะแนนสอบที่คาดการณ์ไว้สำหรับนักเรียนที่เรียนหนึ่งชั่วโมงคือ:

คะแนน = 66.615 + 5.0769*(1) = 71.69

เราสามารถใช้แนวทางเดียวกันนี้เพื่อค้นหาคะแนนที่คาดการณ์ไว้สำหรับนักเรียนแต่ละคน:

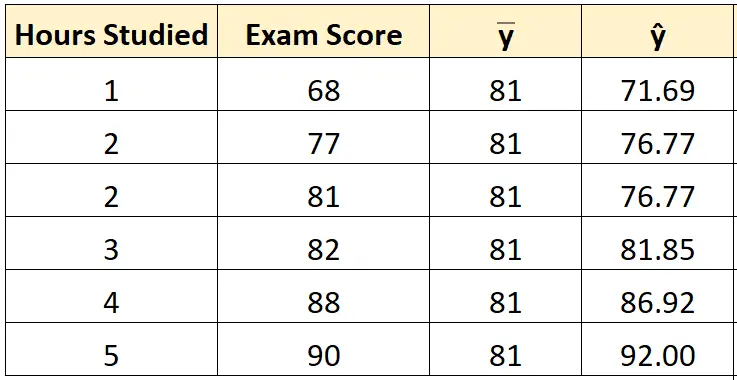
ขั้นตอนที่ 3: คำนวณผลรวมของกำลังสอง (SST)

จากนั้นเราก็สามารถคำนวณผลรวมของกำลังสองทั้งหมดได้

ตัวอย่างเช่น ผลรวมของกำลังสองสำหรับนักเรียนคนแรกคือ:

(y _ผม – y ) ² = (68 – 81) ² = 169 .

เราสามารถใช้แนวทางเดียวกันในการหาผลรวมของกำลังสองสำหรับนักเรียนแต่ละคน:

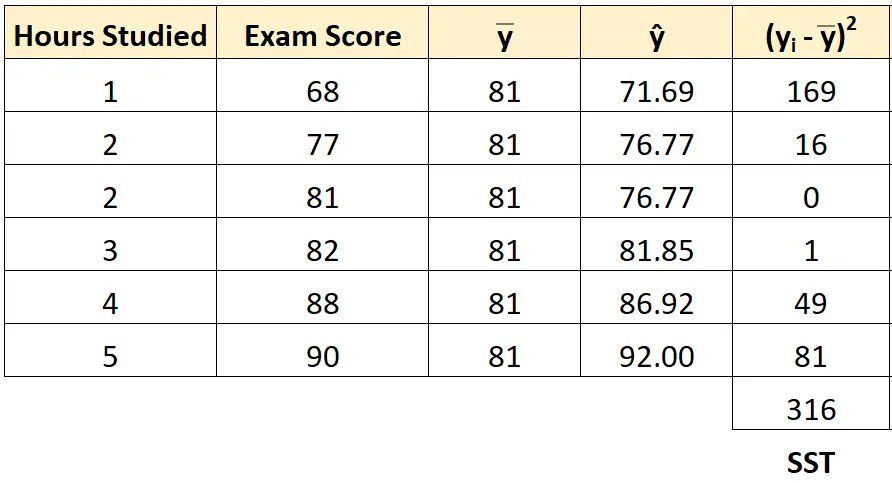
ผลรวมของกำลังสองกลายเป็น 316 .

ขั้นตอนที่ 4: คำนวณผลรวมของการถดถอยกำลังสอง (SSR)

จากนั้นเราก็สามารถคำนวณผลรวมของการถดถอยกำลังสองได้

ตัวอย่างเช่น ผลรวมของการถดถอยกำลังสองสำหรับนักเรียนคนแรกคือ:

( _ŷi – y ) ² = (71.69 – 81) ² = 86.64 .

เราสามารถใช้แนวทางเดียวกันนี้เพื่อค้นหาการถดถอยของผลรวมกำลังสองของนักเรียนแต่ละคน:

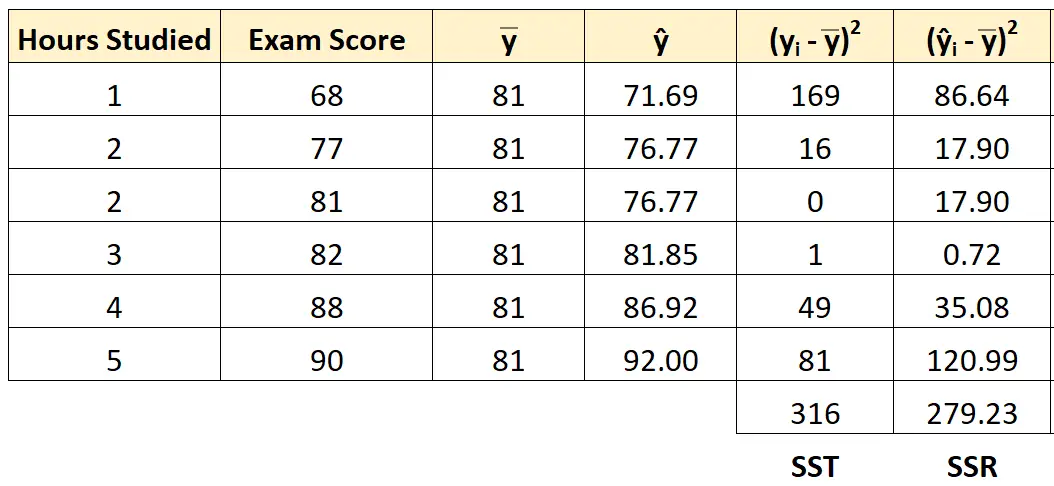
ผลรวมของการถดถอยกำลังสองกลายเป็น 279.23

ขั้นตอนที่ 5: คำนวณผลรวมของข้อผิดพลาดกำลังสอง (SSE)

จากนั้นเราก็สามารถคำนวณความคลาดเคลื่อนของผลรวมของกำลังสองได้

ตัวอย่างเช่น ผลรวมของค่าคลาดเคลื่อนกำลังสองสำหรับนักเรียนคนแรกคือ:

(ŷ _ผม – y _ผม ) ² = (71.69 – 68) ² = 13.63 .

เราสามารถใช้แนวทางเดียวกันนี้เพื่อค้นหาผลรวมของค่าคลาดเคลื่อนกำลังสองของนักเรียนแต่ละคน:

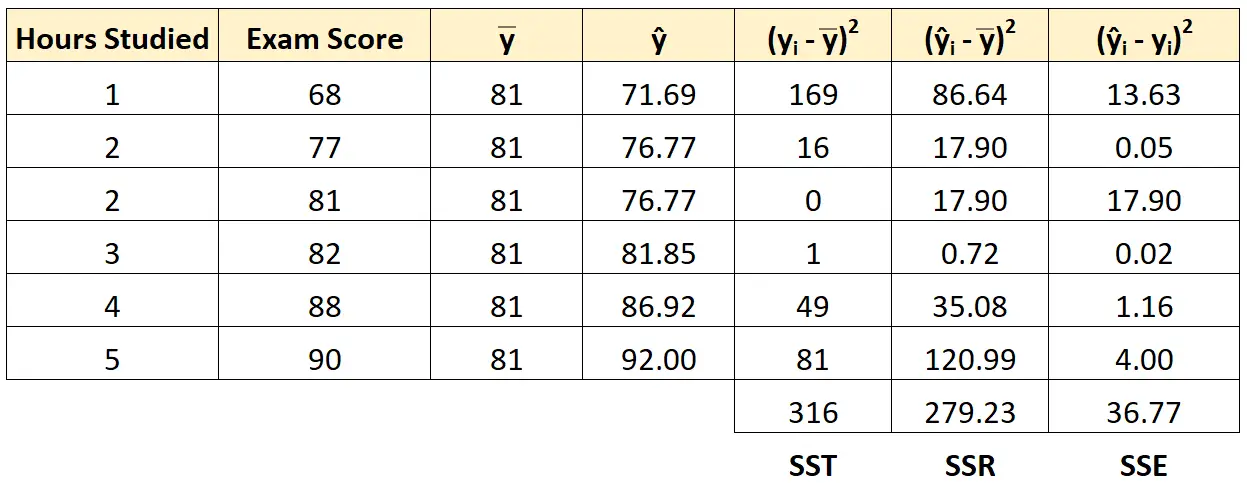
เราสามารถตรวจสอบได้ว่า SST = SSR + SSE

• SST = สสส + SSE
• 316 = 279.23 + 36.77

นอกจากนี้เรายังสามารถคำนวณ R กำลังสองของแบบจำลองการถดถอยได้โดยใช้สมการต่อไปนี้:

• R กำลังสอง = SSR / SST
• R กำลังสอง = 279.23 / 316
• R กำลังสอง = 0.8836

ข้อมูลนี้บอกเราว่า 88.36% ของความแปรผันของคะแนนสอบสามารถอธิบายได้ด้วยจำนวนชั่วโมงที่เรียน

แหล่งข้อมูลเพิ่มเติม

คุณสามารถใช้เครื่องคำนวณต่อไปนี้เพื่อคำนวณ SST, SSR และ SSE โดยอัตโนมัติสำหรับเส้นการถดถอยเชิงเส้นแบบธรรมดา:

เครื่องคิดเลข SST
เครื่องคิดเลข RSS
เครื่องคิดเลข ESS