Stdev.p กับ stdev.s ใน excel: อะไรคือความแตกต่าง?

มีฟังก์ชันที่แตกต่างกันสามฟังก์ชันที่คุณสามารถใช้เพื่อคำนวณค่าเบี่ยงเบนมาตรฐานใน Excel:

1. STDEV.P: ฟังก์ชันนี้จะคำนวณค่าเบี่ยงเบนมาตรฐานของประชากร ใช้ฟังก์ชันนี้เมื่อช่วงของค่าแสดงถึงประชากรทั้งหมด

ฟังก์ชันนี้ใช้สูตรต่อไปนี้:

ค่าเบี่ยงเบนมาตรฐานของประชากร = √Σ (x _i – μ) ² / N

ทอง:

• Σ: สัญลักษณ์กรีกหมายถึง “ผลรวม”
• x _i : ค่า ^{ที่ i} ของชุดข้อมูล
• μ: ค่าเฉลี่ยของประชากร
• N: จำนวนการสังเกตทั้งหมด

2. STDEV.S: ฟังก์ชันนี้จะคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง ใช้ฟังก์ชันนี้เมื่อช่วงของค่าแสดงถึงตัวอย่างค่าแทนที่จะเป็นประชากรทั้งหมด

ฟังก์ชันนี้ใช้สูตรต่อไปนี้:

ค่าเบี่ยงเบนมาตรฐานตัวอย่าง = √Σ (x _i – x ) ² / (n-1)

ทอง:

• Σ: สัญลักษณ์กรีกหมายถึง “ผลรวม”
• x _i : ค่า ^{ที่ i} ของชุดข้อมูล
• x : หมายถึงตัวอย่าง
• N: จำนวนการสังเกตทั้งหมด

3. STDEV: ฟังก์ชันนี้ยังคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างด้วย โดยจะส่งกลับค่าเดียวกันกับฟังก์ชัน STDEV.S ทุก ประการ

หมายเหตุทางเทคนิค:

เนื่องจากสูตรค่าเบี่ยงเบนมาตรฐานของประชากรหารด้วย N แทนที่จะเป็น n-1 ค่าเบี่ยงเบนมาตรฐานของประชากรจะน้อยกว่าค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างเสมอ

สาเหตุที่ค่าเบี่ยงเบนมาตรฐานของประชากรมีค่าน้อยลง เพราะถ้าเรารู้ค่าประชากรแต่ละค่า เราจะรู้ค่าเบี่ยงเบนมาตรฐานที่แน่นอน

อย่างไรก็ตาม เมื่อเรามีเพียงตัวอย่างประชากร เราก็มีความไม่แน่นอนมากขึ้นเกี่ยวกับค่าเบี่ยงเบนมาตรฐานที่แน่นอนของประชากรโดยรวม ดังนั้นค่าประมาณของค่าเบี่ยงเบนมาตรฐานจึงต้องมากกว่านั้น

ตัวอย่างต่อไปนี้แสดงวิธีการใช้ฟังก์ชันเหล่านี้ในทางปฏิบัติ

ตัวอย่าง: STDEV.P กับ STDEV.S ใน Excel

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ใน Excel:

ภาพหน้าจอต่อไปนี้แสดงวิธีคำนวณค่าเบี่ยงเบนมาตรฐานของชุดข้อมูลโดยใช้สูตรค่าเบี่ยงเบนมาตรฐานที่แตกต่างกัน 3 สูตร:

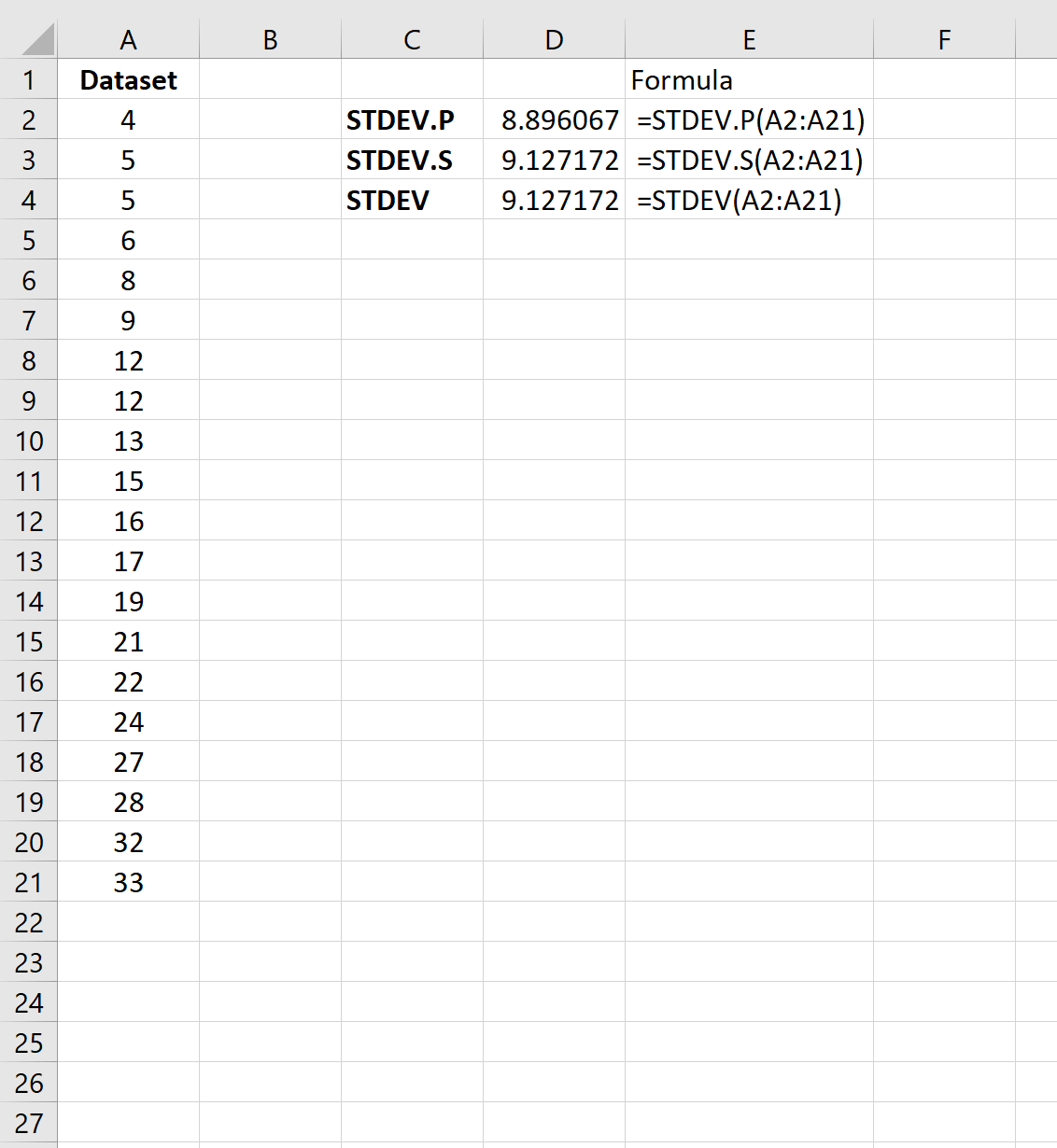
ค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างกลายเป็น 9.127 และค่าเบี่ยงเบนมาตรฐานของประชากรกลายเป็น 8.896

ตามที่กล่าวไว้ข้างต้น ค่าเบี่ยงเบนมาตรฐานของประชากรจะน้อยกว่าค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างเสมอ

เมื่อใดควรใช้ STDEV.P กับ STDEV.S

ในกรณีส่วนใหญ่ เราไม่สามารถรวบรวมข้อมูลสำหรับประชากรทั้งหมดได้ ดังนั้นเราจึงรวบรวมข้อมูลเฉพาะกลุ่ม ตัวอย่าง เท่านั้น

ดังนั้นเราจึงใช้ STDEV.S ในการคำนวณค่าเบี่ยงเบนมาตรฐานของชุดข้อมูลเกือบทุกครั้ง เนื่องจากโดยทั่วไปชุดข้อมูลของเราจะแสดงถึงตัวอย่าง

โปรดทราบว่า STDEV และ STDEV.S ส่งคืนค่าเดียวกันทุกประการ ดังนั้นเราจึงสามารถใช้ฟังก์ชันใดฟังก์ชันหนึ่งเพื่อคำนวณค่าเบี่ยงเบนมาตรฐานตัวอย่างของชุดข้อมูลที่กำหนดได้