วิธีทำการทดสอบ tukey-kramer post hoc ใน excel
การวิเคราะห์ความแปรปรวนแบบทางเดียว ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่
สมมติฐาน ที่ใช้ในการวิเคราะห์ความแปรปรวนมีดังนี้:
สมมติฐานว่าง (H 0 ): µ 1 = µ 2 = µ 3 = … = µ k (ค่าเฉลี่ยของแต่ละกลุ่มเท่ากัน)
สมมติฐานทางเลือก: (ฮา): อย่างน้อยก็มีวิธีการหนึ่งที่แตกต่างจากวิธีอื่นๆ
ถ้า ค่า p ของ ANOVA ต่ำกว่าระดับนัยสำคัญ เราสามารถปฏิเสธสมมติฐานว่างได้และสรุปได้ว่าเรามีหลักฐานเพียงพอที่จะบอกว่าค่าเฉลี่ยของกลุ่มอย่างน้อยหนึ่งรายการแตกต่างจากค่าเฉลี่ยอื่นๆ
อย่างไรก็ตาม นี่ไม่ได้บอกเราว่ากลุ่ม ใด มีความแตกต่างกัน นี่บอกเราว่าค่าเฉลี่ยกลุ่มไม่เท่ากันทั้งหมด หากต้องการทราบว่ากลุ่มใดมีความแตกต่างกัน เราต้องทำการทดสอบหลังการทดสอบ
การทดสอบหลังการทดสอบที่ใช้กันมากที่สุดคือ การทดสอบ Tukey-Kramer ซึ่งเปรียบเทียบค่าเฉลี่ยระหว่างแต่ละกลุ่มที่รวมกันเป็นคู่
ตัวอย่างต่อไปนี้แสดงวิธีดำเนินการทดสอบ Tukey-Kramer ใน Excel
ตัวอย่าง: การทดสอบ Tukey-Kramer ใน Excel
สมมติว่าเราทำการวิเคราะห์ความแปรปรวนแบบทางเดียวในสามกลุ่ม: A, B และ C ผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียวจะแสดงอยู่ด้านล่าง:
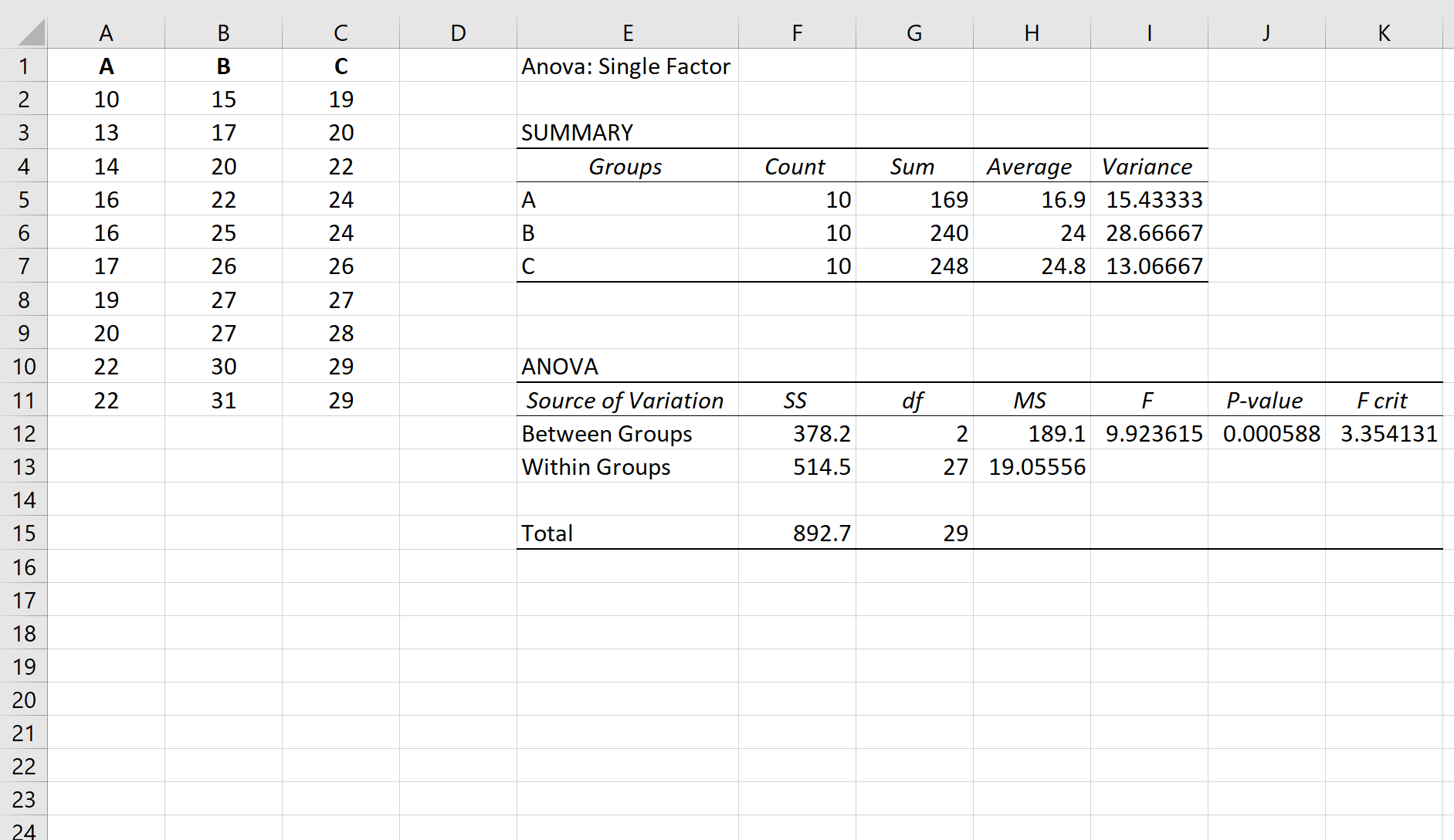
ที่เกี่ยวข้อง: วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel
ค่า p ของตาราง ANOVA คือ 0.000588 เนื่องจากค่า p นี้น้อยกว่า 0.05 เราจึงสามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่าค่าเฉลี่ยระหว่างทั้งสามกลุ่ม ไม่ เท่ากัน
หากต้องการทราบว่าค่าเฉลี่ยของกลุ่ม ใด ที่แตกต่างกัน เราสามารถทำการทดสอบหลังการทดสอบของ Tukey-Kramer ได้โดยใช้ขั้นตอนต่อไปนี้:
ขั้นตอนที่ 1: ค้นหาผลต่างค่าเฉลี่ยสัมบูรณ์ระหว่างแต่ละกลุ่ม
ขั้นแรก เราจะค้นหาความแตกต่างเฉลี่ยสัมบูรณ์ระหว่างแต่ละกลุ่มโดยใช้วิธีการที่ระบุไว้ในตารางแรกของผลลัพธ์ ANOVA:
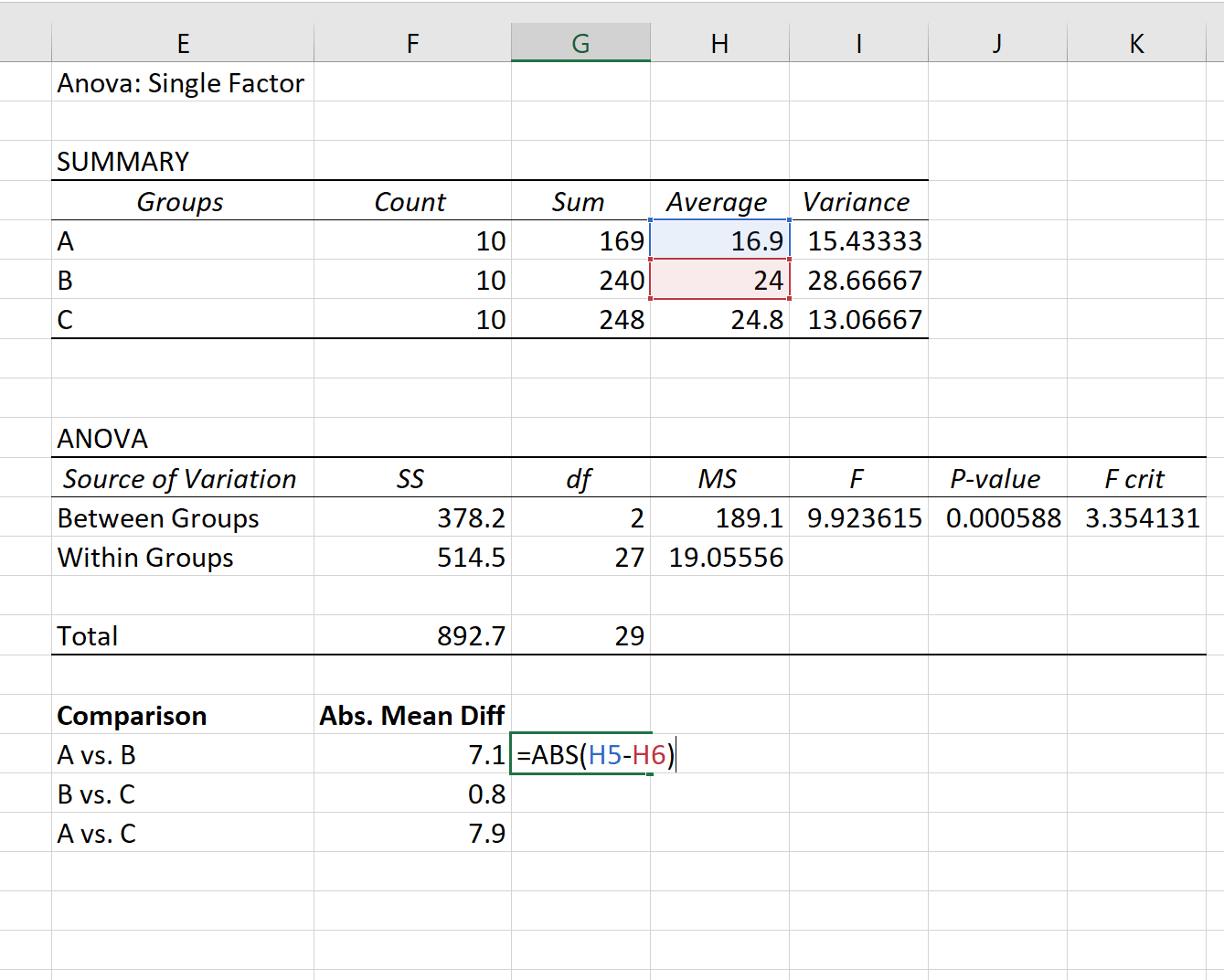
ขั้นตอนที่ 2: ค้นหาค่าวิกฤตของ Q
ต่อไป เราจำเป็นต้องค้นหาค่าวิกฤตของ Q โดยใช้สูตรต่อไปนี้:
ค่าวิกฤต Q = Q*√(s 2 กลุ่ม / n.)
ทอง:
- Q = ค่าช่วงของตารางนักเรียน Q
- s 2 รวมกัน = ความแปรปรวนรวมกันในทุกกลุ่ม
- ไม่. = ขนาดตัวอย่างสำหรับกลุ่มที่กำหนด
หากต้องการค้นหาค่า Q คุณสามารถอ้างอิงถึงตาราง Studentized range Q ซึ่งมีลักษณะดังนี้:
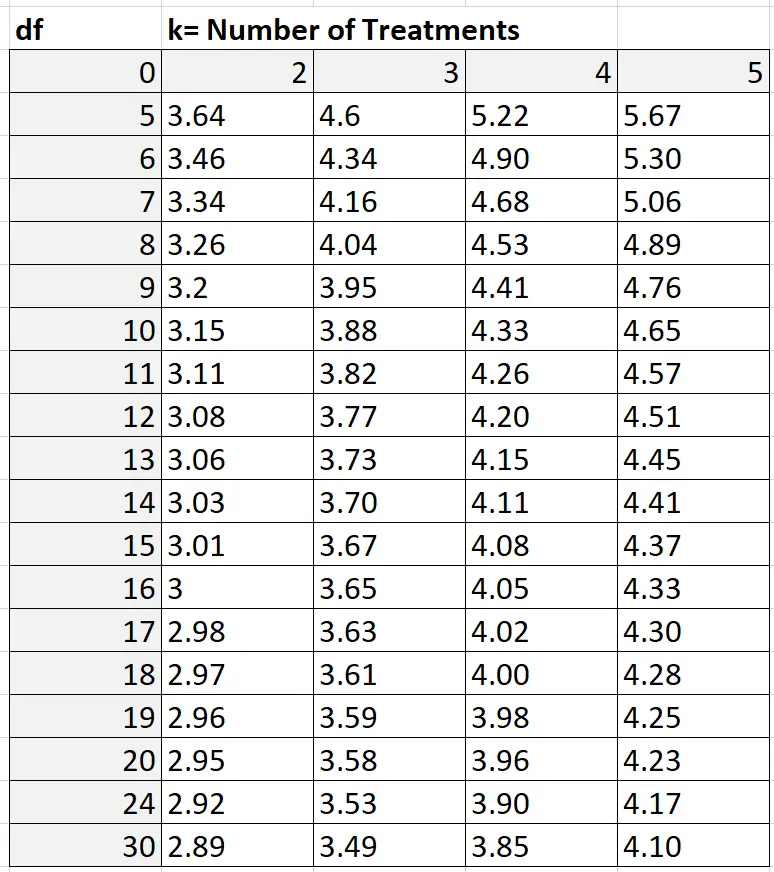
ในตัวอย่างของเรา k = จำนวนกลุ่ม เช่น k = 3 องศาความอิสระคำนวณได้ดังนี้: nk = 30 – 3 = 27 เนื่องจาก 27 ไม่ได้แสดงในตารางด้านบน เราจึงใช้ค่าประมาณแบบอนุรักษ์นิยมที่ 24 . จากค่า k = 3 และ df = 24 เราพบว่า Q = 3.53
ความแปรปรวนรวมกลุ่มสามารถคำนวณได้เป็นค่าเฉลี่ยของความแปรปรวนของกลุ่ม ซึ่งกลายเป็น 19.056
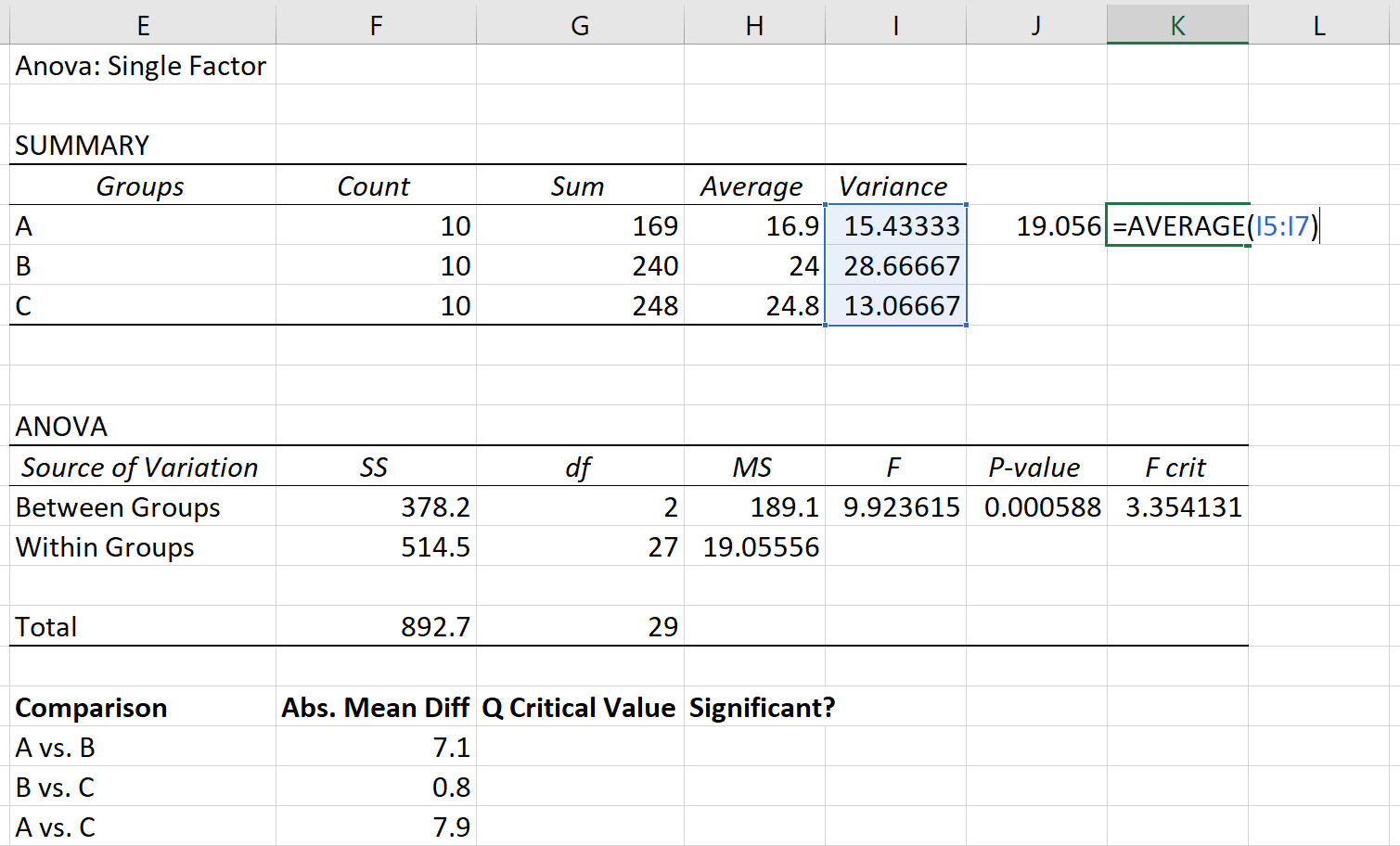
สุดท้ายขนาดกลุ่มตัวอย่างของแต่ละกลุ่มคือ 10
ดังนั้นค่าวิกฤต Q ของเราสามารถคำนวณได้ดังนี้:
ค่าวิกฤต Q = Q*√(s 2 กลุ่ม / n.) = 3.53*√(19.056/10) = 4.87
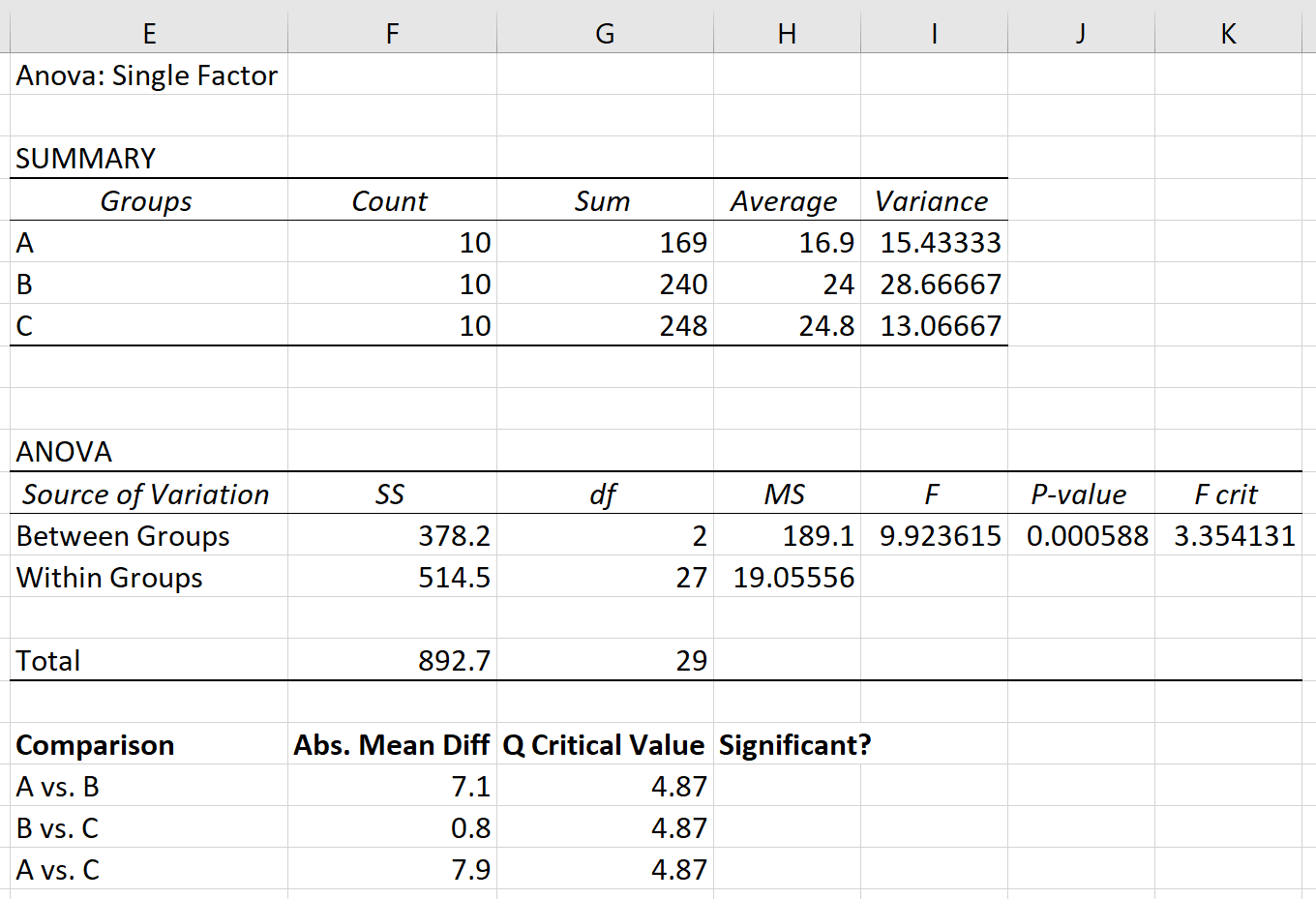
ขั้นตอนที่ 3: พิจารณาว่าค่าเฉลี่ยของกลุ่มใดแตกต่างกัน
สุดท้ายนี้ เราสามารถเปรียบเทียบความแตกต่างเฉลี่ยสัมบูรณ์ระหว่างแต่ละกลุ่มกับค่าวิกฤต Q ได้ หากความแตกต่างเฉลี่ยสัมบูรณ์มากกว่าค่าวิกฤติ Q ความแตกต่างระหว่างค่าเฉลี่ยกลุ่มจะมีนัยสำคัญทางสถิติ:
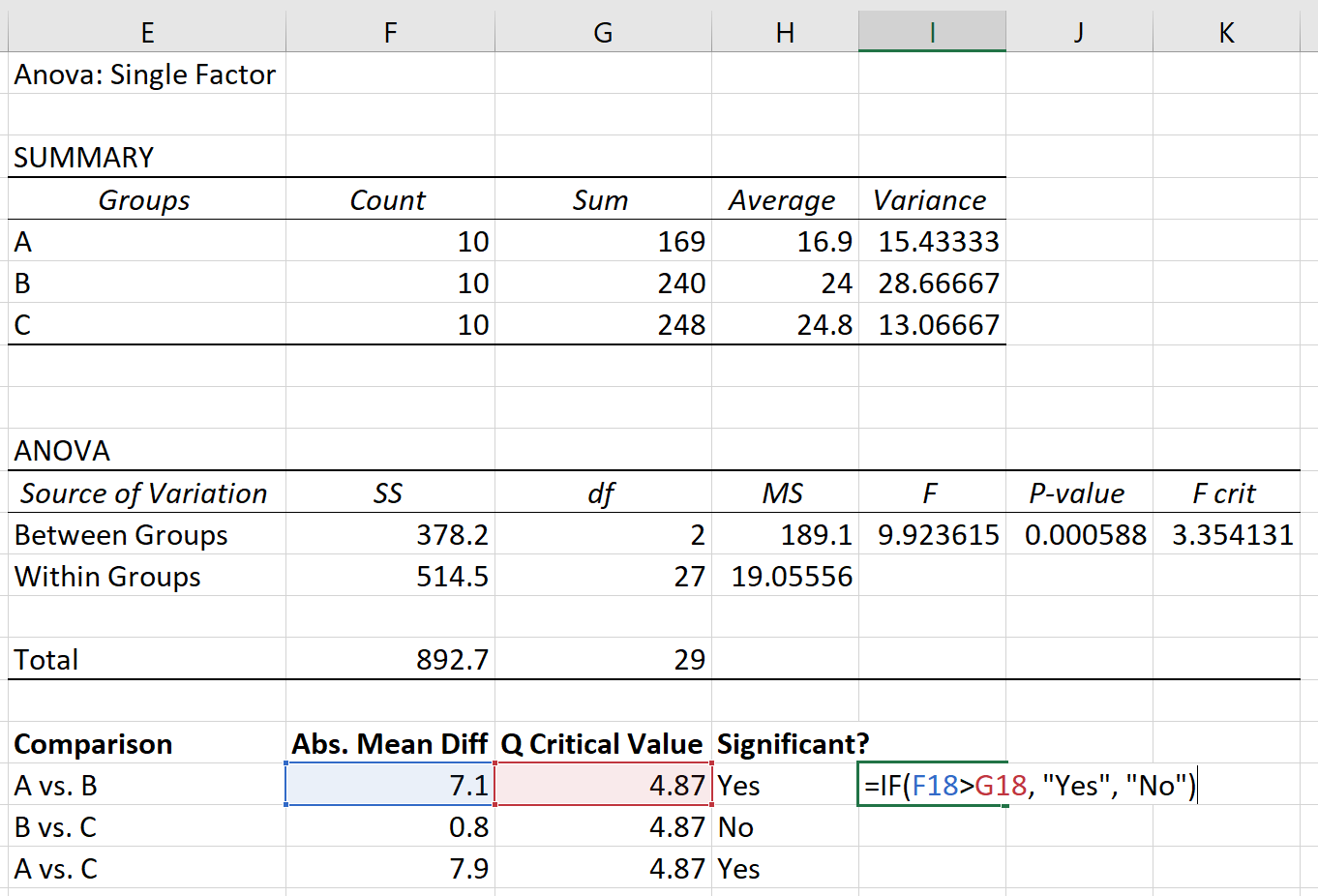
จากการทดสอบหลังการทดสอบของ Tukey-Kramer เราพบสิ่งต่อไปนี้:
- ความแตกต่างในค่าเฉลี่ยระหว่างกลุ่ม A และกลุ่ม B มีนัยสำคัญทางสถิติ
- ความแตกต่างในค่าเฉลี่ยระหว่างกลุ่ม B และกลุ่ม C ไม่มี นัยสำคัญทางสถิติ
- ความแตกต่างในค่าเฉลี่ยระหว่างกลุ่ม A และกลุ่ม C มีนัยสำคัญทางสถิติ
แหล่งข้อมูลเพิ่มเติม
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel
คู่มือการใช้การทดสอบหลังการทดลองด้วย ANOVA