วิธีค้นหาค่าวิกฤต z บนเครื่องคิดเลข ti-84

ทุกครั้งที่คุณทำการทดสอบสมมติฐาน คุณจะได้รับสถิติการทดสอบ หากต้องการทราบว่าผลการทดสอบสมมติฐานมีนัยสำคัญทางสถิติหรือไม่ คุณสามารถเปรียบเทียบสถิติการทดสอบกับ ค่า Z ที่สำคัญได้ หากค่าสัมบูรณ์ของสถิติการทดสอบมากกว่าค่า Z วิกฤต ผลการทดสอบจะมีนัยสำคัญทางสถิติ

หากต้องการค้นหาค่าวิกฤต Z บนเครื่องคิดเลข TI-84 คุณสามารถใช้ฟังก์ชันต่อไปนี้:

invNorm(ความน่าจะเป็น, μ, σ)

ทอง:

• ความน่าจะเป็น: ระดับนัยสำคัญ
• μ: ค่าเฉลี่ยประชากร
• σ: ส่วนเบี่ยงเบนมาตรฐานประชากร

คุณสามารถเข้าถึงฟังก์ชันนี้บนเครื่องคิดเลข TI-84 ได้โดยกด 2 จากนั้นกด vars สิ่งนี้จะนำคุณไปยังหน้าจอ DISTR ซึ่งคุณสามารถใช้ invNorm() :

บทช่วยสอนนี้จะแชร์ตัวอย่างต่างๆ ของการใช้ฟังก์ชัน invNorm() เพื่อค้นหาค่า Z ที่สำคัญบนเครื่องคิดเลข TI-84

ตัวอย่างที่ 1: ค่าวิกฤติ Z สำหรับการทดสอบทางด้านซ้าย

คำถาม: ค้นหาค่า Z วิกฤตสำหรับการทดสอบด้านซ้ายที่มีระดับนัยสำคัญเท่ากับ 0.05

คำตอบ: invNorm(.05, 0, 1) = -1.6449

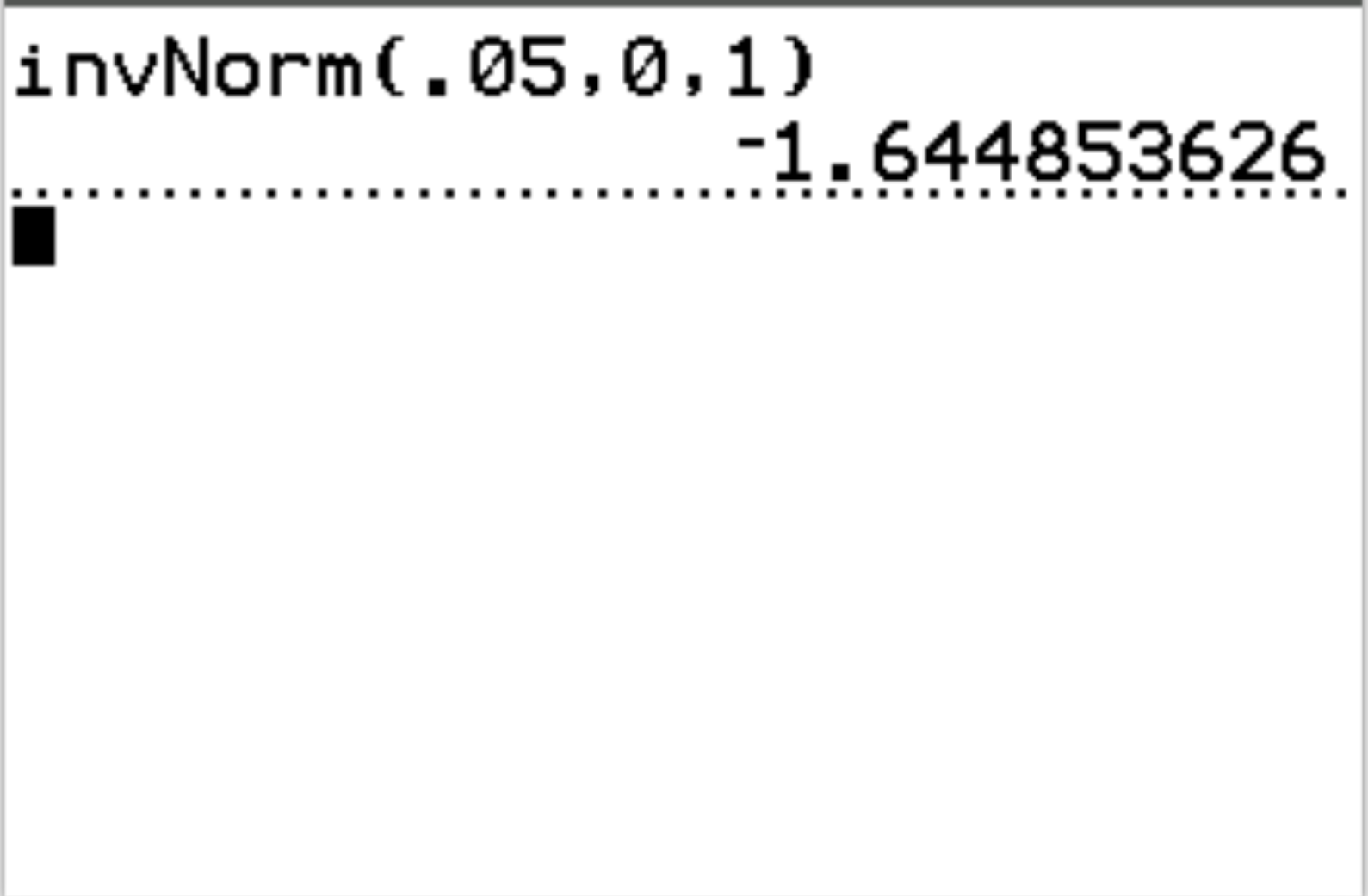
การตีความ: หากสถิติการทดสอบน้อยกว่า -1.6449 ผลการทดสอบจะมีนัยสำคัญทางสถิติที่ α = 0.05

ตัวอย่างที่ 2: ค่าวิกฤต Z สำหรับการทดสอบหางตรง

คำถาม: ค้นหาค่า Z วิกฤตสำหรับการทดสอบด้านข้างที่ถูกต้องโดยมีระดับนัยสำคัญเท่ากับ 0.10

คำตอบ: invT(1-.10, 0, 1) = 1.2816

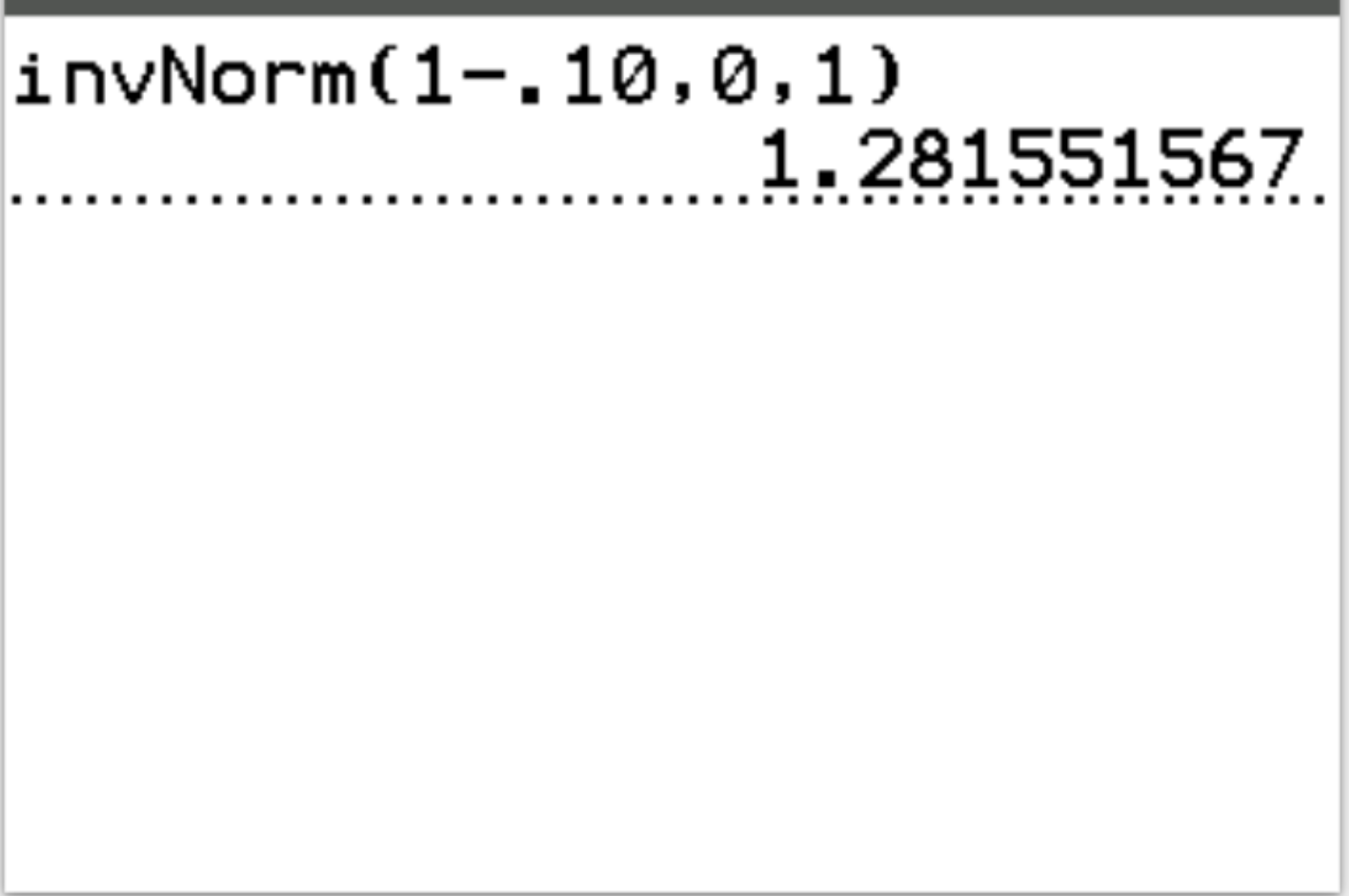
การตีความ: หากสถิติการทดสอบมากกว่า 1.2816 ผลการทดสอบจะมีนัยสำคัญทางสถิติที่ α = 0.10

ตัวอย่างที่ 3: ค่า Z วิกฤตสำหรับการทดสอบสองด้าน

คำถาม: ค้นหาค่า Z วิกฤตสำหรับการทดสอบแบบสองด้านที่มีระดับนัยสำคัญเท่ากับ 0.05

คำตอบ: invNorm(.05/2, 0, 1) = -1.96, 1.96

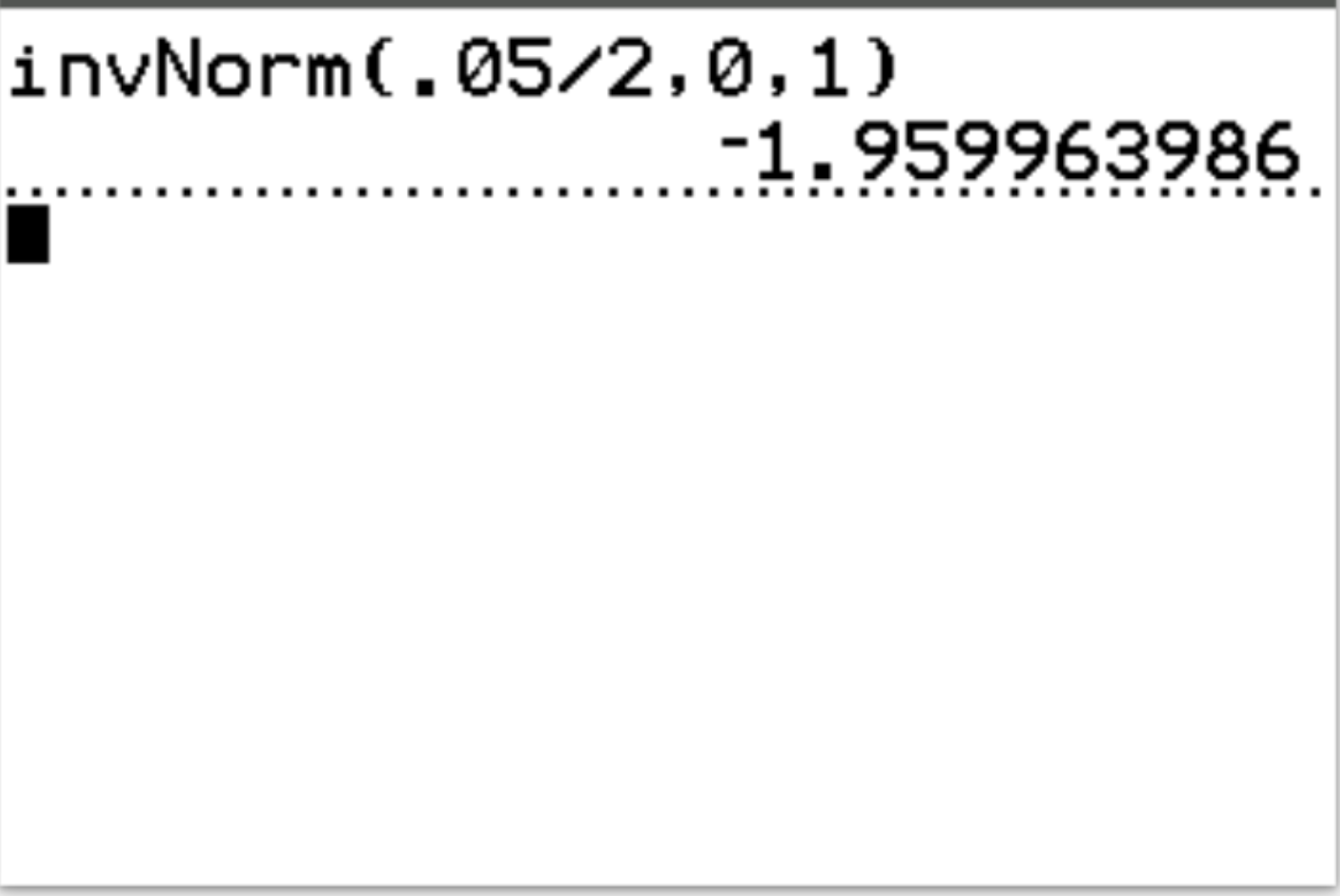
การตีความ: เนื่องจากนี่เป็นการทดสอบแบบสองด้าน เราจึงมีค่าวิกฤตสองค่า: -1.96 และ 1.96 หากสถิติการทดสอบน้อยกว่า -1.96 หรือมากกว่า 1.96 ผลการทดสอบจะมีนัยสำคัญทางสถิติที่ α = 0.05