วิธีการสร้างกราฟผลลัพธ์ anova ใน excel

การวิเคราะห์ความแปรปรวนแบบทางเดียว ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่

เมื่อตีความผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียว การสร้างกราฟเพื่อแสดงภาพความแตกต่างระหว่างค่าเฉลี่ยของกลุ่มอาจเป็นประโยชน์

ตัวอย่างต่อไปนี้แสดงวิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวและสร้างกราฟผลลัพธ์ใน Excel

ตัวอย่าง: วิธีการสร้างกราฟผลลัพธ์ ANOVA ใน Excel

สมมติว่าศาสตราจารย์ สุ่มขอให้ นักเรียน 30 คนในชั้นเรียนใช้วิธีเรียนแบบใดแบบหนึ่งจากสามวิธีเพื่อเตรียมตัวสอบ

ภาพหน้าจอต่อไปนี้แสดงคะแนนของนักเรียนตามวิธีที่พวกเขาใช้:

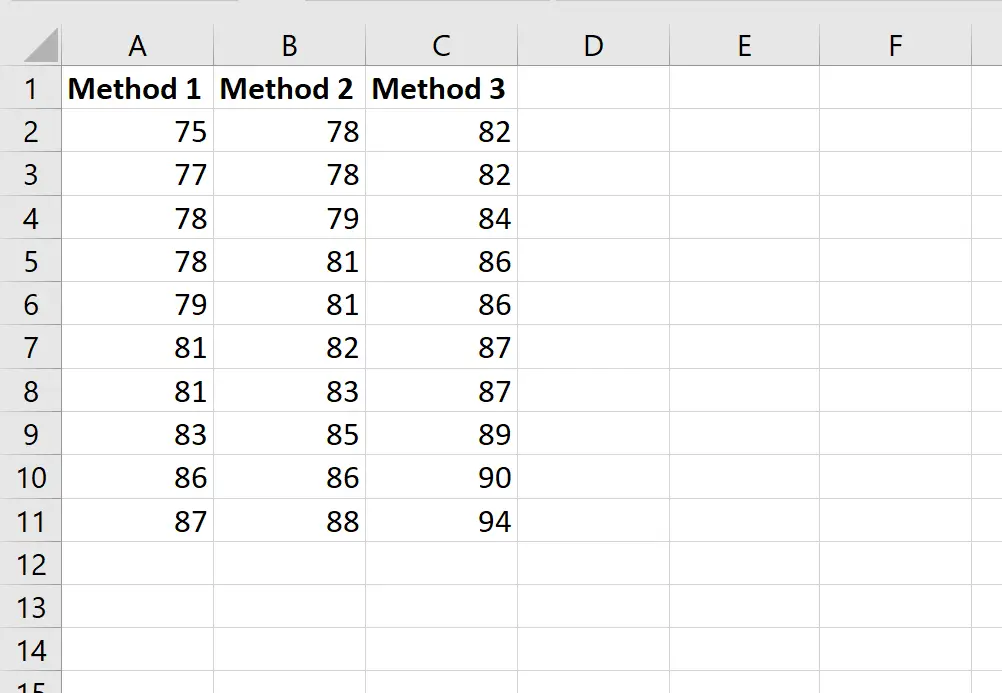
สมมติว่าศาสตราจารย์ต้องการทำการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อพิจารณาว่าคะแนนเฉลี่ยของทั้ง 3 กลุ่มเท่ากันหรือไม่

เมื่อต้องการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel ให้คลิกแท็บ ข้อมูล บน Ribbon ด้านบน จากนั้นคลิก การวิเคราะห์ข้อมูล ในกลุ่ม วิเคราะห์

หากคุณไม่เห็นตัวเลือก การวิเคราะห์ข้อมูล คุณ ต้อง โหลดซอฟต์แวร์ Analysis ToolPak ฟรีก่อน

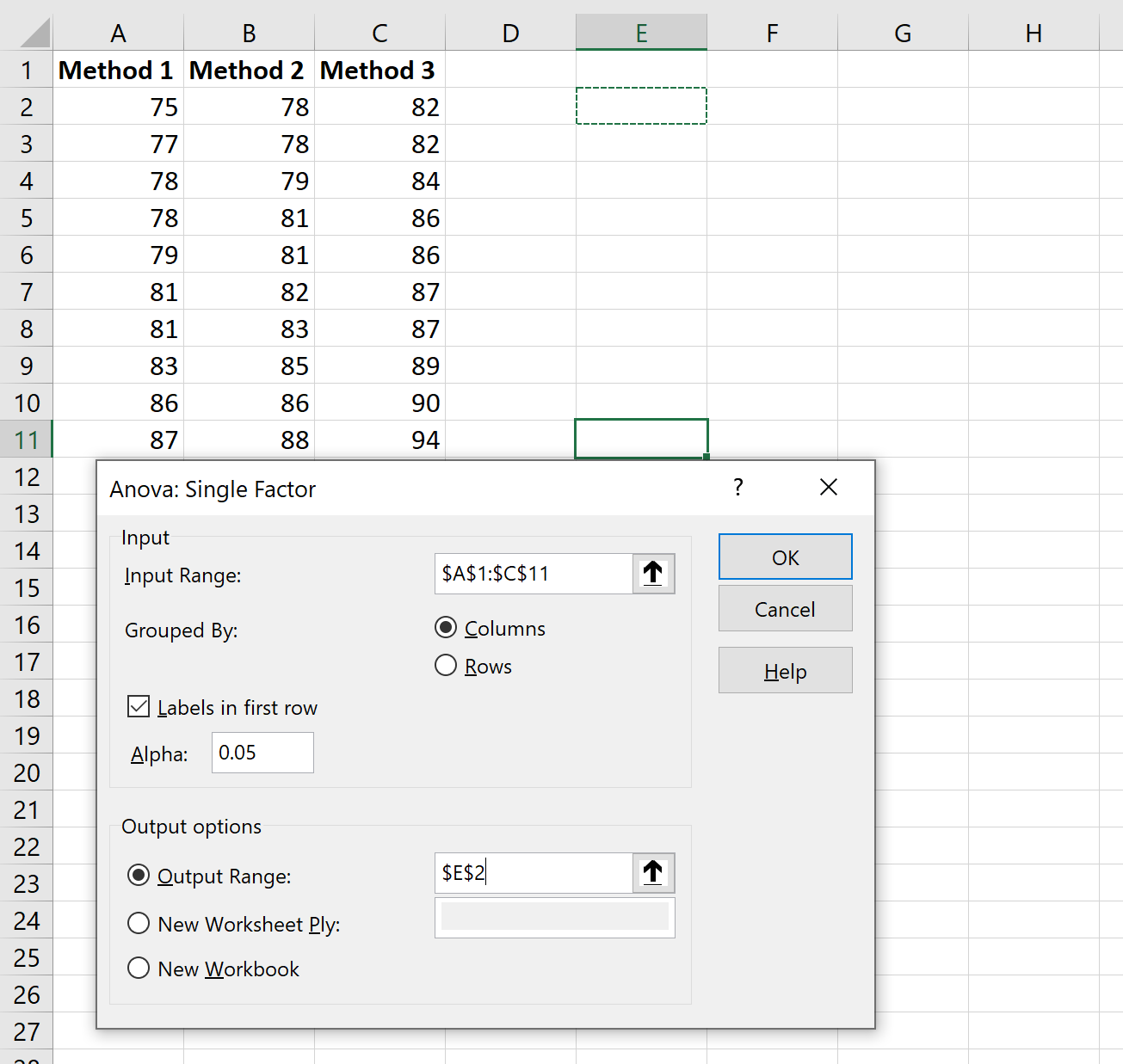
ในแผงใหม่ที่ปรากฏขึ้น คลิก Anova: Single Factor จากนั้นคลิก ตกลง

ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ป้อนข้อมูลต่อไปนี้:

เมื่อคุณคลิก ตกลง ผลลัพธ์ ANOVA แบบทางเดียวจะปรากฏขึ้น:

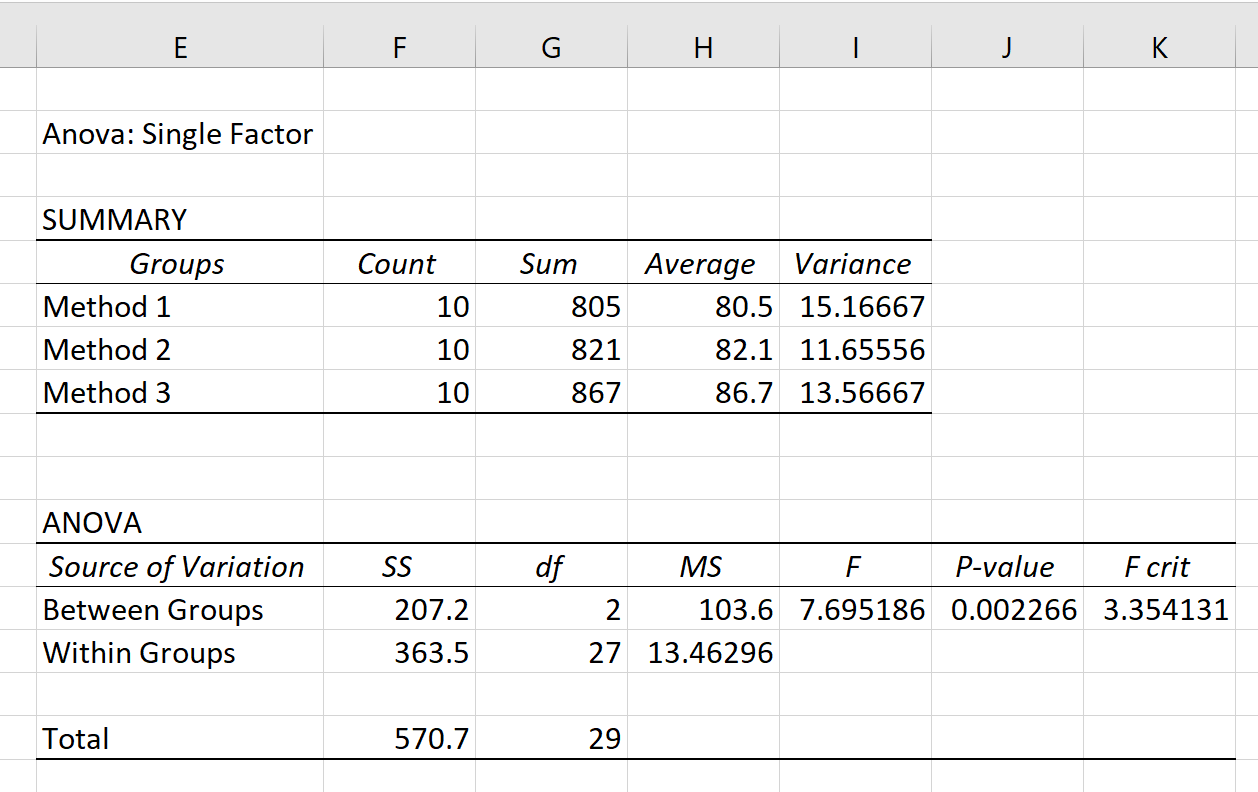
ค่าที่ใหญ่ที่สุดในเอาต์พุตคือ p-value ซึ่งกลายเป็น 0.002266

โปรดจำไว้ว่าการวิเคราะห์ความแปรปรวนทางเดียวใช้สมมติฐานว่างและทางเลือกต่อไปนี้:

• H ₀ : ค่าเฉลี่ยกลุ่มทั้งหมดเท่ากัน
• _HA : ค่าเฉลี่ยของกลุ่มไม่เท่ากันทั้งหมด

เนื่องจากค่า p น้อยกว่า α = 0.05 เราจึงปฏิเสธสมมติฐานว่างและสรุปว่าค่าเฉลี่ยกลุ่มทั้งหมดไม่เท่ากัน

ซึ่งหมายความว่าวิธีการศึกษาทั้งสามวิธีไม่ได้ทำให้คะแนนสอบเฉลี่ยเท่ากัน

เพื่อให้เห็นภาพผลลัพธ์ ANOVA เหล่านี้ เราสามารถสร้าง boxplots ที่จัดกลุ่มซึ่งแสดงการกระจายของผลการสอบสำหรับวิธีการศึกษาแต่ละวิธี

เมื่อต้องการทำเช่นนี้ ให้ไฮไลต์ช่วงเซลล์ A2:C11 จากนั้นคลิกแท็บ แทรก ที่ริบบิ้นด้านบน จากนั้นคลิกไอคอน กล่องและหนวด ในกลุ่ม แผนภูมิ :

ตารางต่อไปนี้จะปรากฏขึ้น:

อย่าลังเลที่จะเปลี่ยนช่วงแกน Y และเพิ่มคำอธิบายเพื่อทำให้แผนภูมินี้อ่านง่ายขึ้น:

Boxplots แต่ละกล่องจะแสดงการกระจายผลการทดสอบสำหรับวิธีการศึกษาแต่ละวิธี

เส้นที่อยู่ตรงกลางของแต่ละ Boxplot แสดงถึงคะแนนสอบเฉลี่ยสำหรับวิธีการศึกษาแต่ละวิธี และ “x” ตัวเล็กหมายถึงคะแนนสอบโดยเฉลี่ย

โดยไม่ต้องดูผลลัพธ์ของตาราง ANOVA เราจะเห็นว่าคะแนนสอบเฉลี่ยสำหรับวิธีการศึกษาที่ 3 นั้นสูงกว่าวิธีการศึกษาอีกสองวิธีอย่างมีนัยสำคัญ

เรายังเห็นได้ด้วยว่าเหตุใดค่า p ในตาราง ANOVA จึงมีนัยสำคัญทางสถิติ กล่าวคือ วิธีการศึกษาทั้งสามวิธีไม่มีค่าเฉลี่ยเท่ากันอย่างชัดเจน

ด้วยการสร้าง Boxplot ทั้งสามนี้ เราจะสามารถเข้าใจผลลัพธ์ของ One-Way ANOVA ได้ดีขึ้น

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการทั่วไปอื่นๆ ใน Excel:

วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน Excel
วิธีการดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางใน Excel
วิธีการดำเนินการวัด ANOVA ซ้ำใน Excel
วิธีทำการทดสอบ Tukey-Kramer Post Hoc ใน Excel