ความรู้เบื้องต้นเกี่ยวกับการกระจายปัวซอง
การแจกแจงปัวซง เป็นหนึ่งในการแจกแจงที่ได้รับความนิยมมากที่สุดในสถิติ
เพื่อให้เข้าใจถึงการกระจายตัวของปัวซอง จะเป็นประโยชน์อย่างยิ่งที่จะทำความเข้าใจการทดลองของปัวซองก่อน
การทดลองปลา
การทดลองปัวซอง คือการทดลองที่มีคุณสมบัติดังต่อไปนี้:
- สามารถนับจำนวนความสำเร็จของการทดสอบได้
- จำนวนความสำเร็จโดยเฉลี่ยที่เกิดขึ้นในช่วงเวลา (หรือช่องว่าง) ที่ระบุเป็นที่ทราบ
- แต่ละผลลัพธ์มีความเป็นอิสระ
- ความน่าจะเป็นของความสำเร็จที่เกิดขึ้นนั้นแปรผันตามขนาดของช่วงเวลา
ตัวอย่างของการทดลองปัวซองคือจำนวนการเกิดต่อชั่วโมงในโรงพยาบาลที่กำหนด ตัวอย่างเช่น สมมติว่าโรงพยาบาลแห่งใดแห่งหนึ่งมีการคลอดบุตรโดยเฉลี่ย 10 คนต่อชั่วโมง นี่คือการทดลองแบบปัวซอง เนื่องจากมีคุณสมบัติสี่ประการต่อไปนี้:
- สามารถนับจำนวนความสำเร็จของการทดลองได้ – เราสามารถนับจำนวนการเกิดได้
- จำนวนการเกิดโดยเฉลี่ยที่เกิดขึ้นในช่วงเวลาหนึ่งเป็นที่รู้ – เป็นที่รู้กันว่ามีการเกิดโดยเฉลี่ย 10 ครั้งต่อชั่วโมง
- แต่ละผลลัพธ์มีความเป็นอิสระ – ความน่าจะเป็นที่แม่คนหนึ่งจะคลอดบุตรในเวลาที่กำหนดนั้นไม่ขึ้นอยู่กับความน่าจะเป็นที่มารดาอีกคนจะคลอดบุตร
- ความน่าจะเป็นของความสำเร็จที่เกิดขึ้นนั้นแปรผันตามขนาดของช่วงเวลา ยิ่งช่วงเวลานานเท่าไร ความน่าจะเป็นในการเกิดก็จะยิ่งสูงขึ้นเท่านั้น
เราสามารถใช้การแจกแจงแบบปัวซองเพื่อตอบคำถามเกี่ยวกับความน่าจะเป็นเกี่ยวกับการทดลองแบบปัวซอง เช่น:
- ความน่าจะเป็นที่จะเกิดมากกว่า 12 คนในชั่วโมงที่กำหนดคือข้อใด
- ความน่าจะเป็นที่จะเกิดน้อยกว่า 5 คนในชั่วโมงที่กำหนดคือข้อใด
- ความน่าจะเป็นที่การเกิดระหว่าง 8 ถึง 11 จะเกิดขึ้นในช่วงเวลาที่กำหนดเป็นเท่าใด
การกระจายพันธุ์ปลา
การแจกแจงแบบปัวซอง อธิบายถึงความน่าจะเป็นที่จะประสบความสำเร็จ k รายการในช่วงเวลาที่กำหนด
หาก ตัวแปรสุ่ม X ตามหลังการแจกแจงแบบปัวซอง ความน่าจะเป็นที่ความสำเร็จของ X = k สามารถหาได้จากสูตรต่อไปนี้:
P(X=k) = แลม บ์ * อี – แล / k!
ทอง:
- แล: จำนวนความสำเร็จโดยเฉลี่ยที่เกิดขึ้นในช่วงเวลาที่กำหนด
- k: จำนวนความสำเร็จ
- e: ค่าคงที่เท่ากับประมาณ 2.71828
ตัวอย่างเช่น สมมติว่าโรงพยาบาลแห่งใดแห่งหนึ่งมีการคลอดบุตรโดยเฉลี่ย 2 คนต่อชั่วโมง เราสามารถใช้สูตรด้านบนเพื่อกำหนดความน่าจะเป็นที่จะเกิด 0, 1, 2, 3 ครั้ง เป็นต้น ในชั่วโมงที่กำหนด:
P(X=0) = 2 0 * อี – 2 / 0! = 0.1353
P(X=1) = 2 1 * อี – 2 / 1! = 0.2707
P(X=2) = 2 2 * อี – 2 / 2! = 0.2707
P(X=3) = 2 3 * อี – 2 / 3! = 0.1805
เราสามารถคำนวณความน่าจะเป็นของการเกิดจำนวนเท่าใดก็ได้จนถึงอนันต์ จากนั้นเราจะสร้างฮิสโตแกรมอย่างง่ายเพื่อแสดงภาพการแจกแจงความน่าจะเป็น:

การคำนวณความน่าจะเป็นปัวซองสะสม
การคำนวณความน่าจะเป็นแบบปัวซองเดียวเป็นเรื่องง่าย (เช่น ความน่าจะเป็นที่โรงพยาบาลมีการคลอดบุตร 3 ครั้งในชั่วโมงที่กำหนด) โดยใช้สูตรด้านบน แต่ในการคำนวณความน่าจะเป็นแบบปัวซองสะสม เราจำเป็นต้องเพิ่มความน่าจะเป็นส่วนบุคคล
ตัวอย่างเช่น สมมติว่าเราต้องการทราบความน่าจะเป็นที่โรงพยาบาลจะมีการคลอดบุตร 1 ครั้งหรือน้อยกว่านั้นในชั่วโมงที่กำหนด เราจะใช้สูตรต่อไปนี้เพื่อคำนวณความน่าจะเป็นนี้:
P(X≤1) = P(X=0) + P(X=1) = 0.1353 + 0.2707 = 0.406
สิ่งนี้เรียก ว่าความน่าจะเป็นสะสม เนื่องจากเกี่ยวข้องกับการบวกความน่าจะเป็นหลายรายการ เราสามารถคำนวณความน่าจะเป็นสะสมที่จะเกิด k หรือน้อยกว่าในชั่วโมงที่กำหนดได้โดยใช้สูตรที่คล้ายกัน:
P(X≤0) = P(X=0) = 0.1353
P(X≤1) = P(X=0) + P(X=1) = 0.1353 + 0.2707 = 0.406
P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0.1353 + 0.2707 + 0.2707 = 0.6767
เราสามารถคำนวณความน่าจะเป็นสะสมเหล่านี้สำหรับจำนวนการเกิดเท่าใดก็ได้จนถึงอนันต์ จากนั้นเราสามารถสร้างฮิสโตแกรมเพื่อแสดงภาพการแจกแจงความน่าจะเป็นสะสมได้:
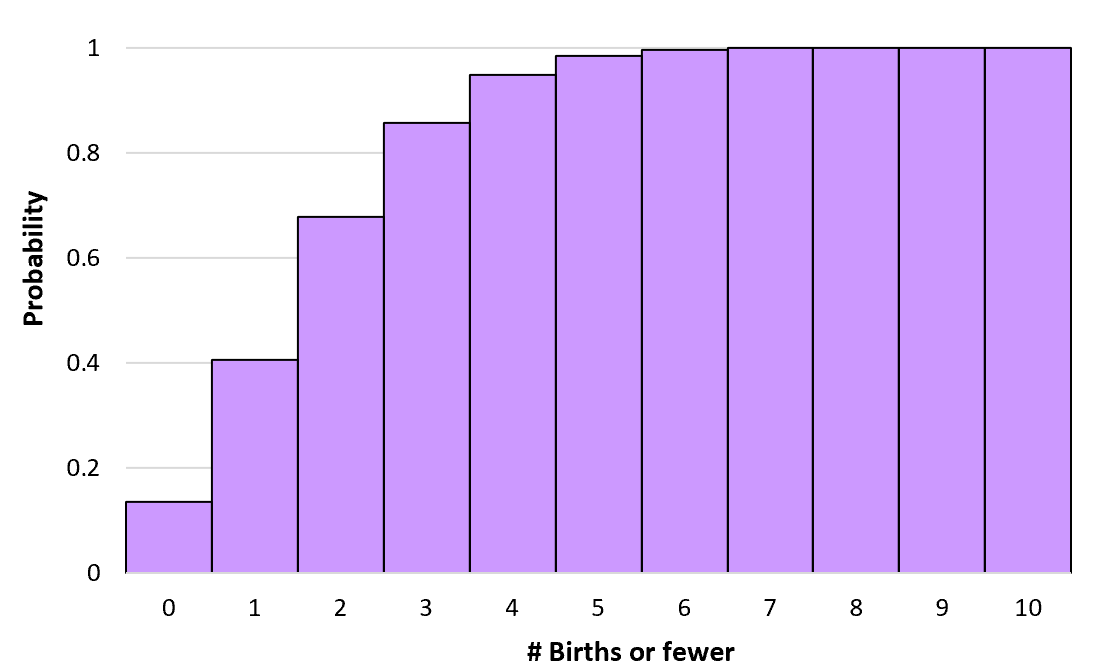
คุณสมบัติของการแจกแจงแบบปัวซอง
การแจกแจงปัวซองมีคุณสมบัติดังต่อไปนี้:
ค่าเฉลี่ยของการแจกแจงคือ แล
ความแปรปรวนของการแจกแจงก็คือ แล
ค่าเบี่ยงเบนมาตรฐานของการแจกแจงคือ √ แล
ตัวอย่างเช่น สมมติว่าโรงพยาบาลมีการคลอดบุตรโดยเฉลี่ย 2 คนต่อชั่วโมง
จำนวนการเกิดโดยเฉลี่ยที่คาดหวังในชั่วโมงที่กำหนดคือ แล = การเกิด 2 ครั้ง
ความแปรปรวนของจำนวนการเกิดที่เราคาดหวังคือ แล = การเกิด 2 ครั้ง
ปัญหาการปฏิบัติการกระจายพันธุ์ปลา
ใช้แบบฝึกหัดแก้ปัญหาต่อไปนี้เพื่อทดสอบความรู้เกี่ยวกับการแจกแจงแบบปัวซอง
หมายเหตุ: เราจะใช้ เครื่องคำนวณการแจกแจงแบบปัวซอง เพื่อคำนวณคำตอบสำหรับคำถามเหล่านี้
ปัญหาที่ 1
คำถาม: เรารู้ว่าเว็บไซต์บางแห่งทำยอดขายได้ 10 ครั้งต่อชั่วโมง ในชั่วโมงที่กำหนด ความน่าจะเป็นที่ไซต์จะทำยอดขายได้ 8 ขีดเป็นเท่าใด
คำตอบ: การใช้เครื่องคำนวณการแจกแจงแบบปัวซองโดยมีค่า แล = 10 และ x = 8 เราจะพบว่า P(X=8) = 0.1126
ปัญหาที่ 2
คำถาม: เรารู้ว่าตัวแทนอสังหาริมทรัพย์บางรายมียอดขายเฉลี่ย 5 รายการต่อเดือน ในเดือนหนึ่งๆ ความน่าจะเป็นที่เธอจะทำยอดขายได้มากกว่า 7 ชิ้นเป็นเท่าใด
คำตอบ: การใช้เครื่องคำนวณการแจกแจงแบบปัวซงโดยมีค่า แล = 5 และ x = 7 เราจะพบว่า P(X>7) = 0.13337
ปัญหา 3
คำถาม: เรารู้ว่าโรงพยาบาลบางแห่งมีการคลอด 4 ครั้งต่อชั่วโมง ในชั่วโมงที่กำหนด ความน่าจะเป็นที่จะเกิด 4 ครั้งหรือน้อยกว่านั้นเป็นเท่าใด
คำตอบ: การใช้เครื่องคำนวณการแจกแจงแบบปัวซองด้วย แล = 4 และ x = 4 เราจะพบว่า P(X≤4) = 0.62884
แหล่งข้อมูลเพิ่มเติม
บทความต่อไปนี้จะอธิบายวิธีใช้การแจกแจงแบบปัวซองในซอฟต์แวร์ทางสถิติต่างๆ:
วิธีใช้การแจกแจงปัวซองใน R
วิธีใช้การกระจายปัวซองใน Excel
วิธีการคำนวณความน่าจะเป็นปัวซองบนเครื่องคิดเลข TI-84
ตัวอย่างการแจกแจงปัวซองในโลกแห่งความเป็นจริง
เครื่องคำนวณการกระจายตัวของปลา