สนีเดคคอร์ เอฟ ดิสทริบิวชั่น

โดย สิงหาคม 4, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจง Snedecor F คืออะไร และใช้เพื่ออะไร นอกจากนี้ คุณจะสามารถดูกราฟการกระจายของ Snedecor F และคุณสมบัติทางสถิติของกราฟนั้นได้

การกระจาย Snedecor F คืออะไร?

การแจกแจงแบบ Snedecor F หรือเรียกอีกอย่างว่า การแจกแจงแบบ Fisher–Snedecor F หรือเรียกง่ายๆ ว่า การแจกแจงแบบ F เป็นการแจกแจงความน่าจะเป็นแบบต่อเนื่องที่ใช้ในการอนุมานทางสถิติ โดยเฉพาะในการวิเคราะห์ความแปรปรวน

คุณสมบัติอย่างหนึ่งของการแจกแจง Snedecor F คือถูกกำหนดโดยค่าของพารามิเตอร์จริงสองตัวคือ m และ n ซึ่งระบุระดับความเป็นอิสระของพวกมัน ดังนั้น สัญลักษณ์ของการแจกแจง Snedecor F คือ F m,n โดยที่ m และ n คือพารามิเตอร์ที่กำหนดการแจกแจง

F_{m,n}\qquad m,n>0″ title=”Rendered by QuickLaTeX.com” height=”18″ width=”139″ style=”vertical-align: -6px;”></p> </p> <p> ในทางคณิตศาสตร์ การแจกแจงของ Snedecor F เท่ากับผลหารระหว่างการแจกแจงแบบไคสแควร์หนึ่งกับระดับความอิสระของมัน หารด้วยผลหารระหว่างการแจกแจงแบบไคสแควร์อีกอันหนึ่งกับระดับความอิสระของมัน ดังนั้นสูตรที่กำหนดการกระจาย Snedecor F จึงเป็นดังนี้: </p> </p> <p class=\left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}

การกระจายตัวของ Fisher-Snedecor F เป็นชื่อของนักสถิติชาวอังกฤษ Ronald Fisher และ George Snedecor นักสถิติชาวอเมริกัน

ในเชิงสถิติ การแจกแจงของ Fisher-Snedecor F มีการใช้งานที่แตกต่างกัน ตัวอย่างเช่น การแจกแจง Fisher-Snedecor F ใช้เพื่อเปรียบเทียบแบบจำลองการถดถอยเชิงเส้นต่างๆ และการแจกแจงความน่าจะเป็นนี้ใช้ในการวิเคราะห์ความแปรปรวน (ANOVA)

แผนภาพการกระจาย Snedecor F

เมื่อเราได้เห็นคำจำกัดความของการแจกแจงแบบ Snedecor F แล้ว กราฟของฟังก์ชันความหนาแน่นและกราฟของความน่าจะเป็นสะสมจะแสดงไว้ด้านล่าง

ในกราฟด้านล่าง คุณสามารถดูตัวอย่างการแจกแจง Snedecor F ที่มีระดับความอิสระต่างกันได้

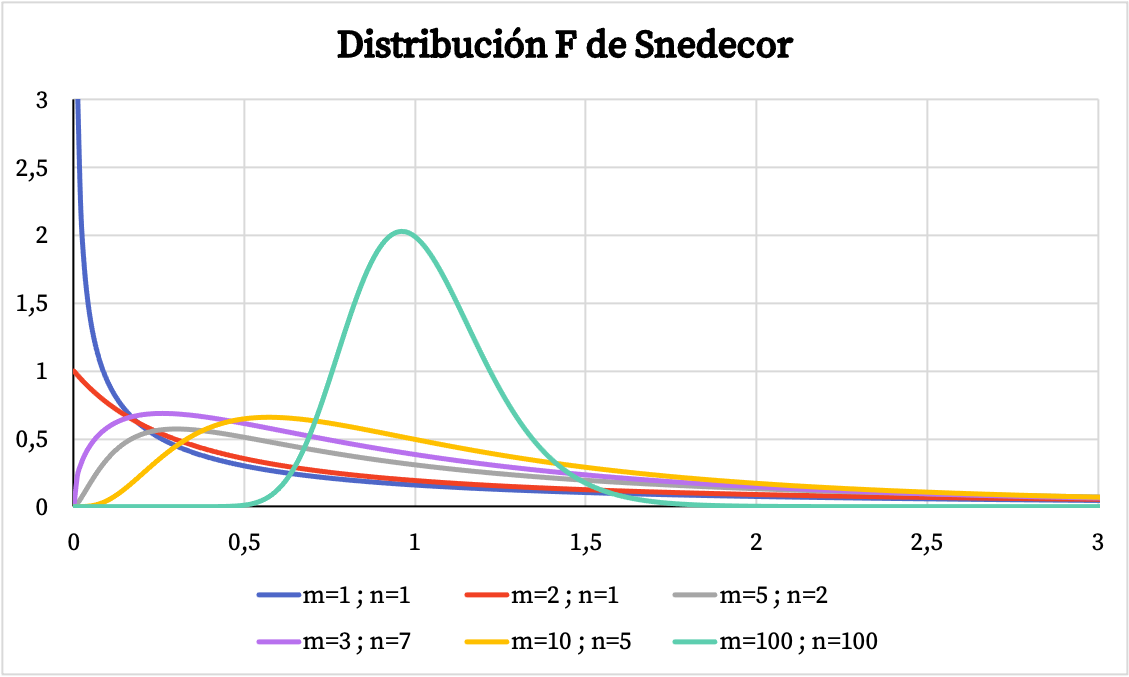
กราฟการกระจาย Snedecor F

ในทางกลับกัน ในกราฟด้านล่าง คุณจะเห็นว่ากราฟของฟังก์ชันความน่าจะเป็นสะสมของการแจกแจง Snedecor F แตกต่างกันไปตามค่าลักษณะเฉพาะของมันอย่างไร

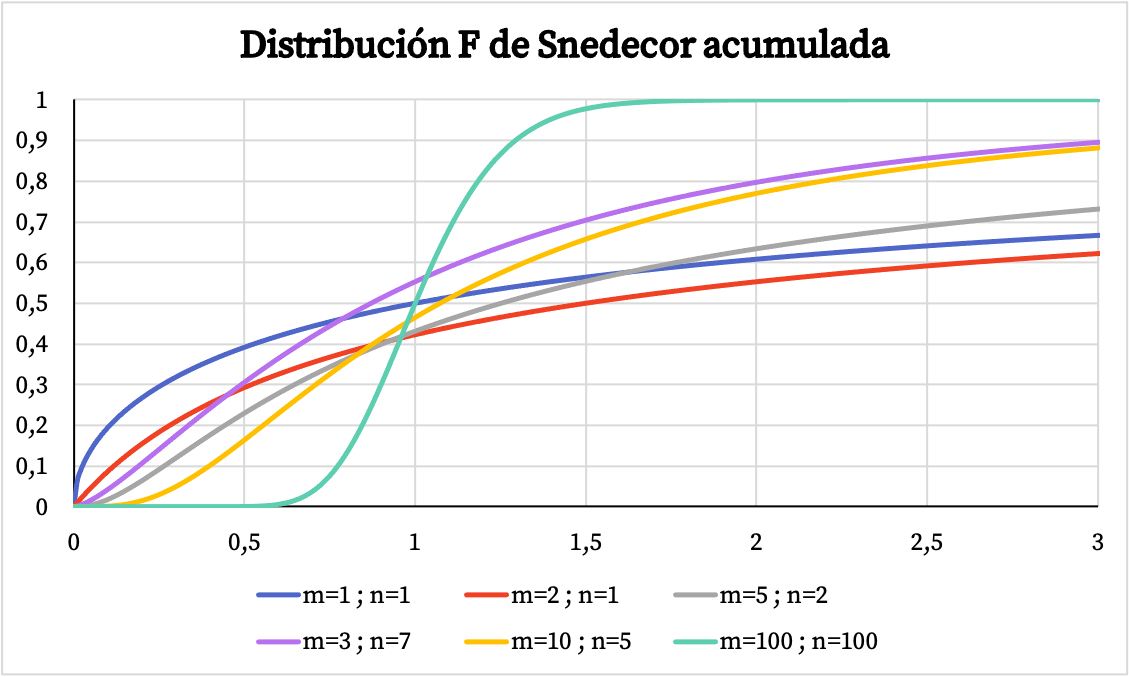
ความน่าจะเป็นสะสมของการแจกแจง Snedecor F

ลักษณะของการกระจาย Snedecor F

สุดท้ายนี้ ส่วนนี้จะนำเสนอคุณลักษณะที่สำคัญที่สุดของการกระจาย Snedecor F

  • องศาอิสระของการแจกแจง Snedecor F, m และ n เป็นพารามิเตอร์สองตัวที่กำหนดรูปร่างของการแจกแจง ค่าคุณลักษณะเหล่านี้ของการแจกแจง Snedecor F เป็นจำนวนเต็มบวก

\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p> </p> <ul> <li> โดเมนของการแจกแจงแบบ Snedecor F ประกอบด้วยจำนวนจริงทั้งหมดที่มากกว่าหรือเท่ากับศูนย์</li> </ul> <p class=x\in [0,+\infty)

  • สำหรับค่า n ที่มากกว่า 2 ค่าเฉลี่ยของการแจกแจง Snedecor F จะเท่ากับ n จากการลบ n ลบ 2

\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p> </p> <ul> <li> เมื่อพารามิเตอร์ <em>n</em> มากกว่า 2 ความแปรปรวนของการแจกแจง Snedecor F สามารถคำนวณได้โดยใช้สูตรต่อไปนี้:</li> </ul> <p class=\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p> </p> <ul> <li> หากพารามิเตอร์ <em>m</em> มากกว่า 2 โหมดของการแจกแจง Snedecor F สามารถคำนวณได้ด้วยนิพจน์ต่อไปนี้:</li> </ul> <p class=Mo=\cfrac{m-2}{m}\cdot \cfrac{n}{n+2}\qquad \text{para }m>2″ title=”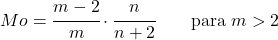Rendered by QuickLaTeX.com” height=”40″ width=”278″ style=”vertical-align: -14px;”></p> </p> <ul> <li> สูตรสำหรับฟังก์ชันความหนาแน่นของการแจกแจง Snedecor F มีดังนี้:</li> </ul> <p class=\displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}

  • หากตัวแปรเป็นไปตามการแจกแจงแบบ Snedecor F ด้วยดีกรีอิสระ m และ n ดังนั้นค่าผกผันของตัวแปรดังกล่าวจะเป็นไปตามการแจกแจงแบบ Snedecor F ด้วยดีกรีอิสระที่เท่ากันแต่เปลี่ยนลำดับของค่า

X\sim F_{m,n} \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^{-1}\sim F_{n,m}

  • การแจกแจงนักเรียนมีความสัมพันธ์ดังต่อไปนี้กับการแจกแจง Snedecor F:

X\sim t_n \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^2\sim F_{1,n}

เกี่ยวกับผู้แต่ง

Dr. Benjamin Anderson
ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

เพิ่มความคิดเห็น

อีเมลของคุณจะไม่แสดงให้คนอื่นเห็น ช่องข้อมูลจำเป็นถูกทำเครื่องหมาย *