การกระจายตัวอย่าง

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการกระจายตัวอย่างในสถิติคืออะไร และใช้เพื่ออะไร ดังนั้นคุณจะพบความหมายของการกระจายตัวอย่าง ตัวอย่างที่ชัดเจนของการกระจายตัวอย่าง และสูตรเพิ่มเติมสำหรับการแจกแจงตัวอย่างประเภทที่พบบ่อยที่สุด

การกระจายตัวอย่างคืออะไร?

การกระจายตัวอย่าง หรือ การกระจายตัวอย่าง คือการกระจายที่เป็นผลจากการพิจารณาตัวอย่างที่เป็นไปได้ทั้งหมดจากประชากร กล่าวอีกนัยหนึ่ง การกระจายตัวอย่างคือการกระจายที่ได้รับจากการคำนวณพารามิเตอร์การสุ่มตัวอย่างที่เป็นไปได้ทั้งหมดจากประชากร

ตัวอย่างเช่น ถ้าเราแยกตัวอย่างที่เป็นไปได้ทั้งหมดออกจากประชากรทางสถิติและคำนวณค่าเฉลี่ยของแต่ละตัวอย่าง ชุดของค่าเฉลี่ยของตัวอย่างจะก่อให้เกิดการแจกแจงตัวอย่าง แม่นยำยิ่งขึ้น เนื่องจากพารามิเตอร์ที่คำนวณได้คือค่าเฉลี่ยเลขคณิต จึงเป็นการกระจายตัวตัวอย่างของค่าเฉลี่ย

ในสถิติ การกระจายตัวอย่างใช้เพื่อคำนวณความน่าจะเป็นที่จะเข้าใกล้ค่าพารามิเตอร์ประชากรเมื่อศึกษาตัวอย่างเดียว ในทำนองเดียวกัน การกระจายตัวอย่างช่วยให้เราสามารถประมาณค่าข้อผิดพลาดในการสุ่มตัวอย่างสำหรับขนาดตัวอย่างที่กำหนดได้

ตัวอย่างการกระจายตัวอย่าง

ตอนนี้เราทราบคำจำกัดความของการกระจายตัวอย่างแล้ว เรามาดูตัวอย่างง่ายๆ เพื่อทำความเข้าใจแนวคิดนี้อย่างถ่องแท้กันดีกว่า

ในกล่องเราใส่ลูกบอล 3 ลูก แต่ละลูกมีตัวเลขเขียนตั้งแต่ 1 ถึง 3 โดยลูกหนึ่งมีหมายเลข 1 อีกลูกหนึ่งมีหมายเลข 2 และลูกสุดท้ายมีหมายเลข 3 สำหรับตัวอย่างขนาด n = 2 คำนวณความน่าจะเป็นของการกระจายตัวตัวอย่างของค่าเฉลี่ย หากเลือกตัวอย่างที่มีการแทนที่

ตัวอย่างจะถูกเลือกพร้อมการทดแทน นั่นคือ ลูกบอลที่หยิบขึ้นมาเพื่อเลือกองค์ประกอบแรกของตัวอย่างจะถูกส่งกลับไปยังกล่องและสามารถเลือกได้อีกครั้งในระหว่างการสกัดครั้งที่สอง ดังนั้น ตัวอย่างที่เป็นไปได้ทั้งหมดจากประชากรคือ:

1.1 1.2 1.3
2.1 2.2 2.3
3.1 3.2 3.3

ดังนั้นเราจึงคำนวณค่าเฉลี่ยเลขคณิตของแต่ละตัวอย่างที่เป็นไปได้:

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

ดังนั้น ความน่าจะเป็นที่จะได้แต่ละค่าของค่าเฉลี่ยตัวอย่างเมื่อเลือกตัวอย่างสุ่มจากประชากรจึงเป็นดังนี้

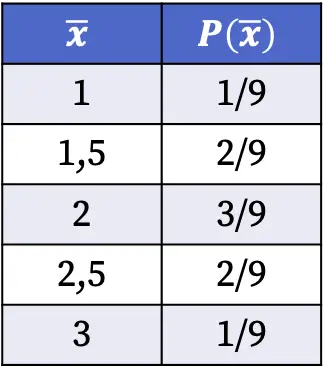
ความน่าจะเป็นของการกระจายตัวอย่างที่แสดงในตารางด้านบนคำนวณโดยการหารจำนวนตัวอย่างที่มีค่าเฉลี่ยดังกล่าวด้วยจำนวนกรณีที่เป็นไปได้ทั้งหมด ตัวอย่างเช่น: ค่าเฉลี่ยตัวอย่างคือ 1.5 ในสองกรณีจากเก้าที่เป็นไปได้ ดังนั้น P(1.5)=2/9

ประเภทของการกระจายตัวอย่าง

การแจกแจงการสุ่มตัวอย่าง (หรือการแจกแจงการสุ่มตัวอย่าง) สามารถจำแนกตามพารามิเตอร์การสุ่มตัวอย่างที่ได้รับ ดังนั้นประเภทการแจกแจงที่พบบ่อยที่สุดมีดังนี้:

การกระจายตัวอย่างค่าเฉลี่ย : นี่คือการกระจายตัวอย่างที่เกิดจากการคำนวณค่าเฉลี่ยเลขคณิตของแต่ละตัวอย่าง
การกระจายตัวอย่างตามสัดส่วน : เป็นการกระจายตัวอย่างที่ได้จากการคำนวณสัดส่วนของกลุ่มตัวอย่างทั้งหมด
การกระจายตัวอย่างความแปรปรวน : นี่คือการกระจายตัวอย่างที่สร้างชุดของความแปรปรวนทั้งหมดในตัวอย่าง
ความแตกต่างของค่าเฉลี่ยการกระจายตัวอย่าง : คือการกระจายตัวอย่างที่เกิดจากการคำนวณความแตกต่างระหว่างค่าเฉลี่ยของกลุ่มตัวอย่างที่เป็นไปได้ทั้งหมดจากประชากรสองกลุ่มที่แตกต่างกัน
ความแตกต่างในการกระจายตัวอย่างตามสัดส่วน : คือการกระจายตัวอย่างที่ได้รับโดยการลบสัดส่วนตัวอย่างที่เป็นไปได้ทั้งหมดออกจากประชากรสองกลุ่ม

การกระจายตัวอย่างแต่ละประเภทมีคำอธิบายโดยละเอียดด้านล่าง

การกระจายตัวอย่างค่าเฉลี่ย

เมื่อพิจารณาจากประชากรที่เป็นไปตามการแจกแจงความน่าจะเป็นแบบปกติด้วยค่าเฉลี่ย

$\mu$

และค่าเบี่ยงเบนมาตรฐาน

$\sigma$

และดึงตัวอย่างขนาดออกมา

$n$

การกระจายตัวตัวอย่างของค่าเฉลี่ยจะถูกกำหนดโดยการแจกแจงแบบปกติที่มีลักษณะดังต่อไปนี้:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

ทอง

$\mu_{\overline{x}}$

คือค่าเฉลี่ยของการกระจายตัวตัวอย่างของค่าเฉลี่ยและ

$\sigma_{\overline{x}}$

คือค่าเบี่ยงเบนมาตรฐาน นอกจากนี้,

$\cfrac{\sigma}{\sqrt{n}}$

คือค่าคลาดเคลื่อนมาตรฐานของการกระจายตัวตัวอย่าง

หมายเหตุ: หากประชากรไม่เป็นไปตามการแจกแจงแบบปกติแต่ขนาดของกลุ่มตัวอย่างมีขนาดใหญ่ (n>30) การกระจายตัวตัวอย่างของค่าเฉลี่ยก็สามารถประมาณได้กับการแจกแจงแบบปกติด้านบนด้วยขีดจำกัดทฤษฎีบทกลาง

ดังนั้น เนื่องจากการกระจายตัวตัวอย่างของค่าเฉลี่ยเป็นไปตามการแจกแจงแบบปกติ สูตรในการคำนวณความน่าจะเป็นใดๆ ที่เกี่ยวข้องกับค่าเฉลี่ยตัวอย่าง จึงเป็นดังนี้:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

ทอง:

$\overline{x}$

คือค่าเฉลี่ยตัวอย่าง
$\mu$

นี่คือค่าเฉลี่ยประชากร
$s$

คือค่าเบี่ยงเบนมาตรฐานประชากร
$n$

คือขนาดตัวอย่าง
$Z$

เป็นตัวแปรที่กำหนดโดยการแจกแจงแบบปกติมาตรฐาน N(0,1)

➤ ดู: แบบฝึกหัดที่แก้ไขแล้วเกี่ยวกับการแจกแจงสุ่มตัวอย่างของค่าเฉลี่ย

การกระจายตัวอย่างตามสัดส่วน

ที่จริงแล้ว เมื่อเราศึกษาสัดส่วนของกลุ่มตัวอย่าง เราจะวิเคราะห์กรณีความสำเร็จ ดังนั้น ตัวแปรสุ่มในการศึกษาจึงเป็นไปตามการแจกแจงความน่าจะเป็นแบบทวินาม

ตามทฤษฎีบทขีดจำกัดกลาง สำหรับขนาดใหญ่ (n>30) เราสามารถทำให้การแจกแจงแบบทวินามเข้าใกล้การแจกแจงแบบปกติมากขึ้น ดังนั้น การกระจายตัวอย่างตามสัดส่วนจะใกล้เคียงกับการแจกแจงแบบปกติด้วยพารามิเตอร์ต่อไปนี้:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

ทอง

$p$

คือความน่าจะเป็นของความสำเร็จและ

$q$

คือความน่าจะเป็นที่จะล้มเหลว

$q=1-p$

หมายเหตุ: การแจกแจงแบบทวินามสามารถประมาณได้เฉพาะกับการแจกแจงแบบปกติเท่านั้น

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”></p> <p> ,</p> <p class=$ $np\ge 5$

และ

$nq\ge 5$

ดังนั้น เนื่องจากการกระจายตัวของสัดส่วนตัวอย่างสามารถประมาณได้กับการแจกแจงแบบปกติ สูตรในการคำนวณความน่าจะเป็นใดๆ ที่เกี่ยวข้องกับสัดส่วนของกลุ่มตัวอย่าง จึงเป็นดังนี้:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

ทอง:

$\widehat{p}$

คือสัดส่วนตัวอย่าง
$p$

คือสัดส่วนของประชากร
$q$

คือความน่าจะเป็นที่จะล้มเหลวของประชากร

$q=1-p$

.
$n$

คือขนาดตัวอย่าง
$Z$

เป็นตัวแปรที่กำหนดโดยการแจกแจงแบบปกติมาตรฐาน N(0,1)

➤ ดู: แบบฝึกหัดแก้ไขเรื่องการกระจายตัวอย่างตามสัดส่วน

การกระจายตัวอย่างความแปรปรวน

การกระจายตัวอย่างความแปรปรวนถูกกำหนดโดยการแจกแจงความน่าจะเป็นแบบไคสแควร์ ดังนั้น สูตรสำหรับสถิติการกระจายตัวอย่างความแปรปรวน คือ:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

ทอง:

$\chi^2$

คือสถิติของการกระจายตัวตัวอย่างของความแปรปรวน ซึ่งเป็นไปตามการแจกแจงแบบไคสแควร์
$n$

คือขนาดตัวอย่าง
$s^2$

คือความแปรปรวนตัวอย่าง
$\sigma^2$

คือความแปรปรวนของประชากร

➤ ดู: แบบฝึกหัดที่แก้ไขแล้วเกี่ยวกับการกระจายตัวอย่างความแปรปรวน

การสุ่มตัวอย่างการกระจายตัวของผลต่างของค่าเฉลี่ย

หากขนาดตัวอย่างใหญ่เพียงพอ (n ₁ ≥30 และ n ₂ ≥30) การกระจายตัวตัวอย่างของผลต่างเฉลี่ยจะเป็นไปตามการแจกแจงแบบปกติ แม่นยำยิ่งขึ้นพารามิเตอร์ของการแจกแจงดังกล่าวจะถูกคำนวณดังนี้:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

หมายเหตุ: หากประชากรทั้งสองเป็นการแจกแจงแบบปกติ การกระจายตัวตัวอย่างของความแตกต่างในค่าเฉลี่ยจะเป็นไปตามการแจกแจงแบบปกติโดยไม่คำนึงถึงขนาดตัวอย่าง

ดังนั้น เนื่องจากการกระจายตัวตัวอย่างของความแตกต่างในค่าเฉลี่ยถูกกำหนดโดยการแจกแจงแบบปกติ สูตรในการคำนวณสถิติของการกระจายตัวอย่างของความแตกต่าง ในค่าเฉลี่ยจึงเป็นดังนี้

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

ทอง:

$\overline{x_i}$

คือค่าเฉลี่ยของกลุ่มตัวอย่าง i
$\mu_i$

คือค่าเฉลี่ยของประชากร i
$\sigma_i$

คือค่าเบี่ยงเบนมาตรฐานของประชากร i
$n_i$

คือขนาดตัวอย่าง i
$Z$

เป็นตัวแปรที่กำหนดโดยการแจกแจงแบบปกติมาตรฐาน N(0,1)

โปรดทราบว่าตัวอย่างจากประชากรที่แตกต่างกันอาจมีขนาดตัวอย่างที่แตกต่างกัน

➤ ดู: แบบฝึกหัดที่แก้ไขแล้วเกี่ยวกับการกระจายตัวตัวอย่างของผลต่างของค่าเฉลี่ย

การกระจายตัวอย่างความแตกต่างในสัดส่วน

ตัวอย่างที่เลือกสำหรับความแตกต่างในสัดส่วนของการกระจายตัวอย่างจะถูกกำหนดโดยการแจกแจงแบบทวินาม เนื่องจากในทางปฏิบัติ สัดส่วนคืออัตราส่วนของกรณีความสำเร็จต่อจำนวนการสังเกตทั้งหมด

อย่างไรก็ตาม เนื่องจากทฤษฎีบทขีดจำกัดกลาง การแจกแจงแบบทวินามจึงสามารถประมาณได้กับการแจกแจงความน่าจะเป็นแบบปกติ ดังนั้นการกระจายตัวอย่างส่วนต่างในสัดส่วนสามารถประมาณได้กับการแจกแจงแบบปกติโดยมีลักษณะดังต่อไปนี้

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

หมายเหตุ: การกระจายตัวตัวอย่างของความแตกต่างในสัดส่วนสามารถประมาณได้เฉพาะกับการแจกแจงแบบปกติเท่านั้น

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

และ

$n_2q_2\geq5$

ดังนั้น เนื่องจากการกระจายตัวตัวอย่างของส่วนต่างในสัดส่วนสามารถประมาณได้กับการแจกแจงแบบปกติ สูตรในการคำนวณสถิติของการกระจายตัวตัวอย่างของส่วนต่างในสัดส่วน จึงเป็นดังนี้

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

ทอง:

$\widehat{p_i}$

คือสัดส่วนตัวอย่าง i
$p_i$

คือสัดส่วนของประชากร i
$q_i$

คือความน่าจะเป็นที่จะเกิดความล้มเหลวของประชากร i

$q_i=1-p_i$

.
$n_i$

คือขนาดตัวอย่าง i
$Z$

เป็นตัวแปรที่กำหนดโดยการแจกแจงแบบปกติมาตรฐาน N(0,1)

➤ ดู: แบบฝึกหัดแก้ไขเรื่องการกระจายตัวอย่างส่วนต่างของสัดส่วน

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

การกระจายตัวอย่างคืออะไร?

ตัวอย่างการกระจายตัวอย่าง

ประเภทของการกระจายตัวอย่าง

การกระจายตัวอย่างค่าเฉลี่ย

การกระจายตัวอย่างตามสัดส่วน

การกระจายตัวอย่างความแปรปรวน

การสุ่มตัวอย่างการกระจายตัวของผลต่างของค่าเฉลี่ย

การกระจายตัวอย่างความแตกต่างในสัดส่วน

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น