วิธีการคำนวณการกระจายตัวอย่างใน excel

การกระจายตัวอย่าง คือการกระจายความน่าจะเป็นของ สถิติ บางอย่างโดยอิงจากตัวอย่างสุ่มจำนวนมากจาก ประชากรกลุ่ม เดียว

บทช่วยสอนนี้จะอธิบายวิธีการดำเนินการต่อไปนี้ด้วยการกระจายตัวอย่างใน Excel:

• สร้างการกระจายตัวอย่าง
• แสดงภาพการกระจายตัวอย่าง
• คำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของการกระจายตัวอย่าง
• คำนวณความน่าจะเป็นเกี่ยวกับการกระจายตัวอย่าง

สร้างการกระจายตัวอย่างใน Excel

สมมติว่าเราต้องการสร้างการกระจายตัวอย่างที่ประกอบด้วย 1,000 ตัวอย่าง โดยแต่ละขนาดตัวอย่างคือ 20 และมาจากการแจกแจงแบบปกติโดยมีค่าเฉลี่ย 5.3 และค่าเบี่ยงเบนมาตรฐาน 9

เราสามารถทำได้ง่ายๆ โดยพิมพ์สูตรต่อไปนี้ลงในเซลล์ A2 ของสเปรดชีตของเรา:

 = NORM . INV ( RAND (), 5.3, 9)

จากนั้นเราสามารถวางเมาส์เหนือมุมขวาล่างของเซลล์จนกระทั่งเครื่องหมาย + เล็กๆ ปรากฏขึ้น แล้วลากสูตรไปทางขวา 20 เซลล์และลงไป 1,000 เซลล์:

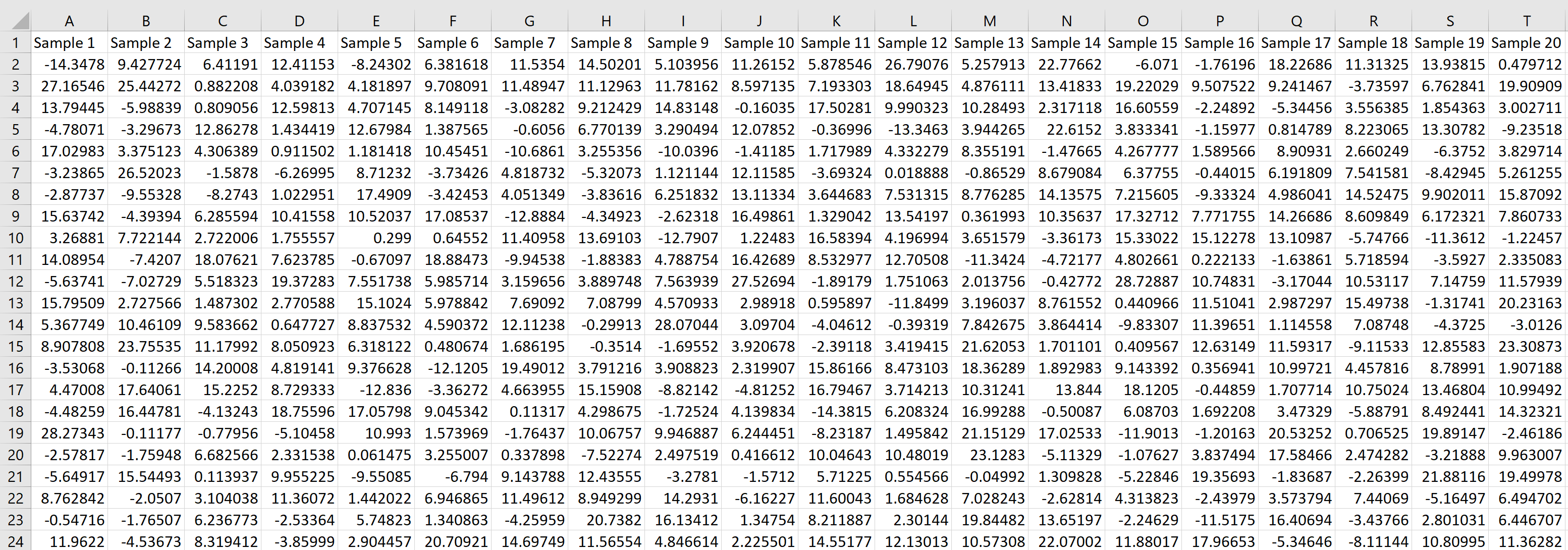
แต่ละแถวแสดงถึงตัวอย่างขนาด 20 โดยแต่ละค่ามาจากการแจกแจงแบบปกติโดยมีค่าเฉลี่ย 5.3 และค่าเบี่ยงเบนมาตรฐานคือ 9

ค้นหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน

ในการค้นหาค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐานของการกระจายตัวของตัวอย่างนี้ เราสามารถหาค่าเฉลี่ยของแต่ละตัวอย่างได้โดยพิมพ์สูตรต่อไปนี้ลงในเซลล์ U2 ของเวิร์กชีทของเรา:

 = AVERAGE (A2:T2)

จากนั้นเราสามารถวางเมาส์เหนือมุมขวาล่างของเซลล์จนกระทั่งเครื่องหมาย + เล็กๆ ปรากฏขึ้น จากนั้นดับเบิลคลิกเพื่อคัดลอกสูตรนี้ไปยังเซลล์อื่นๆ ทั้งหมดในคอลัมน์ U:

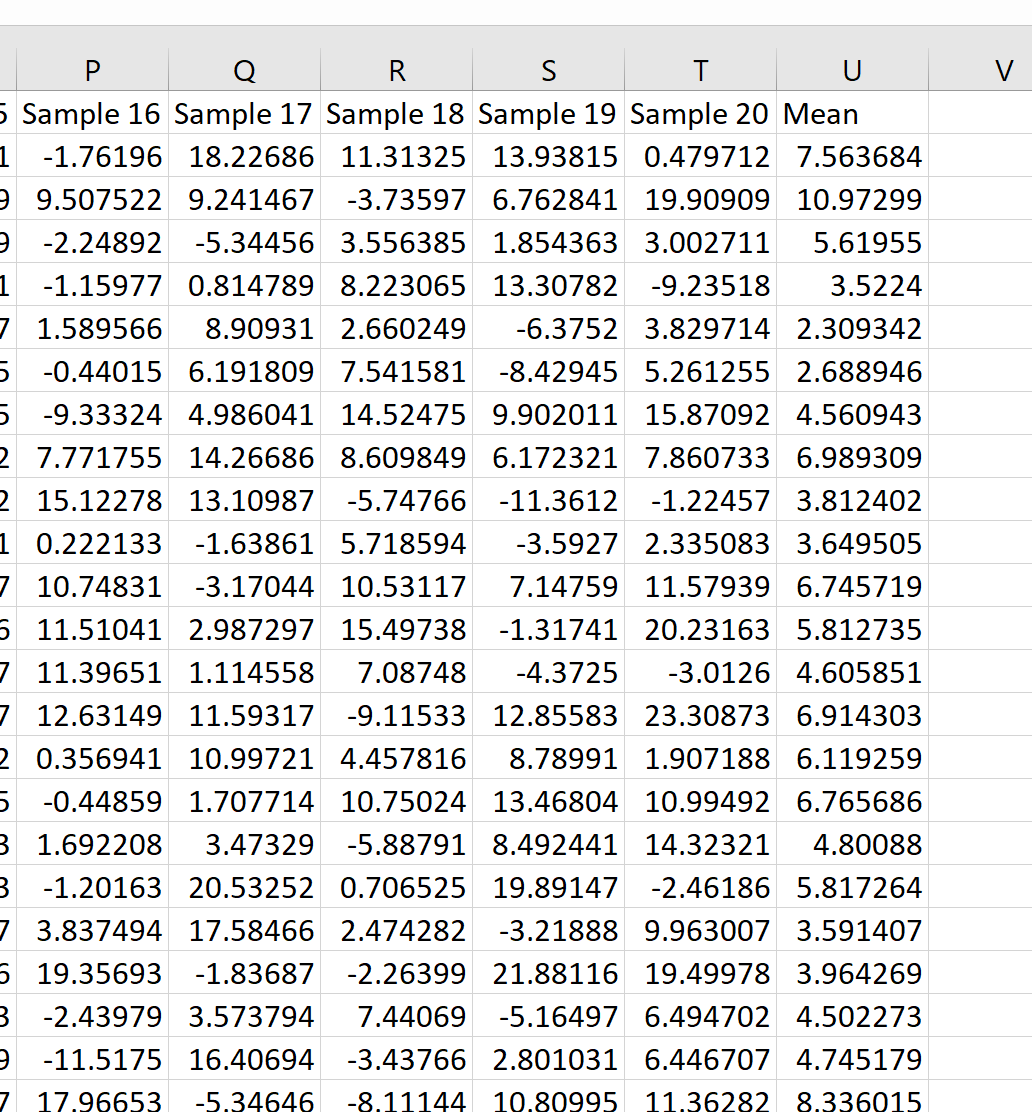
เราจะเห็นว่ากลุ่มตัวอย่างแรกมีค่าเฉลี่ย 7.563684 กลุ่มตัวอย่างที่สองมีค่าเฉลี่ย 10.97299 และอื่นๆ

จากนั้นเราสามารถใช้สูตรต่อไปนี้เพื่อคำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของค่าเฉลี่ยตัวอย่าง:

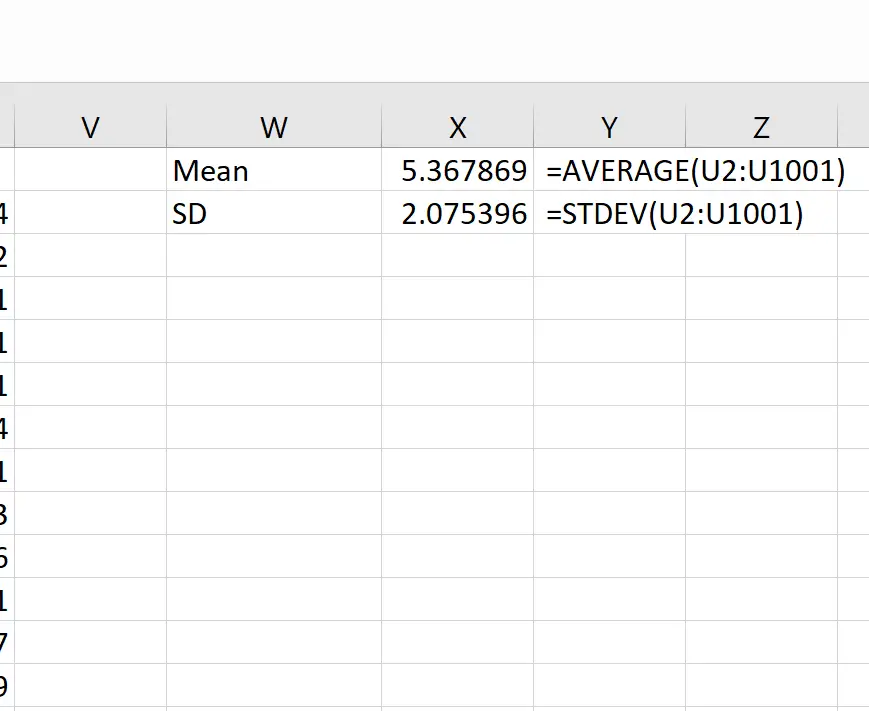
ตามทฤษฎีแล้ว ค่าเฉลี่ยของการกระจายตัวอย่างควรเป็น 5.3 เราจะเห็นว่าค่าเฉลี่ยตัวอย่างจริงในตัวอย่างนี้คือ 5.367869 ซึ่งใกล้เคียงกับ 5.3

และตามทฤษฎี ค่าเบี่ยงเบนมาตรฐานของการกระจายตัวอย่างควรเท่ากับ s/√n ซึ่งก็คือ 9 / √20 = 2.012 เราจะเห็นว่าค่าเบี่ยงเบนมาตรฐานที่แท้จริงของการกระจายตัวอย่างคือ 2.075396 ซึ่งใกล้เคียงกับ 2.012

แสดงภาพการกระจายตัวอย่าง

นอกจากนี้เรายังสามารถสร้างฮิสโตแกรมอย่างง่ายเพื่อให้เห็นภาพการกระจายตัวตัวอย่างของค่าเฉลี่ยตัวอย่าง

เมื่อต้องการทำเช่นนี้ เพียงเน้นค่าเฉลี่ยตัวอย่างทั้งหมดในคอลัมน์ U คลิกแท็บ แทรก จากนั้นคลิกตัวเลือก ฮิสโตแก รมใต้ส่วน แผนภูมิ

จะได้ฮิสโตแกรมดังต่อไปนี้:

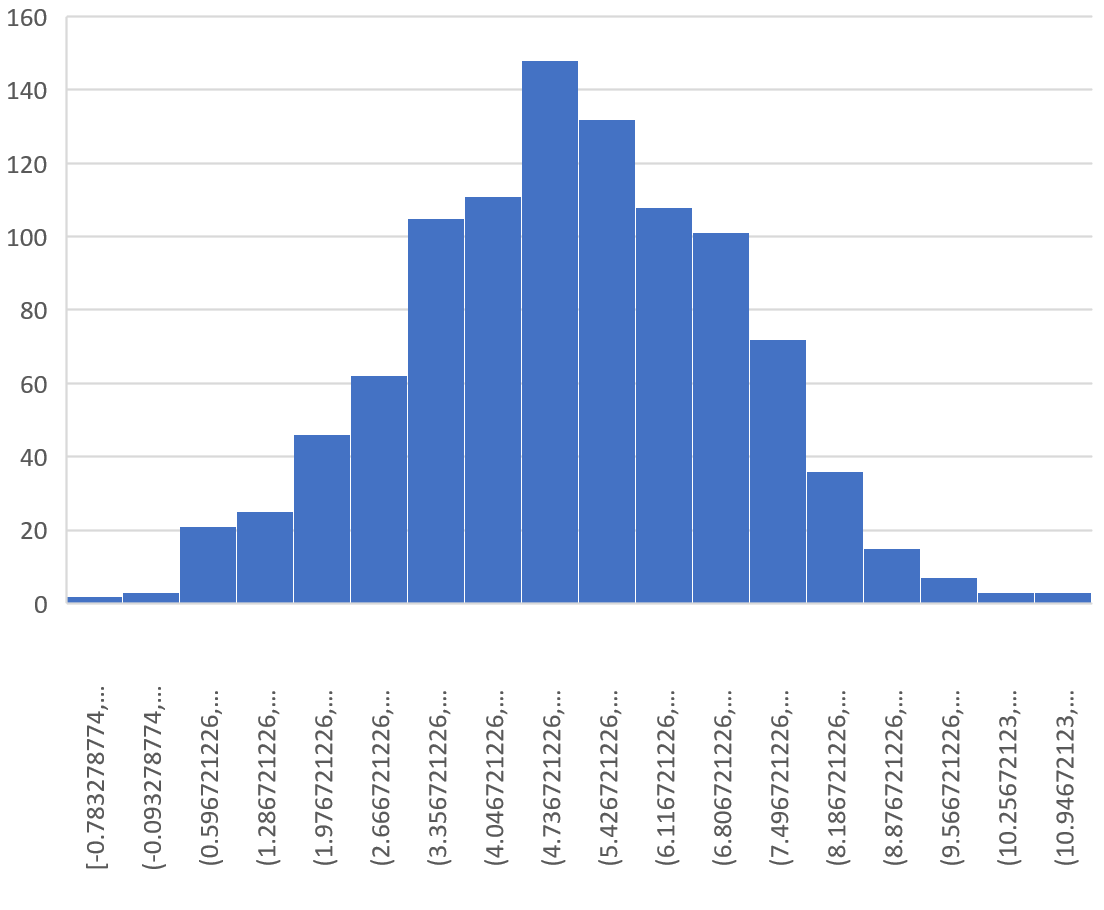
จะเห็นได้ว่าการกระจายตัวอย่างเป็นรูประฆังโดยมียอดใกล้ค่า 5

อย่างไรก็ตาม จากส่วนท้ายของการแจกแจง เราจะเห็นว่าตัวอย่างบางตัวอย่างมีค่าเฉลี่ยมากกว่า 10 และตัวอย่างอื่นๆ มีค่าเฉลี่ยน้อยกว่า 0

คำนวณความน่าจะเป็น

นอกจากนี้เรายังสามารถคำนวณความน่าจะเป็นที่จะได้ค่าที่แน่นอนสำหรับค่าเฉลี่ยตัวอย่าง โดยพิจารณาจากค่าเฉลี่ยประชากร ค่าเบี่ยงเบนมาตรฐานของประชากร และขนาดตัวอย่าง

ตัวอย่างเช่น เราสามารถใช้สูตรต่อไปนี้เพื่อค้นหาความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างน้อยกว่าหรือเท่ากับ 6 โดยที่ค่าเฉลี่ยประชากรคือ 5.3 ส่วนเบี่ยงเบนมาตรฐานของประชากรคือ 9 และขนาดตัวอย่างคือ:

 = COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)

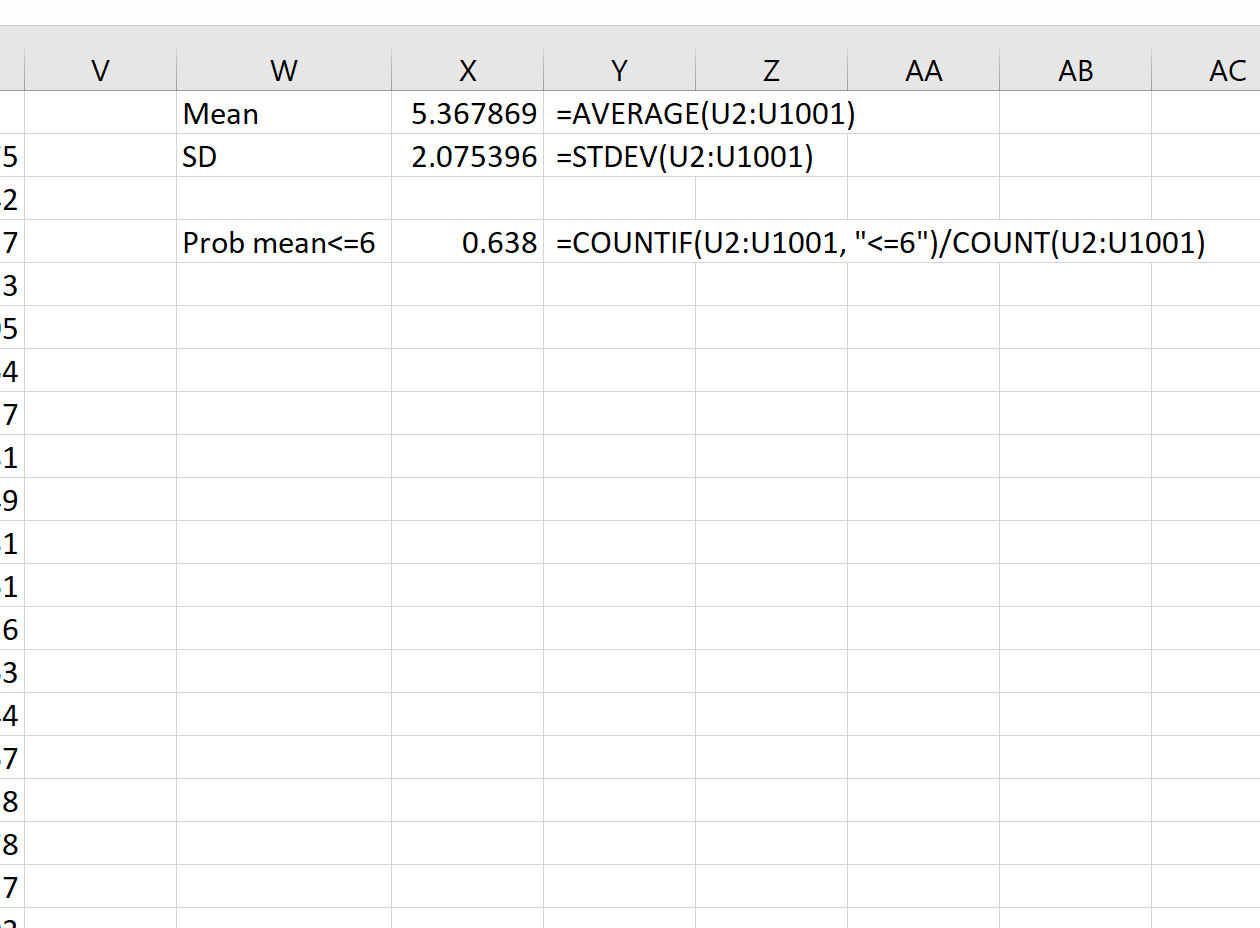
เราจะเห็นว่าความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างน้อยกว่าหรือเท่ากับ 6 คือ 0.638

ซึ่งใกล้เคียงกับความน่าจะเป็นที่คำนวณโดย Sampling Distribution Calculator :

แหล่งข้อมูลเพิ่มเติม

บทนำเกี่ยวกับการแจกแจงตัวอย่าง
เครื่องคำนวณการกระจายตัวอย่าง
ความรู้เบื้องต้นเกี่ยวกับทฤษฎีบทขีดจำกัดศูนย์กลาง