วิธีการคำนวณการแจกแจงการสุ่มตัวอย่างใน r

การกระจายตัวอย่าง คือการแจกแจงความน่าจะเป็นของ สถิติ บางอย่างโดยอิงจากตัวอย่างสุ่มจำนวนมากจากประชากรกลุ่มเดียว

บทช่วยสอนนี้จะอธิบายวิธีดำเนินการต่อไปนี้ด้วยการแจกแจงตัวอย่างใน R:

• สร้างการกระจายตัวอย่าง
• แสดงภาพการกระจายตัวอย่าง
• คำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของการกระจายตัวอย่าง
• คำนวณความน่าจะเป็นเกี่ยวกับการกระจายตัวอย่าง

สร้างการกระจายตัวอย่างใน R

รหัสต่อไปนี้แสดงวิธีการสร้างการกระจายตัวอย่างใน R:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656

ในตัวอย่างนี้ เราใช้ฟังก์ชัน rnorm() เพื่อคำนวณค่าเฉลี่ยของตัวอย่าง 10,000 ตัวอย่าง โดยแต่ละขนาดตัวอย่างคือ 20 และสร้างขึ้นจากการแจกแจงแบบปกติที่มีค่าเฉลี่ย 5.3 และค่าเบี่ยงเบนมาตรฐานเป็น 9

เราจะเห็นว่ากลุ่มตัวอย่างแรกมีค่าเฉลี่ย 5.283992 กลุ่มตัวอย่างที่สองมีค่าเฉลี่ย 6.304845 และอื่นๆ

แสดงภาพการกระจายตัวอย่าง

รหัสต่อไปนี้แสดงวิธีการสร้างฮิสโตแกรมอย่างง่ายเพื่อแสดงภาพการกระจายตัวอย่าง:

 #create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

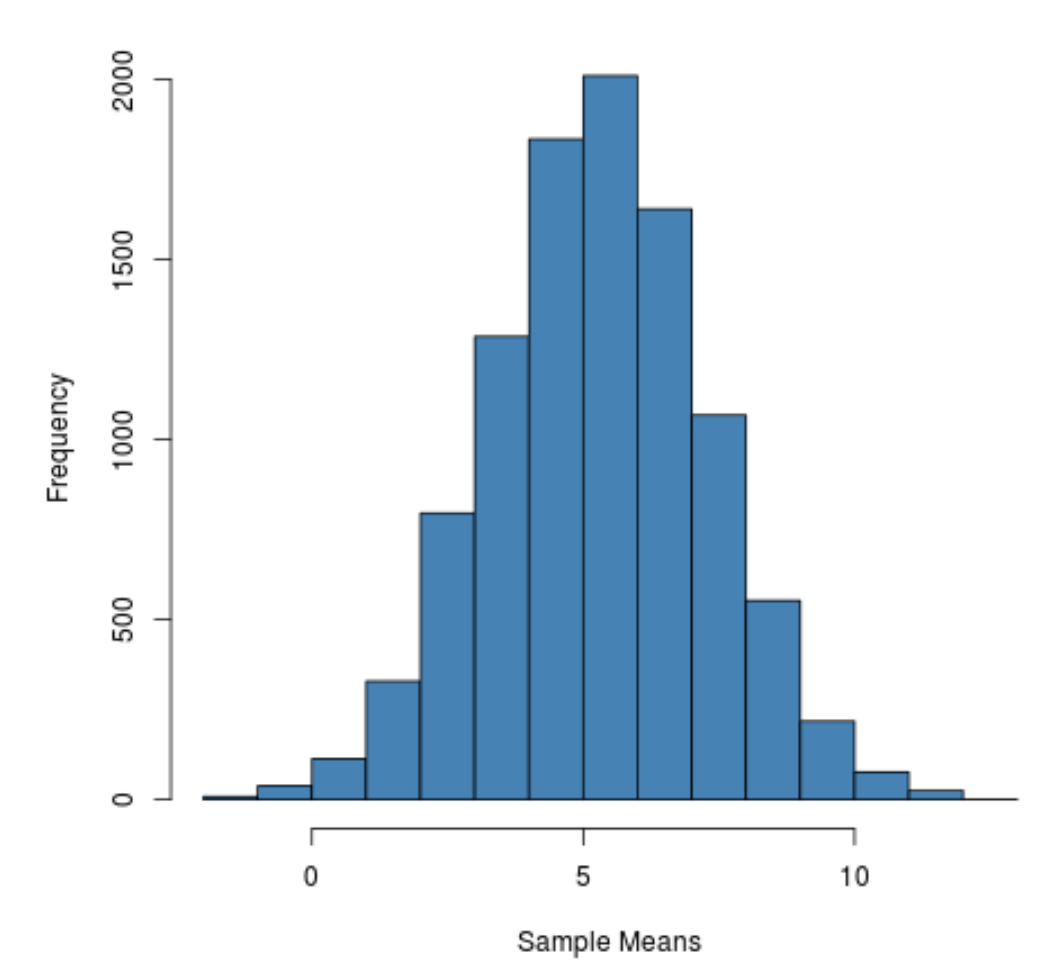
จะเห็นได้ว่าการกระจายตัวอย่างเป็นรูประฆังโดยมียอดใกล้ค่า 5

อย่างไรก็ตาม จากส่วนท้ายของการแจกแจง เราจะเห็นว่าตัวอย่างบางตัวอย่างมีค่าเฉลี่ยมากกว่า 10 และตัวอย่างอื่นๆ มีค่าเฉลี่ยน้อยกว่า 0

ค้นหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน

รหัสต่อไปนี้แสดงวิธีคำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของการกระจายตัวอย่าง:

 #mean of sampling distribution
mean(sample_means)

[1] 5.287195

#standard deviation of sampling distribution
sd(sample_means)

[1] 2.00224

ตามทฤษฎีแล้ว ค่าเฉลี่ยของการกระจายตัวอย่างควรเป็น 5.3 เราจะเห็นว่าค่าเฉลี่ยตัวอย่างจริงในตัวอย่างนี้คือ 5.287195 ซึ่งใกล้เคียงกับ 5.3

และตามทฤษฎี ค่าเบี่ยงเบนมาตรฐานของการกระจายตัวอย่างควรเท่ากับ s/√n ซึ่งก็คือ 9 / √20 = 2.012 เราจะเห็นว่าค่าเบี่ยงเบนมาตรฐานที่แท้จริงของการกระจายตัวอย่างคือ 2.00224 ซึ่งใกล้เคียงกับ 2.012

คำนวณความน่าจะเป็น

รหัสต่อไปนี้แสดงวิธีคำนวณความน่าจะเป็นที่จะได้ค่าที่แน่นอนสำหรับค่าเฉลี่ยตัวอย่าง โดยพิจารณาจากค่าเฉลี่ยประชากร ค่าเบี่ยงเบนมาตรฐานของประชากร และขนาดตัวอย่าง

 #calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

ในตัวอย่างนี้ เราค้นหาความน่าจะเป็นที่ค่าเฉลี่ยตัวอย่างน้อยกว่าหรือเท่ากับ 6 โดยที่ค่าเฉลี่ยประชากรคือ 5.3 ส่วนเบี่ยงเบนมาตรฐานของประชากรคือ 9 และขนาดของตัวอย่าง 20 คือ 0.6417

ซึ่งใกล้เคียงกับความน่าจะเป็นที่คำนวณโดย Sampling Distribution Calculator :

รหัสที่สมบูรณ์

รหัส R ที่สมบูรณ์ที่ใช้ในตัวอย่างนี้แสดงอยู่ด้านล่าง:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

#mean of sampling distribution
mean(sample_means)

#standard deviation of sampling distribution
sd(sample_means)

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

แหล่งข้อมูลเพิ่มเติม

บทนำเกี่ยวกับการแจกแจงตัวอย่าง
เครื่องคำนวณการกระจายตัวอย่าง
ความรู้เบื้องต้นเกี่ยวกับทฤษฎีบทขีดจำกัดศูนย์กลาง