การกระจายแบบปกติ

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจงแบบปกติในสถิติคืออะไร คุณจะพบคำจำกัดความของการแจกแจงแบบปกติ ตัวอย่างของการแจกแจงแบบปกติ และคุณสมบัติของการแจกแจงแบบปกติมีอะไรบ้าง

การแจกแจงแบบปกติคืออะไร?

การแจกแจงแบบปกติ คือการแจกแจงความน่าจะเป็นแบบต่อเนื่องซึ่งมีกราฟเป็นรูประฆังและสมมาตรเกี่ยวกับค่าเฉลี่ย ในทางสถิติ การแจกแจงแบบปกติจะใช้เพื่อสร้างแบบจำลองปรากฏการณ์ที่มีลักษณะเฉพาะที่แตกต่างกันมาก ซึ่งเป็นเหตุผลว่าทำไมการแจกแจงนี้จึงมีความสำคัญมาก

ที่จริงแล้ว ในเชิงสถิติ การแจกแจงแบบปกติถือเป็นการแจกแจงที่สำคัญที่สุดของการแจกแจงความน่าจะเป็นทั้งหมด เนื่องจากไม่เพียงแต่สามารถจำลองปรากฏการณ์ในโลกแห่งความเป็นจริงจำนวนมากได้เท่านั้น แต่การแจกแจงแบบปกติยังสามารถใช้เพื่อประมาณค่าการแจกแจงแบบปกติประเภทอื่นๆ ได้อีกด้วย การแจกแจง ภายใต้เงื่อนไขบางประการ

สัญลักษณ์สำหรับการแจกแจงแบบปกติคืออักษรตัวใหญ่ N ดังนั้นเพื่อระบุว่าตัวแปรเป็นไปตามการแจกแจงแบบปกติจึงถูกระบุด้วยตัวอักษร N และค่าของค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานจะถูกเพิ่มในวงเล็บ

$X\sim N(\mu,\sigma)$

การแจกแจงแบบปกติมีชื่อเรียกที่แตกต่างกันมากมาย เช่น การแจกแจงแบบเกาส์เซียน การแจกแจงแบบเกาส์เซียน และ การแจกแจงแบบลาปลาซ-เกาส์

ตัวอย่างของการแจกแจงแบบปกติ

โดยทั่วไป ชุดข้อมูลที่เป็นไปตามการแจกแจงแบบปกติจะมีข้อสังเกตจำนวนมากและครอบคลุมหัวข้อทั่วไปมาก ด้านล่างนี้คือตัวอย่างทางสถิติหลายตัวอย่างที่โดยทั่วไปสามารถสร้างแบบจำลองได้ด้วยการแจกแจงแบบปกติ

ตัวอย่างของการแจกแจงแบบปกติ:

ขนาดของนักเรียนในหลักสูตร
ไอคิวของพนักงานบริษัท
จำนวนชิ้นส่วนชำรุดที่ผลิตในโรงงานในหนึ่งวัน
คะแนนที่ได้รับจากการสอบของนักเรียนในรายวิชา
การทำกำไรของหุ้นของบริษัทที่จดทะเบียนในตลาดหลักทรัพย์

กราฟการแจกแจงแบบปกติ

เมื่อเราได้เห็นแล้วว่าการแจกแจงแบบปกติคืออะไรและตัวอย่างบางส่วนของการแจกแจงความน่าจะเป็นประเภทนี้ เรามาดูกันว่ากราฟจะเป็นอย่างไรเพื่อให้เข้าใจแนวคิดได้ดีขึ้น

ในกราฟต่อไปนี้ คุณจะเห็นว่าฟังก์ชันความหนาแน่นของการแจกแจงแบบปกติแตกต่างกันไปอย่างไร ขึ้นอยู่กับค่าของค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐาน

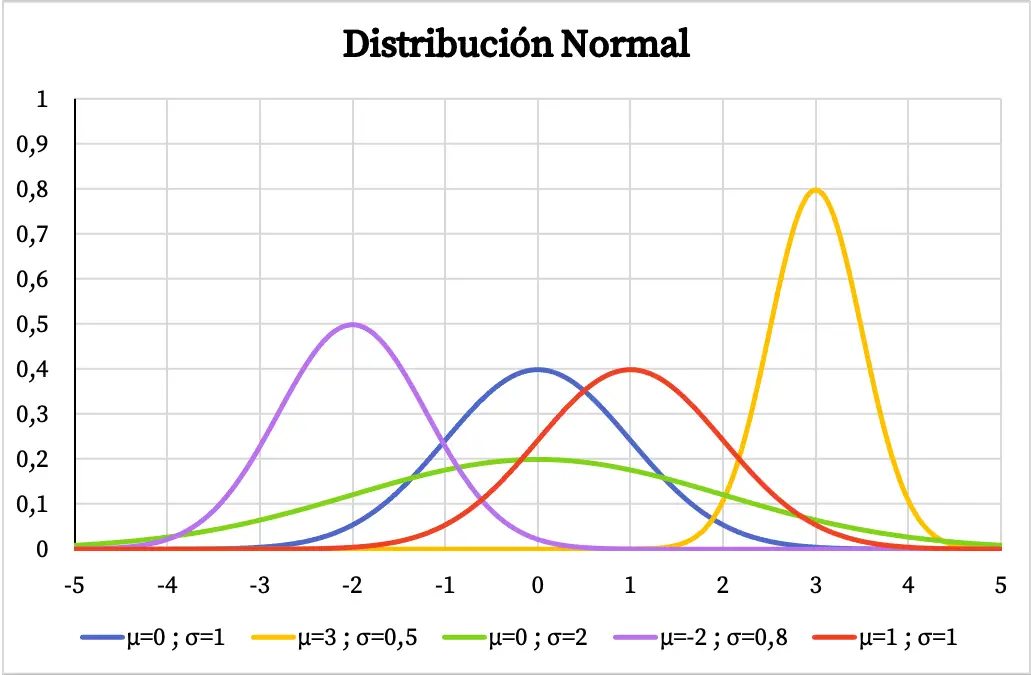
การมีรูประฆังอยู่ตรงกลางค่าเฉลี่ยเลขคณิต หากตัวแปรมีการแจกแจงแบบปกติ หมายความว่าค่าที่ซ้ำกันมากที่สุดคือค่าเฉลี่ย และค่ารอบค่าเฉลี่ยจะซ้ำบ่อยกว่าค่าสุดขั้ว ในทำนองเดียวกัน ยิ่งค่าเบี่ยงเบนมาตรฐานของการแจกแจงแบบปกติมากเท่าใด รูปร่างของการแสดงกราฟิกก็จะยิ่งสวยงามมากขึ้นเท่านั้น

ในทางกลับกัน กราฟของฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบปกติยังขึ้นอยู่กับค่าของค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานด้วย ดังที่คุณเห็นในภาพต่อไปนี้:

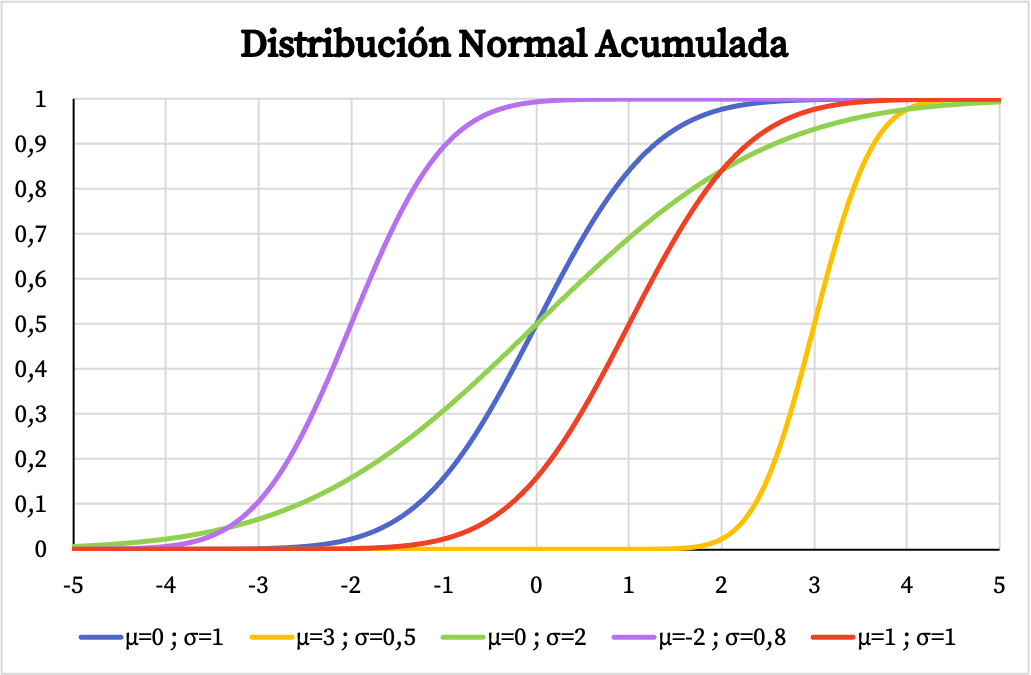
ฟังก์ชันความหนาแน่นและฟังก์ชันการกระจายของการแจกแจงแบบปกติทำให้สามารถคำนวณความน่าจะเป็นที่เชื่อมโยงกับการแจกแจงนี้ได้ อย่างไรก็ตาม แทนที่จะใช้สูตร คุณสามารถใช้ตารางการแจกแจงแบบปกติได้โดยตรงเนื่องจากเร็วกว่า คุณสามารถดูตารางเหล่านี้ได้ที่ลิงค์ต่อไปนี้:

➤ ดูที่: ตารางการแจกแจงแบบปกติ

ลักษณะของการแจกแจงแบบปกติ

การแจกแจงแบบปกติมีลักษณะดังต่อไปนี้:

การแจกแจงแบบปกติขึ้นอยู่กับพารามิเตอร์ลักษณะเฉพาะสองตัว ซึ่งได้แก่ ค่าเฉลี่ยเลขคณิต (μ) และค่าเบี่ยงเบนมาตรฐาน (σ)

$X\sim N(\mu,\sigma)$

การแจกแจงแบบปกติสามารถรับค่าบวกและลบได้ ดังนั้นโดเมนของการแจกแจงแบบปกติจึงประกอบด้วยจำนวนจริง

$x\in \mathbb{R}$

ค่ามัธยฐานและรูปแบบของการแจกแจงแบบปกติจะเท่ากับค่าเฉลี่ยเลขคณิตของการแจกแจง

$Me=Mo=\mu$

ค่าสัมประสิทธิ์ความเบ้และค่าสัมประสิทธิ์ความโด่งของการแจกแจงแบบปกติเป็นศูนย์

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

สูตรสำหรับฟังก์ชันความหนาแน่นของการแจกแจงแบบปกติคือ:

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

ในทำนองเดียวกัน สูตรสำหรับฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบปกติคือ:

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

การประยุกต์ใช้ทฤษฎีบทขีดจำกัดจุดศูนย์กลางก็คือ การแจกแจงแบบปัวซอง สามารถประมาณค่าการแจกแจงแบบปกติได้เมื่อค่าของ แล มีขนาดใหญ่เพียงพอ

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

การประยุกต์ใช้ทฤษฎีบทขีดจำกัดกลางอีกประการหนึ่งก็คือ การแจกแจงแบบทวินาม สามารถประมาณได้ด้วยการแจกแจงแบบปกติสำหรับชุดข้อมูลที่มีการสังเกตจำนวนมาก

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

การกระจายตัวแบบปกติมาตรฐาน

การแจกแจงแบบปกติมาตรฐาน หรือที่เรียกว่า การแจกแจงแบบปกติแบบหน่วย เป็นกรณีที่ง่ายที่สุดของการแจกแจงแบบปกติ แม่นยำยิ่งขึ้นการแจกแจงแบบปกติมาตรฐานคือการแจกแจงแบบปกติที่มีค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานเท่ากับ 0 และ 1 ตามลำดับ

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

โปรดทราบว่าการแจกแจงแบบปกติใดๆ สามารถแปลงเป็นการแจกแจงแบบปกติมาตรฐานได้โดยใช้กระบวนการที่เรียกว่าการพิมพ์ ซึ่งเกี่ยวข้องกับการลบค่าเฉลี่ยเลขคณิตออกจากแต่ละค่า แล้วหารด้วยค่าเบี่ยงเบนมาตรฐาน

นอกจากนี้ การแจกแจงแบบปกติมาตรฐานยังใช้เพื่อกำหนดความน่าจะเป็นของการแจกแจงแบบปกติโดยใช้ตารางความน่าจะเป็น ดังนั้น ในการค้นหาความน่าจะเป็นของการแจกแจงแบบปกติ ก่อนอื่นให้ป้อนตัวแปรเพื่อแปลงเป็นการแจกแจงแบบปกติมาตรฐาน จากนั้นเราจะดูในตารางเพื่อดูว่าค่าความน่าจะเป็นที่สอดคล้องกันคือเท่าใด หากต้องการข้อมูลเพิ่มเติม โปรดคลิกลิงก์ต่อไปนี้:

➤ โปรดดู: การแจกแจงแบบปกติมาตรฐาน

การกระจายตัวแบบปกติและกฎเชิงประจักษ์

ในสถิติ กฎ ทั่วไป หรือที่เรียกว่า กฎ 68-95-99.7 เป็นกฎที่กำหนดเปอร์เซ็นต์ของค่าในการแจกแจงแบบปกติซึ่งอยู่ภายในค่าเบี่ยงเบนมาตรฐานสามค่าของค่าเฉลี่ย

โดยเฉพาะอย่างยิ่งกฎทั่วไประบุดังต่อไปนี้:

68% ของค่าในการแจกแจงแบบปกติอยู่ภายในค่าเบี่ยงเบนมาตรฐานหนึ่งของค่าเฉลี่ย
95% ของค่าในการแจกแจงแบบปกติอยู่ภายในค่าเบี่ยงเบนมาตรฐานสองค่าของค่าเฉลี่ย
99.7% ของค่าในการแจกแจงแบบปกติอยู่ภายในค่าเบี่ยงเบนมาตรฐานสามค่าของค่าเฉลี่ย

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม