การกระจายตัวแบบไฮเปอร์เรขาคณิต
ในบทความนี้ เราจะอธิบายว่าการแจกแจงแบบไฮเปอร์เรขาคณิตคืออะไร และความน่าจะเป็นคำนวณด้วยการแจกแจงประเภทนี้อย่างไร คุณจะพบสูตรออนไลน์สำหรับการแจกแจงแบบไฮเปอร์จีโอเมตริก คุณลักษณะเฉพาะของมัน ตลอดจนเครื่องคิดเลขเพื่อคำนวณความน่าจะเป็นของการกระจายตัวแบบไฮเปอร์จีโอเมตริก
การกระจายตัวแบบไฮเปอร์เรขาคณิตคืออะไร?
การแจกแจงแบบไฮเปอร์เรขาคณิต คือการแจกแจงความน่าจะเป็นที่อธิบายจำนวนกรณีที่ประสบความสำเร็จในการสุ่มตัวอย่างโดยไม่ต้องแทนที่องค์ประกอบ n รายการจากประชากร
นั่นคือ การแจกแจงแบบไฮเปอร์เรขาคณิตใช้ในการคำนวณความน่าจะเป็นที่จะได้ x สำเร็จเมื่อแยกองค์ประกอบ n รายการออกจากประชากรโดยไม่ต้องแทนที่องค์ประกอบใดเลย
การกระจายแบบไฮเปอร์เรขาคณิตมีพารามิเตอร์สามตัว:
- N : คือจำนวนองค์ประกอบในประชากร (N = 0, 1, 2,…)
- K : คือจำนวนกรณีความสำเร็จสูงสุด (K = 0, 1, 2,…,N) เนื่องจากในการกระจายแบบไฮเปอร์เรขาคณิต องค์ประกอบสามารถพิจารณาได้ว่าเป็น “ความสำเร็จ” หรือ “ความล้มเหลว” เท่านั้น NK จึงเป็นจำนวนกรณีความล้มเหลวสูงสุด
- n : คือจำนวนการดึงข้อมูลที่ไม่มีการแทนที่ที่ดำเนินการ
![]()
ตัวอย่างเช่น ตัวแปรสุ่มแบบแยก X ซึ่งมีการแจกแจงแบบไฮเปอร์เรขาคณิตที่มีพารามิเตอร์ N=8, K=5 และ n=3 ถูกกำหนดไว้ดังนี้:
![]()
สูตรการกระจายแบบไฮเปอร์เรขาคณิต
สูตรสำหรับการแจกแจงแบบไฮเปอร์เรขาคณิต เป็นผลคูณของจำนวนเชิงรวมของ K ส่วน x ด้วยจำนวนเชิงรวมของ NK ส่วน nx หารด้วยจำนวนเชิงรวมของ N ส่วน n

โดยที่ N คือขนาดประชากร K คือจำนวนกรณีที่เป็นไปได้ทั้งหมด n คือจำนวนการแยกข้อมูลโดยไม่มีการแทนที่ และ x คือจำนวนกรณีที่น่าพอใจซึ่งต้องคำนวณความน่าจะเป็นที่จะเกิดขึ้น
👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณความน่าจะเป็นของเหตุการณ์ของตัวแปรที่เป็นไปตามการแจกแจงแบบไฮเปอร์เรขาคณิต
ตัวอย่างการกระจายตัวแบบไฮเปอร์เรขาคณิต
เมื่อเราได้เห็นคำจำกัดความและสูตรของการแจกแจงแบบไฮเปอร์เรขาคณิตแล้ว ตอนนี้เราจะแก้ตัวอย่างทีละขั้นตอนเพื่อให้คุณทราบวิธีคำนวณความน่าจะเป็นของการแจกแจงแบบไฮเปอร์เรขาคณิต
- ในถุงหนึ่งเราใส่ลูกบอลสีน้ำเงิน 20 ลูกและลูกบอลสีแดง 30 ลูก กล่าวคือ ภายในถุงมีลูกบอลทั้งหมด 50 ลูก ถ้าเราจั่วลูกบอล 12 ลูกโดยไม่เปลี่ยนลูกใดเลย จงหาความน่าจะเป็นที่จะจั่วลูกบอลสีน้ำเงิน 4 ลูก
สิ่งแรกที่เราต้องทำเพื่อแก้แบบฝึกหัดคือระบุพารามิเตอร์ของการแจกแจงแบบไฮเปอร์เรขาคณิต ในกรณีนี้ จำนวนองค์ประกอบทั้งหมดในประชากรคือ 50 ( ยังไม่มีข้อความ =50) จำนวนกรณีที่เหมาะสมสูงสุดคือ 20 ( K =20) และดึงลูกบอล 12 ลูก ( n =12)
![Rendered by QuickLaTeX.com \left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)](https://statorials.org/wp-content/ql-cache/quicklatex.com-352132f74408eab99d3985c63a49f322_l3.png)
เราต้องการคำนวณความน่าจะเป็นของการวาดลูกบอลสีน้ำเงิน 4 ลูก ( x =4) ดังนั้นเราจึงใช้สูตรการกระจายแบบไฮเปอร์เรขาคณิตแทนตัวแปรด้วยค่าที่สอดคล้องกันแล้วทำการคำนวณ:
![Rendered by QuickLaTeX.com P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-caf83b14deae0fe9882e4d40e677329f_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-ed747dd327149d4a925e6ad7c4119f81_l3.png)
เครื่องคำนวณการกระจายไฮเปอร์เรขาคณิต
ป้อนพารามิเตอร์ของการแจกแจงแบบไฮเปอร์เรขาคณิตลงในเครื่องคิดเลขออนไลน์ต่อไปนี้เพื่อคำนวณความน่าจะเป็นที่เหตุการณ์จะเกิดขึ้น
โปรดจำไว้ว่า N คือขนาดประชากร K คือจำนวนกรณีที่เป็นไปได้ทั้งหมด n คือขนาดของกลุ่มตัวอย่าง และ x คือค่าที่เราต้องการค้นหาความน่าจะเป็นของเหตุการณ์นี้
ลักษณะของการกระจายตัวแบบไฮเปอร์เรขาคณิต
การกระจายแบบไฮเปอร์เรขาคณิตมีคุณสมบัติดังต่อไปนี้:
- ค่าที่คาดหวังของการแจกแจงแบบไฮเปอร์เรขาคณิต จะเท่ากับจำนวนองค์ประกอบในกลุ่มตัวอย่างคูณด้วยจำนวนกรณีที่เป็นประโยชน์ทั้งหมดหารด้วยจำนวนองค์ประกอบในประชากร
![]()
- โหมดของการแจกแจงแบบไฮเปอร์เรขาคณิต คือค่าที่ปัดเศษลงจากผลคูณของ n+1 คูณ K+1 หารด้วย N+2
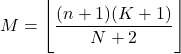
- ความแปรปรวนของการแจกแจงแบบไฮเปอร์จีโอเมตริก สามารถรับได้โดยใช้นิพจน์ต่อไปนี้:
![]()
- ฟังก์ชันการสร้างโมเมนต์ของการแจกแจงแบบไฮเปอร์เรขาคณิตจะเป็นดังนี้:
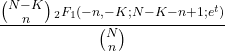
- ฟังก์ชันลักษณะเฉพาะของการแจกแจงแบบไฮเปอร์เรขาคณิตมีดังนี้:
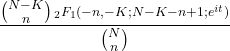
- ความน่าจะเป็นที่จะเกิดขึ้นของเหตุการณ์ตามจำนวนที่กำหนดสามารถคำนวณได้จากความน่าจะเป็นของจำนวนก่อนหน้าโดยใช้การเรียกซ้ำสำหรับการแจกแจงแบบไฮเปอร์เรขาคณิต:
![]()
การกระจายตัวแบบไฮเปอร์เรขาคณิตและการกระจายแบบทวินาม
ความแตกต่างระหว่างการกระจายแบบไฮเปอร์เรขาคณิตและการแจกแจงแบบทวินาม คือการแทนที่ การกระจายแบบไฮเปอร์เรขาคณิตจะใช้เมื่อไม่ได้แทนที่การดึงข้อมูล อย่างไรก็ตาม การดึงข้อมูลแบบทวินามจะถูกแทนที่
ตัวอย่างเช่น หากเราจั่วไพ่ห้าใบแบบสุ่มในหนึ่งสำรับ และเราต้องการคำนวณความน่าจะเป็นที่จะได้ไพ่บางใบ หากเราไม่เปลี่ยนไพ่แต่ละใบที่เราจั่ว เราต้องใช้การแจกแจงแบบไฮเปอร์เรขาคณิตเพื่อทำการคำนวณ แต่หากตอนถอดไพ่ออกเราใส่กลับคืนก่อนทำการแยกครั้งต่อไปเราต้องใช้การแจกแจงแบบทวินามเพื่อคำนวณความน่าจะเป็น
เมื่อตัวเลข N มีขนาดใหญ่ อัตราส่วน n/N น้อย และจำนวนกรณีที่ต้องการที่ต้องการมีน้อยมาก เราสามารถใช้การแจกแจงแบบไฮเปอร์เรขาคณิตเป็นการประมาณของการแจกแจงแบบทวินาม อย่างไรก็ตาม ฉันไม่แนะนำเพราะผลลัพธ์จะไม่น่าเชื่อถือเท่าที่ควร และยิ่งไปกว่านั้น การคำนวณความน่าจะเป็นด้วยกฎทวินามได้ง่ายกว่ากฎไฮเปอร์จีโอเมตริก