ความรู้เบื้องต้นเกี่ยวกับการกระจายตัวทางเรขาคณิต

การกระจายทางเรขาคณิต อธิบายถึงความน่าจะเป็นที่จะประสบความล้มเหลวจำนวนหนึ่งก่อนที่จะประสบความสำเร็จครั้งแรกในการทดลองแบบเบอร์นูลลีหลายครั้ง

การทดลองแบบเบอร์นูลลี เป็นการทดลองที่มีผลลัพธ์ที่เป็นไปได้เพียงสองผลลัพธ์เท่านั้น ได้แก่ “ความสำเร็จ” หรือ “ความล้มเหลว” และความน่าจะเป็นที่จะประสบความสำเร็จจะเท่ากันทุกครั้งที่ทำการทดลอง

ตัวอย่างของเรียงความของ Bernoulli คือการโยนเหรียญ เหรียญสามารถลงได้สองหัวเท่านั้น (เราอาจเรียกหัวว่า “ตี” และก้อยว่า “ล้มเหลว”) และความน่าจะเป็นที่จะสำเร็จในการพลิกแต่ละครั้งคือ 0.5 โดยถือว่าเหรียญนั้นยุติธรรม

ถ้า ตัวแปรสุ่ม X เป็นไปตามการแจกแจงทางเรขาคณิต ความน่าจะเป็นที่จะประสบความล้มเหลว k ก่อนที่จะประสบความสำเร็จครั้งแรกสามารถหาได้จากสูตรต่อไปนี้:

P(X=k) = (1-p) ^kp

ทอง:

• k: จำนวนความล้มเหลวก่อนความสำเร็จครั้งแรก
• p: ความน่าจะเป็นที่จะประสบความสำเร็จในแต่ละการทดลอง

ตัวอย่างเช่น สมมติว่าเราต้องการทราบว่าเราต้องพลิกเหรียญยุติธรรมกี่ครั้งจนกว่าเหรียญจะขึ้นหัว เราสามารถใช้สูตรด้านบนเพื่อกำหนดความน่าจะเป็นที่จะประสบความล้มเหลว 0, 1, 2, 3 เป็นต้น ก่อนที่เหรียญจะตกใส่หัว:

หมายเหตุ: เหรียญสามารถประสบกับ “ความล้มเหลว” 0 ถ้ามันเกิดขึ้นในการโยนครั้งแรก

P(X=0) = (1-.5) ⁰ (.5) = 0.5

P(X=1) = (1-.5) ¹ (.5) = 0.25

P(X=2) = (1-.5) ² (.5) = 0.125

ป(X=3) = (1-0.5) ³ (0.5) = 0.0625

เราสามารถคำนวณความน่าจะเป็นของการโยนเหรียญจำนวนเท่าใดก็ได้จนถึงอนันต์ จากนั้นเราจะสร้างฮิสโตแกรมอย่างง่ายเพื่อแสดงภาพการแจกแจงความน่าจะเป็น:

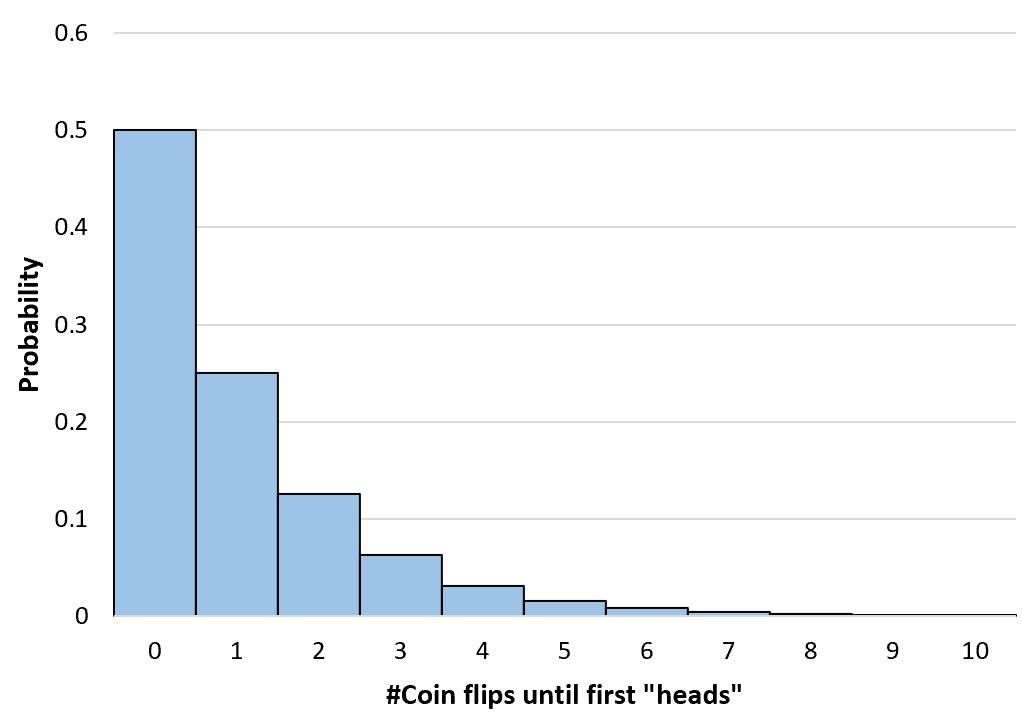
การคำนวณความน่าจะเป็นทางเรขาคณิตสะสม

ความน่าจะเป็นสะสม ที่เราพบความล้มเหลว k หรือน้อยกว่าจนกระทั่งประสบความสำเร็จครั้งแรกสามารถพบได้ โดยสูตรต่อไปนี้:

P(X≤k) = 1 – (1-p) ^k+1

ทอง:

• k: จำนวนความล้มเหลวก่อนความสำเร็จครั้งแรก
• p: ความน่าจะเป็นที่จะประสบความสำเร็จในแต่ละการทดลอง

ตัวอย่างเช่น สมมติว่าเราต้องการทราบความน่าจะเป็นที่เหรียญจะ “พลาด” สามครั้งหรือน้อยกว่านั้นก่อนที่เหรียญจะตกหัวในที่สุด เราจะใช้สูตรต่อไปนี้เพื่อคำนวณความน่าจะเป็นนี้:

P(X≤3) = 1 – (1-0.5) ³⁺¹ = 0.9375

เราสามารถคำนวณความน่าจะเป็นสะสมแต่ละรายการได้โดยใช้สูตรที่คล้ายกัน:

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0.5

P(X≤1) = 1 – (1-0.5) ¹⁺¹ = 0.75

P(X≤2) = 1 – (1-0.5) ²⁺¹ = 0.875

เราสามารถคำนวณความน่าจะเป็นสะสมเหล่านี้สำหรับการโยนเหรียญจำนวนเท่าใดก็ได้จนถึงอนันต์ จากนั้นเราสามารถสร้างฮิสโตแกรมเพื่อแสดงภาพการแจกแจงความน่าจะเป็นสะสมได้:

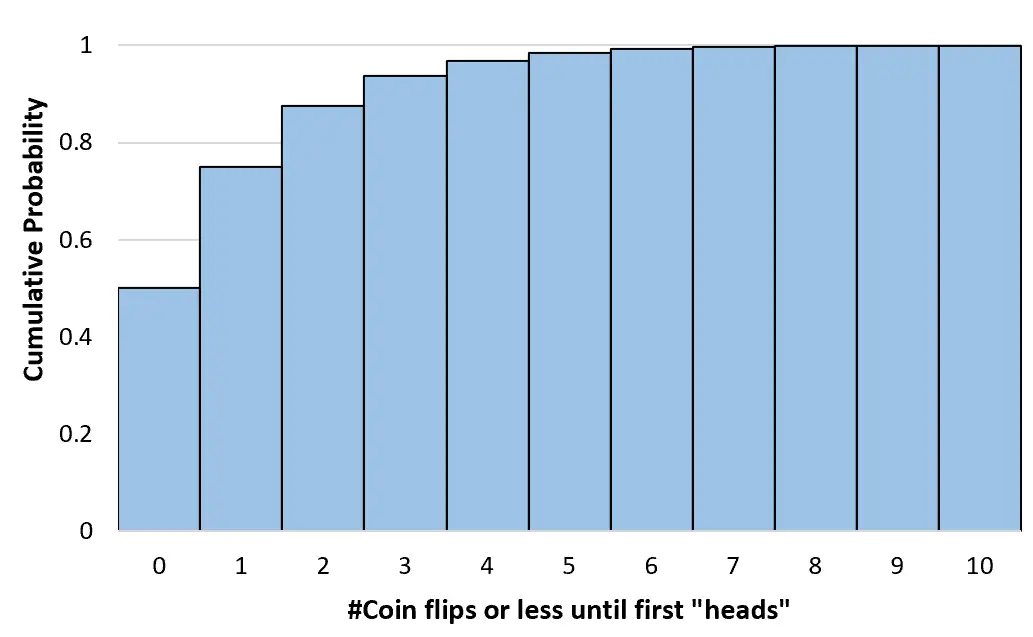
คุณสมบัติของการกระจายตัวทางเรขาคณิต

การกระจายทางเรขาคณิตมีคุณสมบัติดังต่อไปนี้:

ค่าเฉลี่ยของการแจกแจงคือ (1-p) / p

ความแปรปรวนของการแจกแจงคือ (1-p) / p ²

ตัวอย่างเช่น:

จำนวนครั้งโดยเฉลี่ยที่เราคาดว่าเหรียญจะออกหัวก่อนจะออกก้อยคือ (1-p) / p = (1-.5) / .5 = 1

ความแปรปรวนของจำนวนการทอยจนกระทั่งตกหัวจะเป็น (1-p)/ ^p2 =(1-.5)/ ⁵² = 2 .

ปัญหาการฝึกแจกแจงทางเรขาคณิต

ใช้แบบฝึกหัดแก้ปัญหาต่อไปนี้เพื่อทดสอบความรู้เรื่องการแจกแจงทางเรขาคณิต

หมายเหตุ: เราจะใช้ เครื่องคำนวณการกระจายทางเรขาคณิต เพื่อคำนวณคำตอบสำหรับคำถามเหล่านี้

ปัญหาที่ 1

คำถาม: นักวิจัยรออยู่ด้านนอกห้องสมุดเพื่อถามผู้คนว่าพวกเขาสนับสนุนกฎหมายบางข้อหรือไม่ ความน่าจะเป็นที่บุคคลหนึ่งสนับสนุนกฎหมายคือ p = 0.2 ความน่าจะเป็นที่บุคคลที่สี่ที่ผู้วิจัยพูดด้วยจะเป็นคนแรกที่สนับสนุนกฎหมายคือเท่าใด

คำตอบ: จำนวน “ความล้มเหลว” จนถึงความสำเร็จครั้งแรก นั่นคือจำนวนคนที่ไม่สนับสนุนกฎหมายจนกว่าคนแรกจะสนับสนุน คือ 3 ดังนั้น ในการใช้เครื่องคำนวณการกระจายตัวทางเรขาคณิตโดยมีค่า p = 0.2 และ x = ความล้มเหลว 3 ครั้ง เราพบว่า P(X=3) = 0.10240

ปัญหาที่ 2

คำถาม: นักวิจัยรออยู่ด้านนอกห้องสมุดเพื่อถามผู้คนว่าพวกเขาสนับสนุนกฎหมายบางข้อหรือไม่ ความน่าจะเป็นที่บุคคลหนึ่งสนับสนุนกฎหมายคือ p = 0.2 ความน่าจะเป็นที่ผู้วิจัยจะต้องพูดคุยกับคน มากกว่า สี่คนจึงจะหาคนที่สนับสนุนกฎหมายเป็นเท่าใด

คำตอบ: เมื่อใช้เครื่องคำนวณการกระจายตัวทางเรขาคณิตที่มีความล้มเหลว p =0.2 และ x = 4 เราพบว่า P(X>4) = 0.32768

ปัญหา 3

คำถาม: นักวิจัยรออยู่ด้านนอกห้องสมุดเพื่อถามผู้คนว่าพวกเขาสนับสนุนกฎหมายบางข้อหรือไม่ ความน่าจะเป็นที่บุคคลหนึ่งสนับสนุนกฎหมายคือ p = 0.2 ผู้วิจัยจะต้องพูดคุยด้วยด้วยจำนวนคนที่คาดหวังไว้เป็นจำนวนเท่าใดจนกว่าเธอจะพบคนที่สนับสนุนกฎหมาย

คำตอบ: จำไว้ว่าค่าเฉลี่ยของการแจกแจงทางเรขาคณิตคือ (1-p) / p ในสถานการณ์นี้ ค่าเฉลี่ยจะเป็น (1-.2) / .2 = 4