การกระจายตัวแบบปกติมาตรฐาน

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 4, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจงแบบปกติมาตรฐานคืออะไร และใช้เพื่ออะไร นอกจากนี้คุณยังจะพบคุณสมบัติของการแจกแจงแบบปกติมาตรฐาน ตารางที่มีค่าคุณลักษณะและแบบฝึกหัดที่แก้ไขเพิ่มเติมอีกด้วย

การแจกแจงแบบปกติมาตรฐานคืออะไร?

การแจกแจงแบบปกติมาตรฐาน หรือที่เรียกว่า การแจกแจงแบบปกติแบบหน่วย เป็นกรณีที่ง่ายที่สุดของการแจกแจงแบบปกติ แม่นยำยิ่งขึ้นการแจกแจงแบบปกติมาตรฐานคือการแจกแจงแบบปกติที่มีค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานเท่ากับ 0 และ 1 ตามลำดับ

ดังนั้น การแจกแจงแบบปกติมาตรฐานจึงถูกกำหนดเป็น N(0,1) โดยที่พารามิเตอร์ตัวแรกคือค่าเฉลี่ยของการแจกแจง และพารามิเตอร์ตัวที่สองคือค่าเบี่ยงเบนมาตรฐาน (หรือ SD)

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

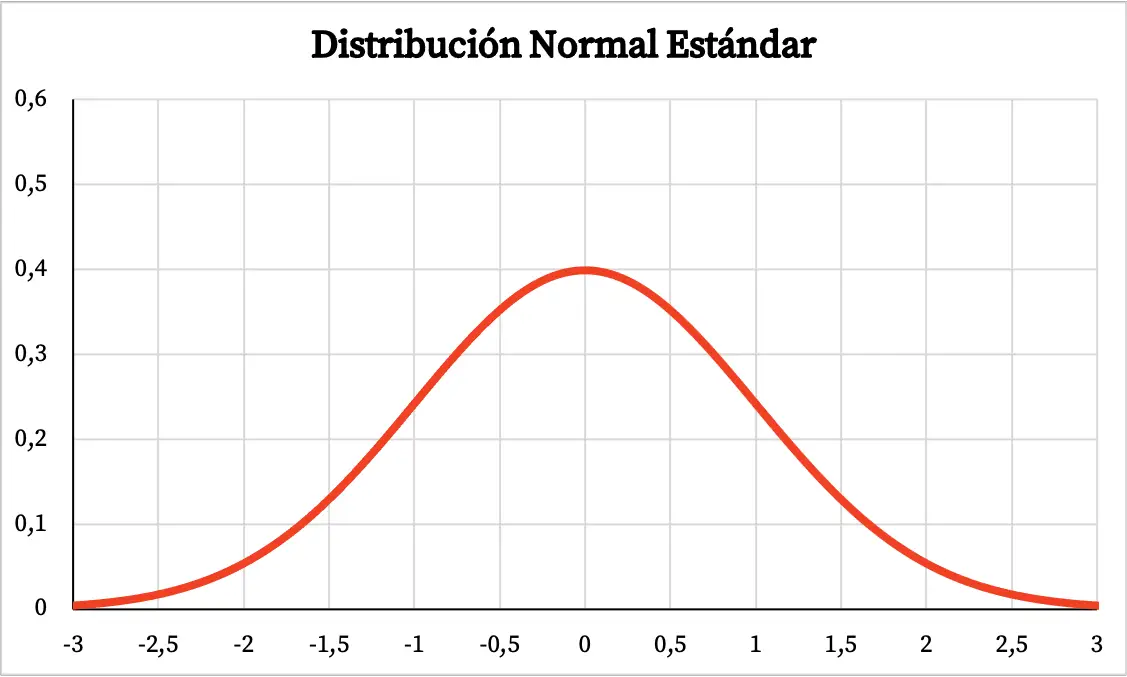
กราฟของการแจกแจงแบบปกติมาตรฐานจึงเป็นดังนี้:

สูตรสำหรับการแจกแจงแบบปกติมาตรฐาน

ในการแปลงการแจกแจงแบบปกติใดๆ ให้เป็นการแจกแจงแบบปกติมาตรฐาน คุณต้องลบค่าเฉลี่ยของการแจกแจงแบบปกติออกจากค่าทั้งหมด แล้วหารด้วยค่าเบี่ยงเบนมาตรฐานของการแจกแจงแบบปกติ

สูตรสำหรับการแจกแจงแบบปกติมาตรฐาน จึงเป็นดังนี้:

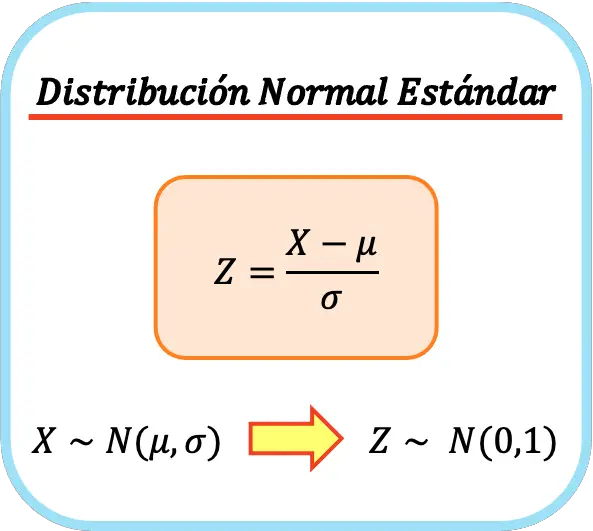
ด้วยวิธีนี้ ค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานของตัวแปรใหม่จะเป็น 0 และ 1 ตามลำดับ ดังนั้น เราจะได้การแจกแจงแบบปกติมาตรฐาน กระบวนการนี้เรียกอีกอย่างว่า การทำให้เป็นมาตรฐานแบบตัวแปรเดียว หรือ การทำให้เป็นมาตรฐานแบบตัวแปรเดียว

ตารางการแจกแจงแบบปกติมาตรฐาน

ตารางการแจกแจงแบบปกติมาตรฐานคือตารางที่มีความน่าจะเป็นที่ค่าที่สังเกตได้น้อยกว่าค่าที่กำหนดของการแจกแจงแบบปกติมาตรฐาน

นอกจากนี้ เนื่องจากฟังก์ชันของการแจกแจงแบบปกติขึ้นอยู่กับค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐาน ตารางการแจกแจงแบบปกติมาตรฐานจึงถูกนำมาใช้เพื่อระบุความน่าจะเป็นของการแจกแจงแบบปกติด้วย เมื่อต้องการทำเช่นนี้ การแจกแจงแบบปกติจะถูกพิมพ์ลงในการแจกแจงแบบปกติมาตรฐาน จากนั้นเราจะดูในตารางว่าความน่าจะเป็นที่สอดคล้องกับการแจกแจงแบบปกตินั้นเป็นอย่างไร

ดังนั้นค่าในตารางการแจกแจงแบบปกติมาตรฐานจึงเป็นดังนี้:

ตัวอย่างของการแจกแจงแบบปกติมาตรฐาน

ตอนนี้เรารู้คำจำกัดความของการแจกแจงแบบปกติมาตรฐานและสูตรของมันแล้ว ต่อไปนี้เป็นตัวอย่างที่เป็นรูปธรรมเพื่อทำความเข้าใจแนวคิดนี้ให้ดี

ตัวแปรสุ่มต่อเนื่องเป็นไปตามการแจกแจงแบบปกติโดยมีค่าเฉลี่ย 45 และส่วนเบี่ยงเบนมาตรฐาน 15 ความน่าจะเป็นที่จะได้ค่าน้อยกว่าหรือเท่ากับ 58 เป็นเท่าใด

$N(45,15)\ \color{orange}\bm{\longrightarrow}\color{black}\ P[X\leq 58]= \ \color{orange}\bm{?}\color{black}$

ในการค้นหาความน่าจะเป็นของการแจกแจงแบบปกติ เราจำเป็นต้องใช้ตารางคุณลักษณะของมัน แต่ในการทำเช่นนั้น เราต้องดำเนินการพิมพ์ก่อนเพื่อให้ได้การแจกแจงแบบปกติมาตรฐาน เราจึงใช้สูตรการแจกแจงแบบปกติมาตรฐาน:

$Z=\cfrac{X-\mu}{\sigma}$

เราก็ลบค่าเฉลี่ยออกจากค่าความน่าจะเป็น แล้วหารด้วยค่าเบี่ยงเบนมาตรฐาน

$\displaystyle P[X\leq 58]=P\left[Z\leq\frac{58-45}{15}\right]=P[Z\leq 0,87]$

เมื่อเรากำหนดตัวแปรให้เป็นมาตรฐานแล้ว เราจะไปที่ตารางความน่าจะเป็นของการแจกแจงแบบปกติมาตรฐาน (ดูด้านบน) เพื่อดูว่าค่าความน่าจะเป็นของ 0.87 สอดคล้องกับค่าใด:

$\displaystyle P[Z\leq 0,87]=0,8078$

ความน่าจะเป็นที่จะได้ค่าเท่ากับหรือน้อยกว่า 58 จึงเป็น 80.78%

ลักษณะของการแจกแจงแบบปกติมาตรฐาน

การแจกแจงแบบปกติมาตรฐานมีลักษณะดังต่อไปนี้:

การแจกแจงแบบปกติมาตรฐานคือการแจกแจงแบบสมมาตรที่มีศูนย์กลางอยู่ที่ 0
เช่นเดียวกับการแจกแจงแบบปกติ กราฟการแจกแจงแบบปกติมาตรฐานจะมีรูปทรงระฆัง โดยพื้นที่กราฟส่วนใหญ่จะอยู่รอบๆ ค่าเฉลี่ย
ดังนั้น ค่าเฉลี่ย รูปแบบ และค่ามัธยฐานของการแจกแจงแบบปกติจะมีค่าเท่ากัน ซึ่งก็คือ 0
การแจกแจงแบบปกติมาตรฐานจะมีค่าสูงสุดที่ z=0
ในทำนองเดียวกัน การแจกแจงแบบปกติมาตรฐานจะมีจุดเปลี่ยนเว้าสองจุด ที่ z=-1 และ z=+1
ตามกฎทั่วไป เรารู้ว่า 68% ของค่าอยู่ในการแจกแจงแบบปกติมาตรฐานระหว่าง +1 ถึง -1, 95% ของค่าระหว่าง +2 ถึง -2 ถึง 99.7% ของค่าระหว่าง + 3 และ – 3

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม