การกระจายเบต้า
บทความนี้จะอธิบายว่าการแจกแจงแบบเบต้าคืออะไรและใช้เพื่ออะไร ในทำนองเดียวกัน คุณจะเห็นกราฟการแจกแจงแบบเบต้าและคุณสมบัติของการแจกแจงความน่าจะเป็นประเภทนี้
การกระจายเบต้าคืออะไร?
การแจกแจงแบบเบต้า คือการแจกแจงความน่าจะเป็นที่กำหนดในช่วงเวลา (0,1) และกำหนดพารามิเตอร์ด้วยพารามิเตอร์บวกสองตัว: α และ β กล่าวอีกนัยหนึ่งค่าของการแจกแจงเบต้าขึ้นอยู่กับพารามิเตอร์αและβ
ดังนั้น คุณสมบัติหลักของการแจกแจงแบบเบต้าคือสามารถควบคุมรูปร่างได้ด้วยพารามิเตอร์ α และ β นอกจากนี้ การแจกแจงแบบเบต้ายังใช้เพื่อกำหนดตัวแปรสุ่มที่มีค่าอยู่ระหว่าง 0 ถึง 1
มีสัญลักษณ์หลายประการที่บ่งชี้ว่าตัวแปรสุ่มต่อเนื่องถูกควบคุมโดยการแจกแจงแบบเบต้า ลักษณะที่พบบ่อยที่สุดคือ:
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-ee1d0d8a1624a017b8ef9ce8a67c694e_l3.png)
ตามสถิติแล้ว การแจกแจงแบบเบต้ามีการใช้งานที่หลากหลายมาก ตัวอย่างเช่น การแจกแจงแบบเบต้าใช้เพื่อศึกษาความแปรผันของเปอร์เซ็นต์ในกลุ่มตัวอย่างต่างๆ ในทำนองเดียวกัน ในการจัดการโครงการ การกระจายเบต้าจะใช้เพื่อทำการวิเคราะห์ Pert
แผนการกระจายเบต้า
เมื่อพิจารณาถึงคำจำกัดความของการแจกแจงแบบเบต้า ฟังก์ชันความหนาแน่นและฟังก์ชันการแจกแจงความน่าจะเป็นของการแจกแจงแบบเบต้าจะแสดงไว้ด้านล่าง
ด้านล่างนี้ คุณจะเห็นว่ากราฟฟังก์ชันความหนาแน่นของการแจกแจงแบบเบต้าแตกต่างกันอย่างไร โดยขึ้นอยู่กับพารามิเตอร์ α และ β
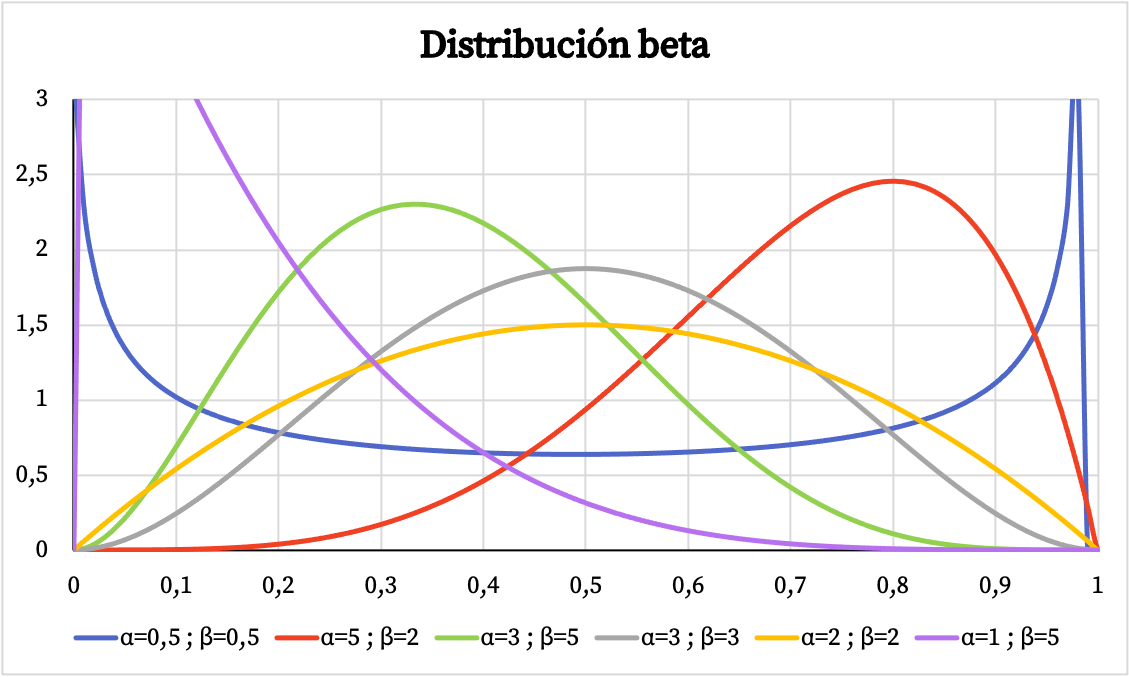
ในทำนองเดียวกัน ด้านล่างคุณจะเห็นการแสดงกราฟิกของความน่าจะเป็นสะสมของการแจกแจงแบบเบต้าโดยอิงตามพารามิเตอร์ α และ β
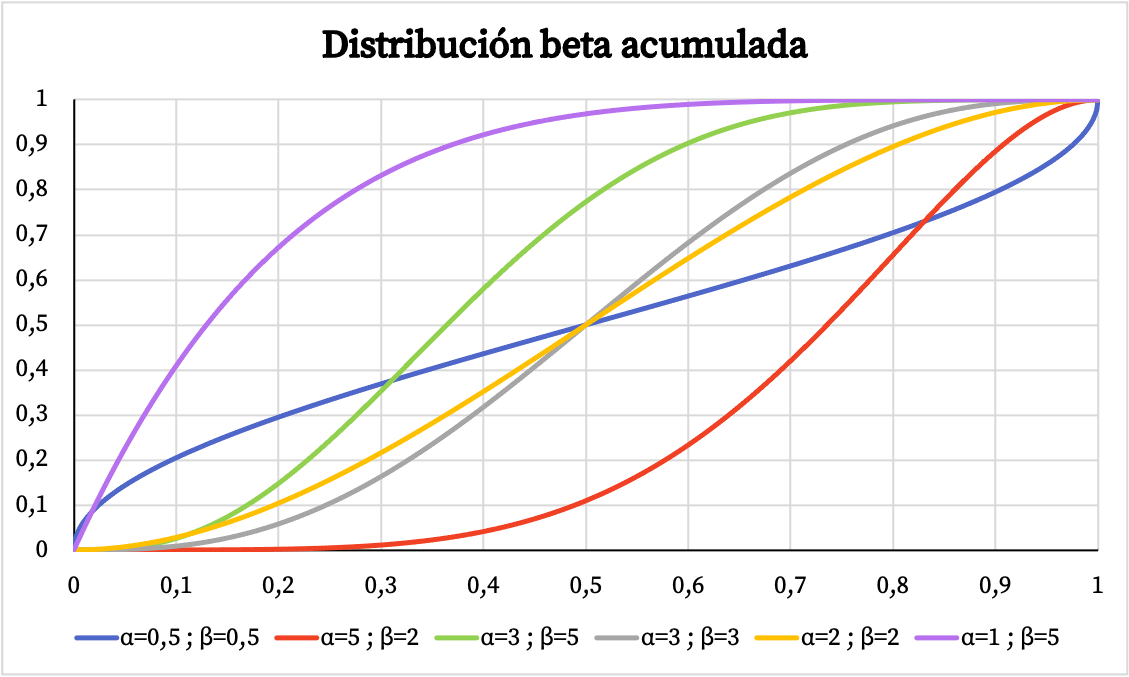
ลักษณะของการกระจายเบต้า
ในส่วนนี้เราจะดูว่าคุณลักษณะที่สำคัญที่สุดของการแจกแจงแบบเบต้าคืออะไร
- พารามิเตอร์ α และ β ของการแจกแจงแบบเบต้าเป็นจำนวนจริงและจำนวนบวก
![\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”44″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> โดเมนของการแจกแจงแบบเบต้ามีตั้งแต่ 0 ถึง 1 โดยไม่รวมค่าสุดขั้วทั้งสอง</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-442bebaba847543d6db71cdf0127a4b0_l3.png)
![]()
- ค่าเฉลี่ยของการแจกแจงแบบเบตาเท่ากับอัลฟาหารด้วยผลรวมอัลฟ่าบวกเบตา
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4530a8b72211111e8bec79b6388e00a7_l3.png)
- ความแปรปรวนของการแจกแจงแบบเบต้าสามารถคำนวณได้โดยใช้สูตรต่อไปนี้:
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-71c6ef40db833722e63c56cd763d6601_l3.png)
- สำหรับค่าอัลฟ่าและเบต้าที่มากกว่า 1 คุณสามารถค้นหาโหมดการกระจายเบต้าได้อย่างง่ายดายด้วยนิพจน์ต่อไปนี้:
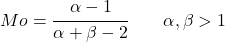
![]()
โดยที่ B(α,β) คือฟังก์ชันเบต้า ซึ่งกำหนดเป็น:
![]()
- ฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบเบต้าคือ:
![]()
โดยที่ B(x;α,β) คือฟังก์ชันเบต้าที่ไม่สมบูรณ์ ซึ่งกำหนดเป็น:
![]()
- ถ้า X เป็นตัวแปรที่กำหนดโดยการแจกแจงแบบเบต้า ดังนั้น 1-X จะเป็นตัวแปรที่กำหนดโดยการแจกแจงแบบเบต้าโดยที่พารามิเตอร์อัลฟ่าและเบต้าคือพารามิเตอร์เบต้าและอัลฟ่าของการแจกแจงแบบเบต้าดั้งเดิม ตามลำดับ
![]()
- หากพารามิเตอร์อัลฟ่าและเบต้าของการแจกแจงแบบเบต้ามีค่าเท่ากับ 1 ทั้งคู่ การแจกแจงจะเทียบเท่ากับการแจกแจงแบบสม่ำเสมอของพารามิเตอร์ 0 และ 1
![]()