การกระจายแบบ unimodal คืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)

การแจกแจงแบบ Unimodal คือการแจกแจงความน่าจะเป็นที่มีจุดสูงสุดที่ชัดเจน

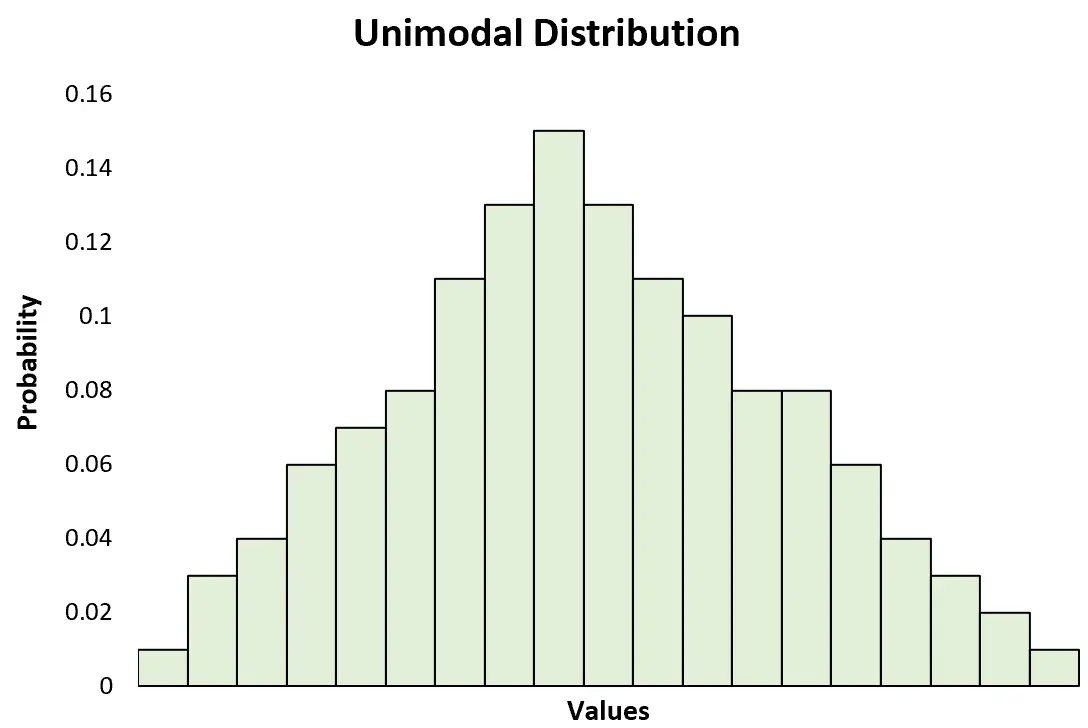
สิ่งนี้แตกต่างกับ การแจกแจงแบบไบโมดัล ซึ่งมีจุดสูงสุดที่ชัดเจนสองจุด:

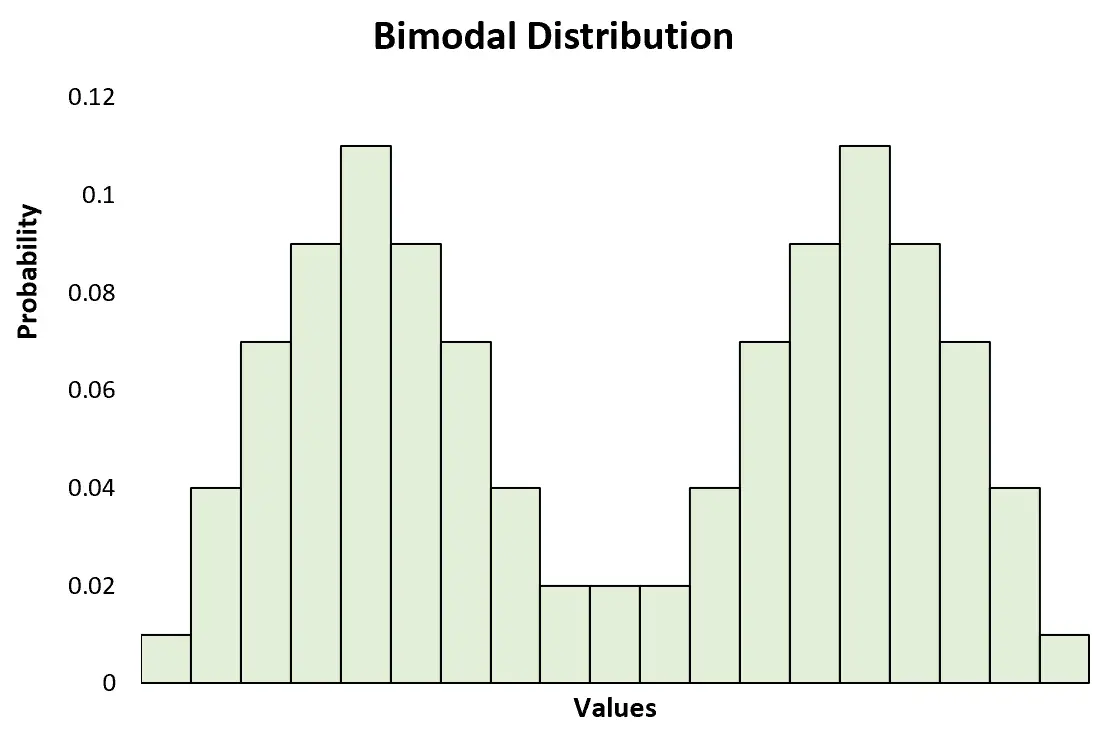
สิ่งนี้ยังแตกต่างกับ การแจกแจงแบบหลายรูปแบบ ซึ่งมียอดสองค่าขึ้นไป:

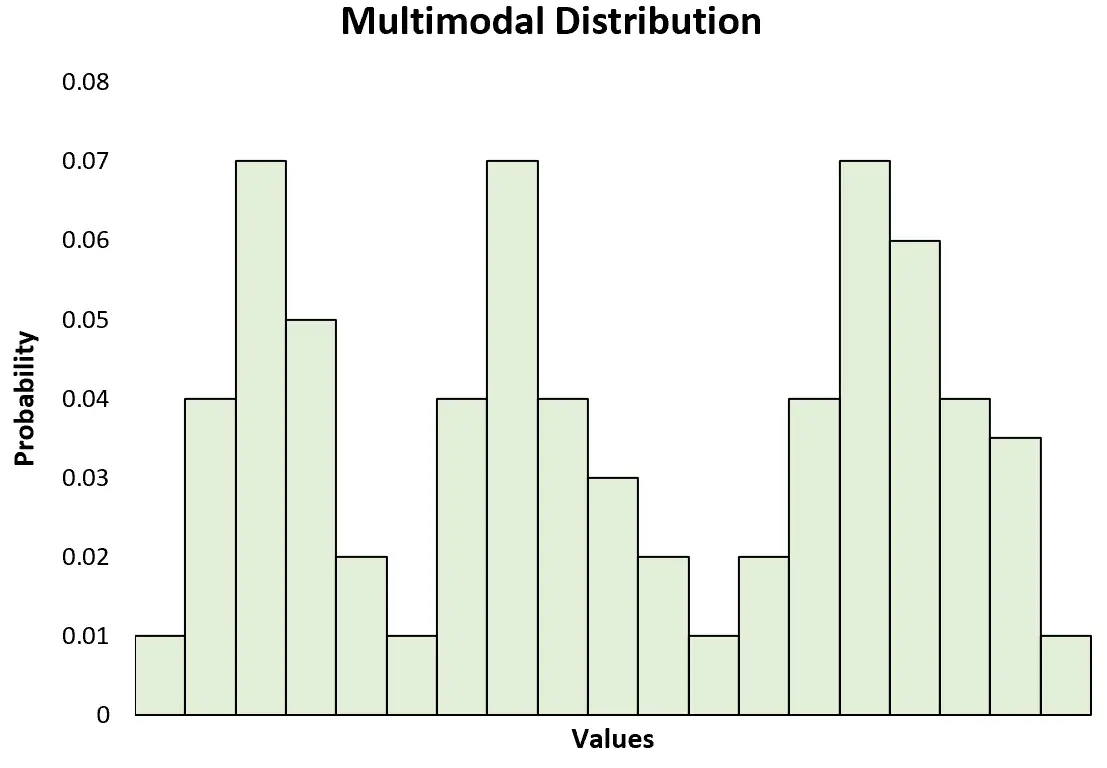
หมายเหตุ: การแจกแจงแบบไบโมดัลเป็นเพียงการแจกแจงแบบหลายรูปแบบที่เฉพาะเจาะจงเท่านั้น

ตัวอย่างของการแจกแจงแบบ Unimodal

นี่คือตัวอย่างบางส่วนของการแจกแจงแบบ Unimodal ในทางปฏิบัติ

ตัวอย่างที่ 1: น้ำหนักแรกเกิดของทารก

เป็นที่ทราบกันดีว่าการกระจายน้ำหนักของทารกแรกเกิดเป็นไปตามการกระจายแบบ Unimodal โดยมีน้ำหนักเฉลี่ยประมาณ 7.5 ปอนด์ หากเราสร้างฮิสโตแกรมของน้ำหนักทารก เราจะเห็น “จุดสูงสุด” ที่ 7.5 ปอนด์ โดยทารกบางคนมีน้ำหนักมากกว่าและบางตัวมีน้ำหนักน้อยกว่า

ตัวอย่างที่ 2: คะแนน ACT

คะแนน ACT เฉลี่ยสำหรับนักเรียนมัธยมปลายในสหรัฐอเมริกาอยู่ที่ประมาณ 21 คะแนน โดยนักเรียนบางคนทำคะแนนได้ต่ำกว่าและคนอื่นๆ ทำคะแนนได้สูงกว่า หากเราสร้างฮิสโตแกรมของคะแนน ACT สำหรับนักเรียนทุกคนในสหรัฐอเมริกา เราจะเห็น “จุดสูงสุด” เดี่ยวๆ เมื่ออายุ 21 ปี โดยมีคะแนนสูงกว่าสำหรับนักเรียนบางคนและคะแนนต่ำกว่าสำหรับคนอื่นๆ

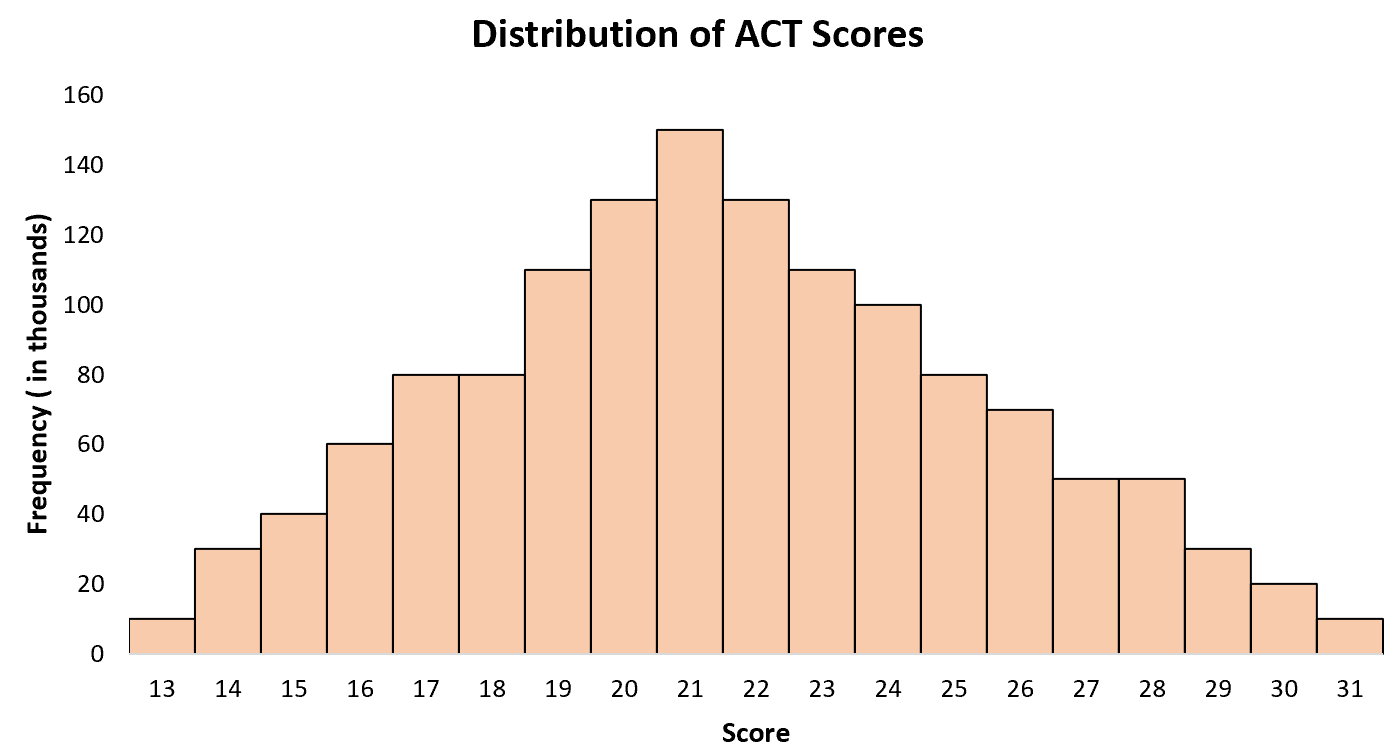
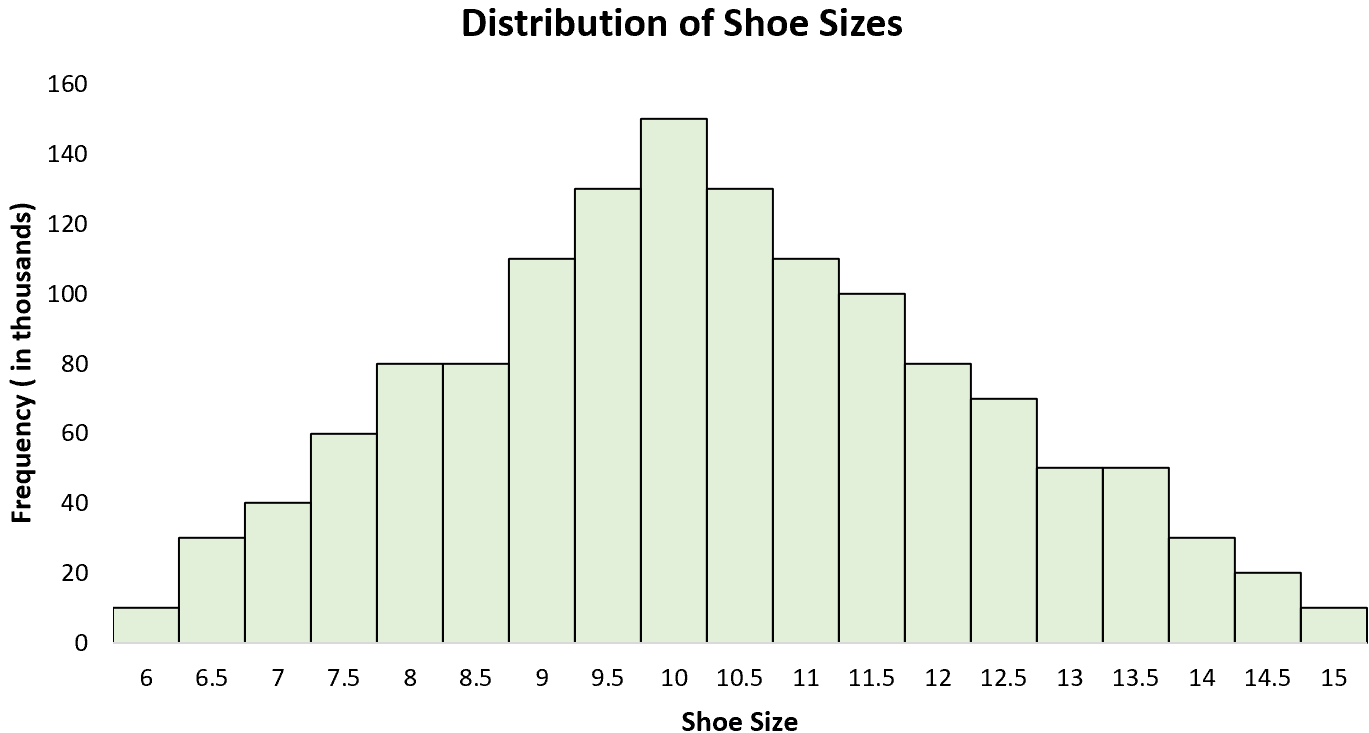
ตัวอย่างที่ 3: ขนาดรองเท้า

การกระจายขนาดรองเท้าของผู้ชายเป็นแบบกระจายแบบ Unimodal โดยมี “จุดสูงสุด” ประมาณ 10 ถ้าเราสร้างฮิสโตแกรมของขนาดรองเท้าผู้ชายทั้งหมด เราจะเห็นจุดสูงสุดเดียวที่ 10 โดยผู้ชายบางคนใส่รองเท้าไซส์ใหญ่กว่านี้ และคนอื่นๆ ใส่ขนาดรองเท้าที่ใหญ่กว่า ขนาด. ขนาดที่เล็กกว่า

การแจกแจงแบบ Unimodal ในสถิติ

การแจกแจงความน่าจะเป็นต่อไปนี้ในสถิติเป็นการแจกแจงแบบ Unimodal ทั้งหมด:

การกระจายตัวแบบปกติ

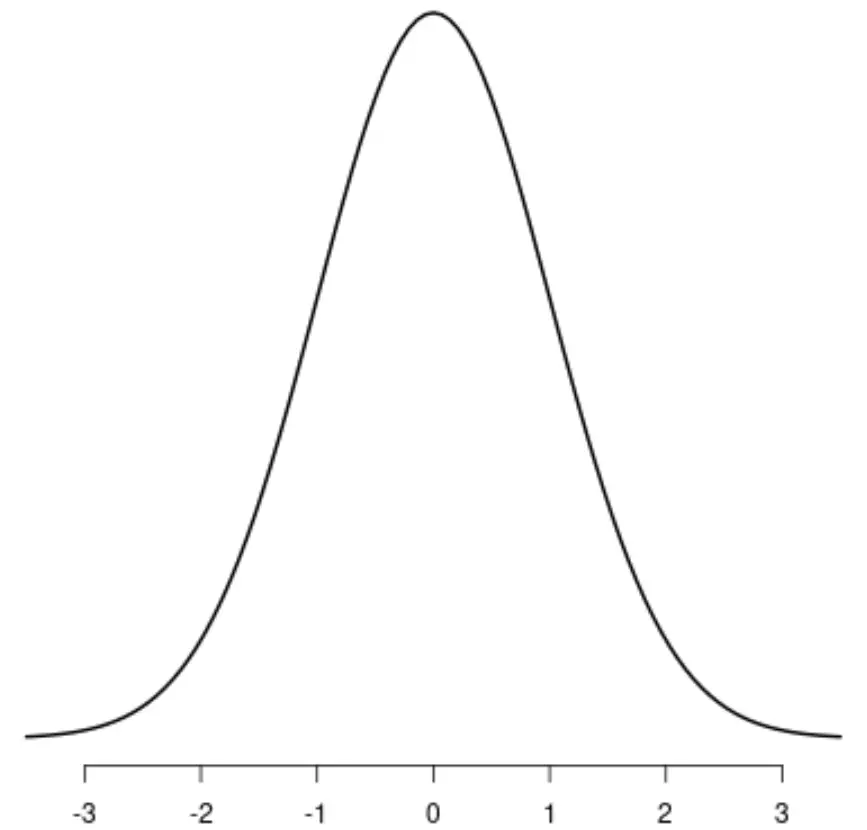
การกระจายตัวของที

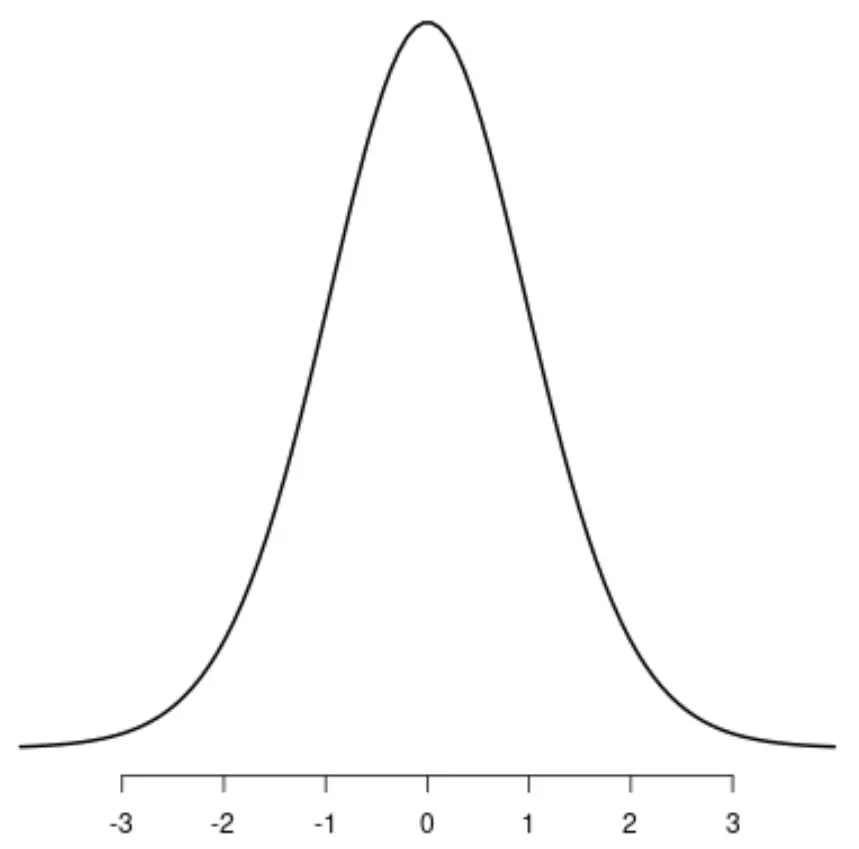
กระจายสม่ำเสมอ

การกระจายตัวของคอชี

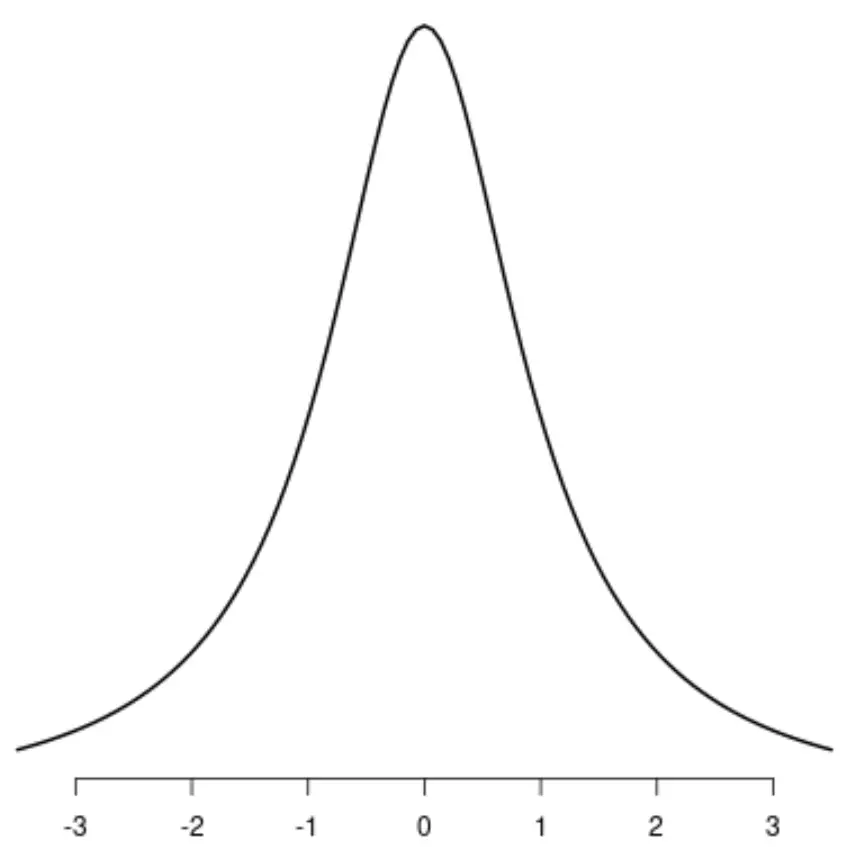
โปรดทราบว่าการแจกแจงแต่ละครั้งมีจุดสูงสุดที่แตกต่างกันเพียงจุดเดียว

วิธีการวิเคราะห์การแจกแจงแบบ Unimodal

เรามักจะอธิบายการแจกแจงแบบ Unimodal โดยใช้ การวัดแนวโน้มศูนย์กลางที่แตกต่างกัน สามแบบ:

• ค่า เฉลี่ย : ค่าเฉลี่ย
• ค่า มัธยฐาน : ค่ามัธยฐาน
• Mode : ค่าที่ปรากฏบ่อยที่สุด

ขึ้นอยู่กับ ความไม่สมมาตร ของการกระจาย การวัดทั้งสามนี้สามารถพบได้ในที่ต่างๆ

การกระจายแบบเบ้ซ้าย: ค่าเฉลี่ย < ค่ามัธยฐาน < โหมด

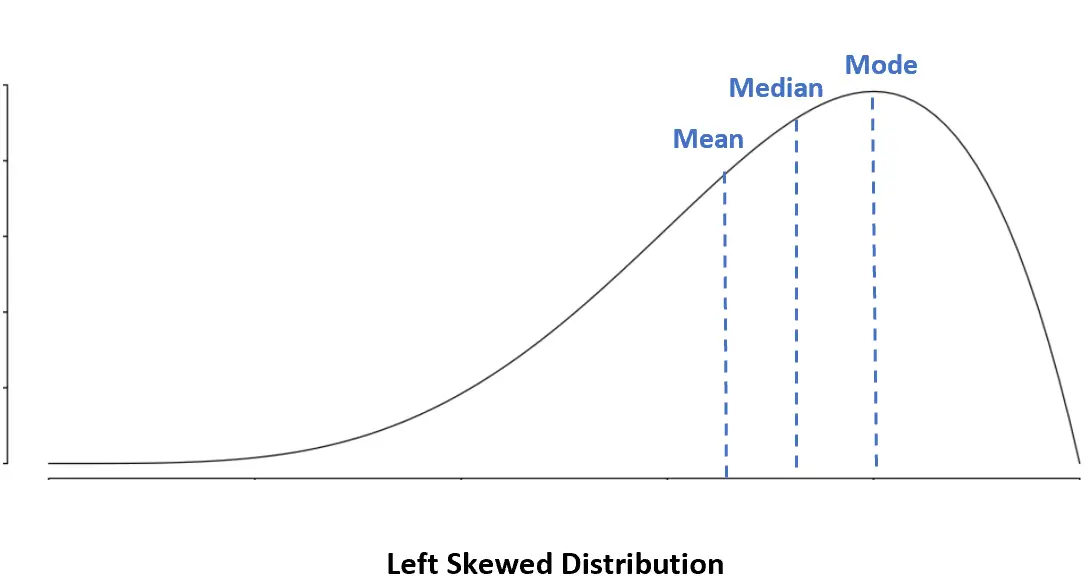
ในการแจกแจงแบบเบ้ซ้าย ค่าเฉลี่ยจะน้อยกว่าค่ามัธยฐาน

การกระจายแบบเบ้ขวา: โหมด < ค่ามัธยฐาน < ค่าเฉลี่ย

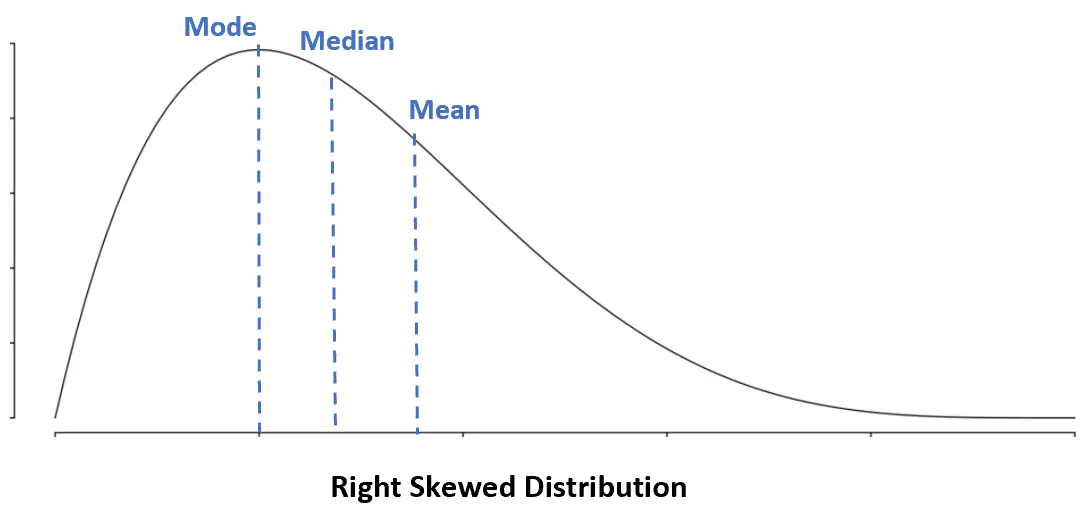
ในการแจกแจงแบบเบ้ขวา ค่าเฉลี่ยจะมากกว่าค่ามัธยฐาน

ไม่มีอคติ: ค่าเฉลี่ย = ค่ามัธยฐาน = โหมด

ในการแจกแจงแบบสมมาตร ค่าเฉลี่ย ค่ามัธยฐาน และโหมดมีค่าเท่ากัน

แหล่งข้อมูลเพิ่มเติม

การแจกแจงเบ้ซ้ายหรือขวา
การแจกแจงแบบสมมาตร: คำจำกัดความ + ตัวอย่าง