วิธีการดำเนินการถดถอยที่แข็งแกร่งใน r (ทีละขั้นตอน)

การถดถอยแบบแข็งแกร่ง เป็นวิธีการที่เราสามารถใช้เป็นทางเลือกแทนการถดถอยกำลังสองน้อยที่สุดแบบธรรมดา เมื่อมีค่าผิดปกติหรือ ข้อสังเกตที่มีอิทธิพล ในชุดข้อมูลที่เรากำลังดำเนินการอยู่

เพื่อทำการถดถอยแบบแข็งแกร่งใน R เราสามารถใช้ฟังก์ชัน rlm() จากแพ็คเกจ MASS ซึ่งใช้ไวยากรณ์ต่อไปนี้:

ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีการถดถอยแบบแข็งแกร่งใน R สำหรับชุดข้อมูลที่กำหนด

ขั้นตอนที่ 1: สร้างข้อมูล

ขั้นแรก เรามาสร้างชุดข้อมูลปลอมเพื่อใช้งานกับ:

 #create data
df <- data. frame (x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2 y
1 1 7 17
2 3 7 170
3 3 4 19
4 4 29 194
5 4 13 24
6 6 34 2

ขั้นตอนที่ 2: ดำเนินการถดถอยกำลังสองน้อยสุดสามัญ

ต่อไป เรามาประกอบแบบจำลองการถดถอยกำลังสองน้อยที่สุดธรรมดาและสร้างพล็อตของ ค่าคงเหลือที่เป็นมาตรฐาน

ในทางปฏิบัติ เรามักจะพิจารณาปริมาณคงเหลือที่เป็นมาตรฐานใดๆ ซึ่งมีค่าสัมบูรณ์มากกว่า 3 ว่าเป็นค่าผิดปกติ

 #fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab=' Standardized Residuals ', xlab=' y ') 
abline(h= 0 ) 

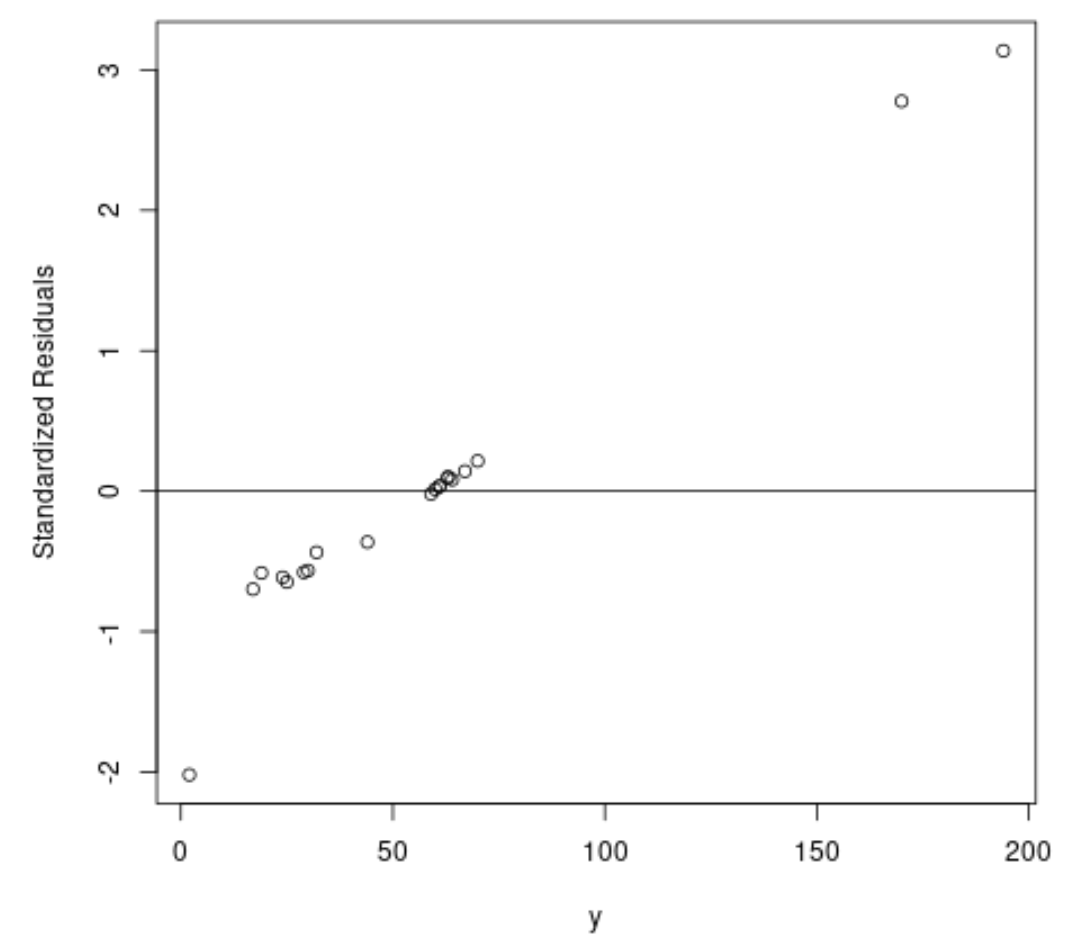
จากกราฟเราจะเห็นว่ามีการสังเกต 2 รายการโดยมีปริมาณคงเหลือมาตรฐานประมาณ 3

สิ่งนี้บ่งชี้ว่าชุดข้อมูลอาจมีค่าผิดปกติสองค่า ดังนั้นเราจึงอาจได้รับประโยชน์จากการถดถอยที่แข็งแกร่งแทน

ขั้นตอนที่ 3: ดำเนินการถดถอยที่แข็งแกร่ง

ต่อไป ลองใช้ฟังก์ชัน rlm() เพื่อให้พอดีกับโมเดลการถดถอยที่มีประสิทธิภาพ:

 library (MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

เพื่อตรวจสอบว่าแบบจำลองการถดถอยที่แข็งแกร่งนี้เหมาะสมกับข้อมูลมากกว่าหรือไม่เมื่อเปรียบเทียบกับแบบจำลอง OLS เราสามารถคำนวณข้อผิดพลาดมาตรฐานที่เหลือของแต่ละรุ่นได้

ข้อผิดพลาดมาตรฐานคงเหลือ (RSE) เป็นวิธีการวัดค่าเบี่ยงเบนมาตรฐานของค่าคงเหลือในแบบจำลองการถดถอย ยิ่งค่า CSR ต่ำ โมเดลก็ยิ่งสามารถใส่ข้อมูลได้ดียิ่งขึ้น

รหัสต่อไปนี้แสดงวิธีคำนวณ RSE สำหรับแต่ละรุ่น:

 #find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

เราจะเห็นได้ว่า RSE ของตัวแบบการถดถอยแบบแข็งแกร่งนั้นต่ำกว่าตัวแบบการถดถอยกำลังสองน้อยที่สุดธรรมดามาก ซึ่งบอกเราว่าตัวแบบการถดถอยแบบรัดกุมให้ความเหมาะสมกับข้อมูลที่ดีกว่า

แหล่งข้อมูลเพิ่มเติม

วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน R
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
วิธีดำเนินการถดถอยพหุนามใน R