การถดถอยพหุนาม

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 2, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการถดถอยพหุนามในสถิติคืออะไร และดำเนินการอย่างไร นอกจากนี้ คุณจะสามารถดูตัวอย่างที่ใช้การถดถอยพหุนามได้

การถดถอยพหุนามคืออะไร?

การถดถอยพหุนาม หรือ การถดถอยพหุนาม เป็นแบบจำลองการถดถอยที่ความสัมพันธ์ระหว่างตัวแปรอิสระ X และตัวแปรตาม Y ถูกจำลองโดยใช้พหุนาม

ตัวอย่างเช่น สมการสำหรับแบบจำลองการถดถอยพหุนามกำลังสองคือ y=β ₀ +β ₁ x+β ₂ x ² +ε

การถดถอยพหุนามมีประโยชน์สำหรับการปรับชุดข้อมูลให้เหมาะสมซึ่งมีกราฟเป็นเส้นโค้งพหุนาม ดังนั้น หากดอทพล็อตของตัวอย่างข้อมูลมีรูปร่างเป็นรูปพาราโบลา การสร้างแบบจำลองการถดถอยกำลังสองจะดีกว่าการสร้างแบบจำลองการถดถอยเชิงเส้น ด้วยวิธีนี้ สมการแบบจำลองการถดถอยจะเข้ากับตัวอย่างข้อมูลได้ดีขึ้น

โปรดทราบว่าการถดถอยพหุนามเป็นการถดถอยแบบไม่เชิงเส้นประเภทหนึ่ง เช่นเดียวกับการถดถอยเอ็กซ์โปเนนเชียลและการถดถอยแบบลอการิทึม

สูตรการถดถอยพหุนาม

สมการสำหรับแบบจำลองการถดถอยพหุนามคือ y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

ทอง:

$y$

เป็นตัวแปรตาม
$x$

เป็นตัวแปรอิสระ
$\beta_0$

คือค่าคงที่ของสมการถดถอยพหุนาม
$\beta_i$

คือค่าสัมประสิทธิ์การถดถอยที่เกี่ยวข้องกับตัวแปร

$x^i$

.
$\bm{\varepsilon}$

นี่คือข้อผิดพลาดหรือค่าตกค้าง ซึ่งหมายถึงความแตกต่างระหว่างค่าที่สังเกตได้กับค่าที่ประเมินโดยแบบจำลอง

แล้วถ้าเรามีตัวอย่างที่มีผลรวมเป็น

$n$

จากการสังเกต เราสามารถเสนอแบบจำลองการถดถอยพหุนามในรูปแบบเมทริกซ์ได้:

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

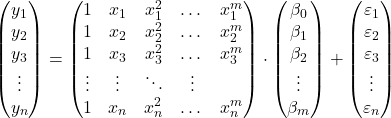
นิพจน์เมทริกซ์ด้านบนสามารถเขียนใหม่ได้โดยกำหนดตัวอักษรให้กับแต่ละเมทริกซ์:

$Y=X\beta+\varepsilon$

ดังนั้น เมื่อใช้ เกณฑ์กำลังสองน้อยที่สุด เราจะได้ สูตรสำหรับการประมาณค่าสัมประสิทธิ์ของแบบจำลองการถดถอยพหุนาม :

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

อย่างไรก็ตาม การคำนวณด้วยมือต้องใช้ความพยายามมากและใช้เวลานาน ดังนั้นจึงสะดวกกว่าในการใช้ซอฟต์แวร์คอมพิวเตอร์ (เช่น Minitab หรือ Excel) ซึ่งช่วยให้คุณดำเนินการแบบจำลองการถดถอยพหุนามได้เร็วขึ้นมาก

ตัวอย่างแบบจำลองการถดถอยพหุนาม

ตอนนี้เรารู้คำจำกัดความของการถดถอยพหุนามและวิธีการดำเนินการแล้ว เรามาดูตัวอย่างในชีวิตจริงเพื่อทำความเข้าใจแนวคิดนี้อย่างถ่องแท้กันดีกว่า

ประการแรก ควรจำไว้ว่าควรใช้แบบจำลองการถดถอยพหุนามเมื่อกราฟข้อมูลมีรูปร่างเป็นเส้นโค้งพหุนาม ตัวอย่างเช่น หากดอทพล็อตอยู่ในรูปของเส้นโค้งลูกบาศก์ เราจำเป็นต้องสร้างแบบจำลองการถดถอยพหุนามระดับที่สาม

อย่างที่คุณเห็นในภาพต่อไปนี้ ดอทพล็อตของข้อมูลของเรามีรูปร่างเป็นกำลังสอง เพราะเมื่อเราเพิ่มค่าของตัวแปรอิสระ ตัวแปรตามจะโตเร็วขึ้น ในกรณีนี้ มีการดำเนินการแบบจำลองการถดถอยเชิงเส้น และอย่างที่คุณเห็นว่ามันไม่พอดีกับจุดต่างๆ มากนัก เนื่องจากมีส่วนที่เส้นอยู่ต่ำกว่าจุดทั้งหมด และส่วนที่เส้นอยู่เหนือจุดเหล่านั้น

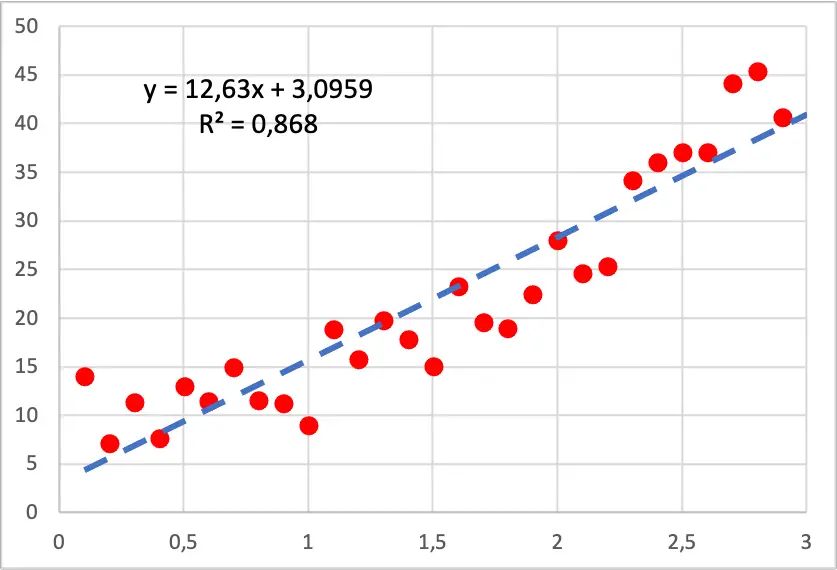
ในทางกลับกัน หากเราใช้แบบจำลองการถดถอยพหุนามกำลังสอง มันจะเหมาะกับข้อมูลตัวอย่างมากขึ้น ดังที่คุณเห็นในภาพด้านล่าง

นอกจากนี้ เมื่อพัฒนาแบบจำลองการถดถอยพหุนาม ค่าสัมประสิทธิ์การกำหนดจะดีขึ้นอย่างมากเนื่องจากเปลี่ยนจาก 86.80% เป็น 94.05% ดังนั้นโมเดลการถดถอยใหม่จึงอธิบายชุดข้อมูลได้ดีขึ้นมาก

ในทางกลับกัน สิ่งบ่งชี้อีกประการหนึ่งที่ว่าเราจำเป็นต้องทำการถดถอยพหุนามก็คือการวางแผนค่าคงเหลือ หากในการถดถอยเชิงเส้น กราฟของส่วนที่เหลือมีรูปร่างของพาราโบลาหรือพหุนามประเภทอื่น แบบจำลองการถดถอยพหุนามจะเหมาะกับข้อมูลที่ศึกษาดีกว่าอย่างแน่นอน

การถดถอยแบบไม่เชิงเส้นประเภทอื่น

การถดถอยแบบไม่เชิงเส้นมีสามประเภทหลักๆ:

การถดถอยพหุนาม – สมการแบบจำลองการถดถอยอยู่ในรูปแบบของพหุนาม
การถดถอยลอการิทึม : ใช้ลอการิทึมของตัวแปรอิสระ
การถดถอยเอ็กซ์โพเนนเชียล : พบตัวแปรอิสระในเลขชี้กำลังของสมการ

➤ ดู: การถดถอยลอการิทึม
➤ ดู: การถดถอยเอ็กซ์โปเนนเชียล

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม