การถดถอยลอการิทึม
บทความนี้จะอธิบายว่าการถดถอยแบบลอการิทึมคืออะไรและดำเนินการอย่างไร นอกจากนี้ คุณสามารถดูตัวอย่างการถดถอยลอการิทึมเพื่อให้เข้าใจแนวคิดนี้ได้อย่างถ่องแท้
การถดถอยลอการิทึมคืออะไร?
การถดถอยลอการิทึม เป็นแบบจำลองการถดถอยที่มีลอการิทึมอยู่ในสมการ โดยเฉพาะอย่างยิ่ง ในการถดถอยแบบลอการิทึม จะใช้ลอการิทึมของตัวแปรอิสระ ดังนั้นสมการสำหรับแบบจำลองการถดถอยลอการิทึมคือ y=a+b·ln(x)
การถดถอยแบบลอการิทึมมีประโยชน์อย่างมากสำหรับการปรับแบบจำลองการถดถอยให้เหมาะสม เมื่อข้อมูลตัวอย่างสร้างเส้นโค้งลอการิทึม เพื่อให้แบบจำลองการถดถอยเหมาะสมกับข้อมูลตัวอย่างได้ดีขึ้น ด้านล่างนี้เราจะดูว่าเมื่อใดที่คุณควรทำการถดถอยแบบลอการิทึม
ดังนั้น การถดถอยแบบลอการิทึมจึงเป็นการถดถอยแบบไม่เชิงเส้นประเภทหนึ่ง เช่นเดียวกับการถดถอยเอ็กซ์โปเนนเชียลและการถดถอยพหุนาม
สูตรการถดถอยลอการิทึม
แบบจำลองการถดถอยแบบลอการิทึมเกี่ยวข้องกับการใช้ลอการิทึมของตัวแปรอิสระ ดังนั้น สูตรสำหรับสมการของการถดถอยลอการิทึม คือ y=a+b·ln(x)
![]()
ทอง:
-

เป็นตัวแปรตาม
-

เป็นตัวแปรอิสระ
-

คือค่าสัมประสิทธิ์การถดถอย
โปรดทราบว่า y=a+b·ln(x) จริงๆ แล้วเป็นสมการของเส้นตรง แต่แทนที่จะอ้างถึงตัวแปรดั้งเดิม x และ y กลับอ้างถึงตัวแปร ln(x) และ y
เมื่อใดจึงจะทำการถดถอยลอการิทึม?
เราจำเป็นต้องดำเนินการถดถอยลอการิทึมเมื่อกราฟของข้อมูลตัวอย่างเป็นเส้นโค้งลอการิทึม นั่นคือเมื่อพล็อตของจุดคล้ายกับกราฟของฟังก์ชันลอการิทึม
ดูแผนภาพกระจายด้านล่าง มีการติดตั้งแบบจำลองการถดถอยเชิงเส้นเข้ากับชุดข้อมูล อย่างที่คุณเห็นเส้นนี้ไม่ใช่การประมาณข้อมูลที่ไม่ดี แต่ถ้าคุณระวัง ค่าที่จุดเริ่มต้นของกราฟจะเพิ่มขึ้นเร็วกว่าจุดสิ้นสุด ดังนั้น เส้นจึงไม่ตรงกับการสังเกตอย่างสมบูรณ์ .
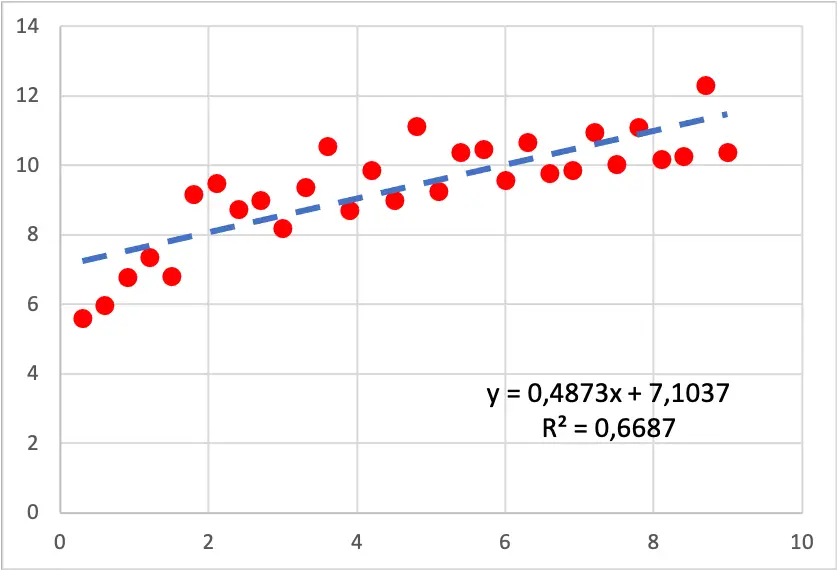
ดังนั้นจึงคุ้มค่าที่จะลองสร้างแบบจำลองการถดถอยแบบลอการิทึม เพราะดูเหมือนว่าข้อมูลจะเป็นไปตามเส้นโค้งลอการิทึม ผลลัพธ์ที่ได้จากแบบจำลองการถดถอยลอการิทึมมีดังนี้

ดังที่คุณเห็นในกราฟก่อนหน้านี้ ผลลัพธ์ของแบบจำลองการถดถอยแบบลอการิทึมจะเหมาะกับข้อมูลตัวอย่างมากกว่า อันที่จริง ค่าสัมประสิทธิ์การตัดสินใจเพิ่มขึ้นจาก 66.87% เป็น 80.05% ดังนั้นแบบจำลองจึงสามารถอธิบายตัวอย่างข้อมูลได้ดีขึ้น ดังนั้นในกรณีนี้ ควรใช้การถดถอยโลจิสติกเพื่อค้นหาสมการที่ประมาณค่าข้อมูลจะดีกว่า
การถดถอยแบบไม่เชิงเส้นประเภทอื่น
กรณีที่พบบ่อยที่สุดสามกรณีของการถดถอยแบบไม่เชิงเส้นคือ:
- การถดถอยลอการิทึม : ใช้ลอการิทึมของตัวแปรอิสระ
- การถดถอยเอ็กซ์โพเนนเชียล : ตัวแปรอิสระคือเลขชี้กำลังของสมการ
- การถดถอยพหุนาม : สมการแบบจำลองการถดถอยจะอยู่ในรูปของพหุนาม