การถดถอยองค์ประกอบหลักใน r (ทีละขั้นตอน)

เมื่อกำหนดชุดของตัวแปรทำนาย p และตัวแปร ตอบสนอง การถดถอยเชิงเส้นพหุคูณ จะใช้วิธีที่เรียกว่า กำลังสองน้อยที่สุด เพื่อลดผลรวมที่เหลือของกำลังสอง (RSS):

RSS = Σ(ฉัน _ฉัน – ŷ _ฉัน ) ²

ทอง:

• Σ : สัญลักษณ์กรีกหมายถึง ผลรวม
• y _i : ค่าตอบสนองจริงสำหรับการสังเกต ^{ครั้งที่ 3}
• ŷ _i : ค่าตอบสนองที่คาดการณ์ไว้ตามแบบจำลองการถดถอยเชิงเส้นพหุคูณ

อย่างไรก็ตาม เมื่อตัวแปรทำนายมีความสัมพันธ์กันสูง ความเป็นหลายคอลลิเนียร์ อาจกลายเป็นปัญหาได้ ซึ่งอาจทำให้การประมาณค่าสัมประสิทธิ์แบบจำลองไม่น่าเชื่อถือและแสดงความแปรปรวนสูง

วิธีหนึ่งที่จะหลีกเลี่ยงปัญหานี้คือการใช้ การถดถอยองค์ประกอบหลัก ซึ่งจะค้นหาชุดค่าผสมเชิงเส้น M (เรียกว่า “ส่วนประกอบหลัก”) ของตัวทำนาย p ดั้งเดิม จากนั้นใช้กำลังสองน้อยที่สุดเพื่อให้พอดีกับแบบจำลองการถดถอยเชิงเส้นโดยใช้ส่วนประกอบหลักเป็นตัวทำนาย

บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีการดำเนินการถดถอยส่วนประกอบหลักใน R

ขั้นตอนที่ 1: โหลดแพ็คเกจที่จำเป็น

วิธีที่ง่ายที่สุดในการดำเนินการถดถอยส่วนประกอบหลักใน R คือการใช้ฟังก์ชันในแพ็คเกจ pls

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

ขั้นตอนที่ 2: ปรับโมเดล PCR

สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูล R ในตัวที่เรียกว่า mtcars ซึ่งมีข้อมูลเกี่ยวกับรถยนต์ประเภทต่างๆ:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

สำหรับตัวอย่างนี้ เราจะปรับโมเดลการถดถอยส่วนประกอบหลัก (PCR) โดยใช้ hp เป็น ตัวแปรการตอบสนอง และตัวแปรต่อไปนี้เป็นตัวแปรทำนาย:

• mpg
• แสดง
• อึ
• น้ำหนัก
• คิววินาที

รหัสต่อไปนี้แสดงวิธีปรับโมเดล PCR ให้พอดีกับข้อมูลนี้ สังเกตข้อโต้แย้งต่อไปนี้:

• scale=TRUE : สิ่งนี้จะบอก R ว่าตัวแปรทำนายแต่ละตัวควรได้รับการปรับขนาดให้มีค่าเฉลี่ยเป็น 0 และค่าเบี่ยงเบนมาตรฐานเป็น 1 สิ่งนี้ทำให้แน่ใจได้ว่าไม่มีตัวแปรตัวทำนายใดที่มีอิทธิพลมากเกินไปในแบบจำลองหากวัดในหน่วยที่แตกต่างกัน .
• validation=”CV” : สิ่งนี้จะบอก R ให้ใช้ การตรวจสอบข้าม k-fold เพื่อประเมินประสิทธิภาพของโมเดล โปรดทราบว่าสิ่งนี้ใช้ k=10 เท่าเป็นค่าเริ่มต้น โปรดทราบว่าคุณสามารถระบุ “LOOCV” แทนเพื่อทำการ ตรวจสอบข้ามแบบ Leave-One-Out

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- pcr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

ขั้นตอนที่ 3: เลือกจำนวนส่วนประกอบหลัก

เมื่อเราปรับเปลี่ยนโมเดลแล้ว เราจำเป็นต้องพิจารณาว่าส่วนประกอบหลักจำนวนเท่าใดที่ควรค่าแก่การรักษาไว้

ในการดำเนินการนี้ เพียงดูที่ค่าความคลาดเคลื่อนกำลังสองเฉลี่ยของรูทการทดสอบ (ทดสอบ RMSE) ที่คำนวณโดยการตรวจสอบความถูกต้องของ k-cross:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: svdpc
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 44.56 35.64 35.83 36.23 36.67
adjCV 69.66 44.44 35.27 35.43 35.80 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 69.83 89.35 95.88 98.96 100.00
hp 62.38 81.31 81.96 81.98 82.03

ผลลัพธ์มีตารางที่น่าสนใจสองตาราง:

1. การตรวจสอบความถูกต้อง: RMSEP

ตารางนี้บอกเราถึงการทดสอบ RMSE ที่คำนวณโดยการตรวจสอบข้าม k-fold เราสามารถเห็นสิ่งต่อไปนี้:

• หากเราใช้เฉพาะคำดั้งเดิมในโมเดล RMSE ของการทดสอบคือ 69.66
• หากเราเพิ่มองค์ประกอบหลักแรก การทดสอบ RMSE จะลดลงเหลือ 44.56
• หากเราเพิ่มองค์ประกอบหลักตัวที่สอง การทดสอบ RMSE จะลดลงเหลือ 35.64

เราจะเห็นได้ว่าการเพิ่มส่วนประกอบหลักเพิ่มเติมส่งผลให้ RMSE ของการทดสอบเพิ่มขึ้น ดังนั้น จึงดูเหมือนว่าเป็นการเหมาะสมที่สุดที่จะใช้ส่วนประกอบหลักเพียงสองส่วนในแบบจำลองขั้นสุดท้าย

2. การฝึกอบรม: อธิบาย % ของความแปรปรวน

ตารางนี้บอกเราถึงเปอร์เซ็นต์ของความแปรปรวนในตัวแปรตอบสนองที่อธิบายโดยองค์ประกอบหลัก เราสามารถเห็นสิ่งต่อไปนี้:

• การใช้เพียงองค์ประกอบหลักแรกเท่านั้น เราสามารถอธิบายความแปรผันของตัวแปรตอบสนองได้ 69.83%
• ด้วยการเพิ่มองค์ประกอบหลักที่สอง เราสามารถอธิบายความแปรผันของตัวแปรตอบสนองได้ 89.35%

โปรดทราบว่าเรายังคงสามารถอธิบายความแปรปรวนได้มากขึ้นโดยใช้องค์ประกอบหลักมากขึ้น แต่เราเห็นว่าการเพิ่มองค์ประกอบหลักมากกว่า 2 องค์ประกอบจริงๆ แล้วไม่ได้เพิ่มเปอร์เซ็นต์ของความแปรปรวนที่อธิบายไว้มากนัก

นอกจากนี้เรายังสามารถเห็นภาพการทดสอบ RMSE (พร้อมกับการทดสอบ MSE และ R-squared) ที่เป็นฟังก์ชันของจำนวนส่วนประกอบหลักโดยใช้ฟังก์ชัน validationplot()

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type="MSEP")
validationplot(model, val.type="R2") 

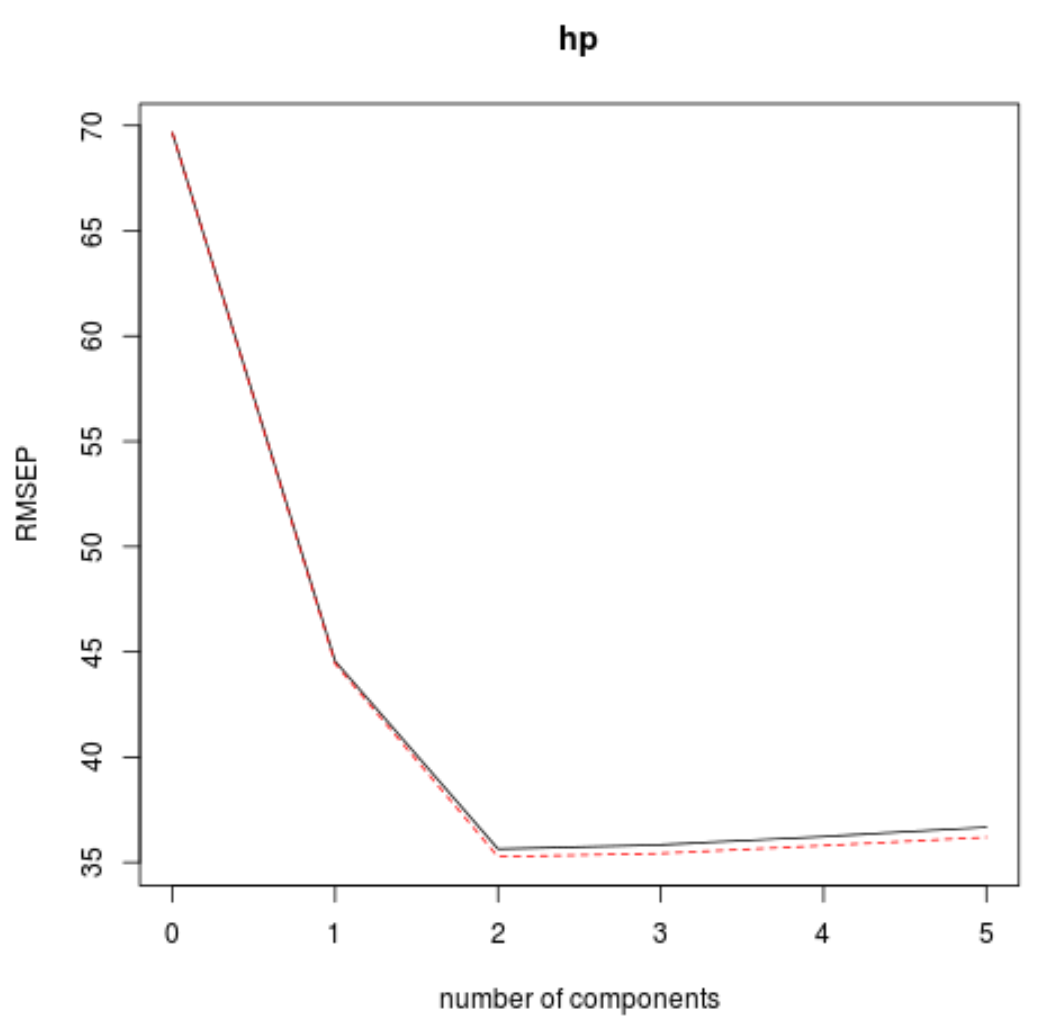
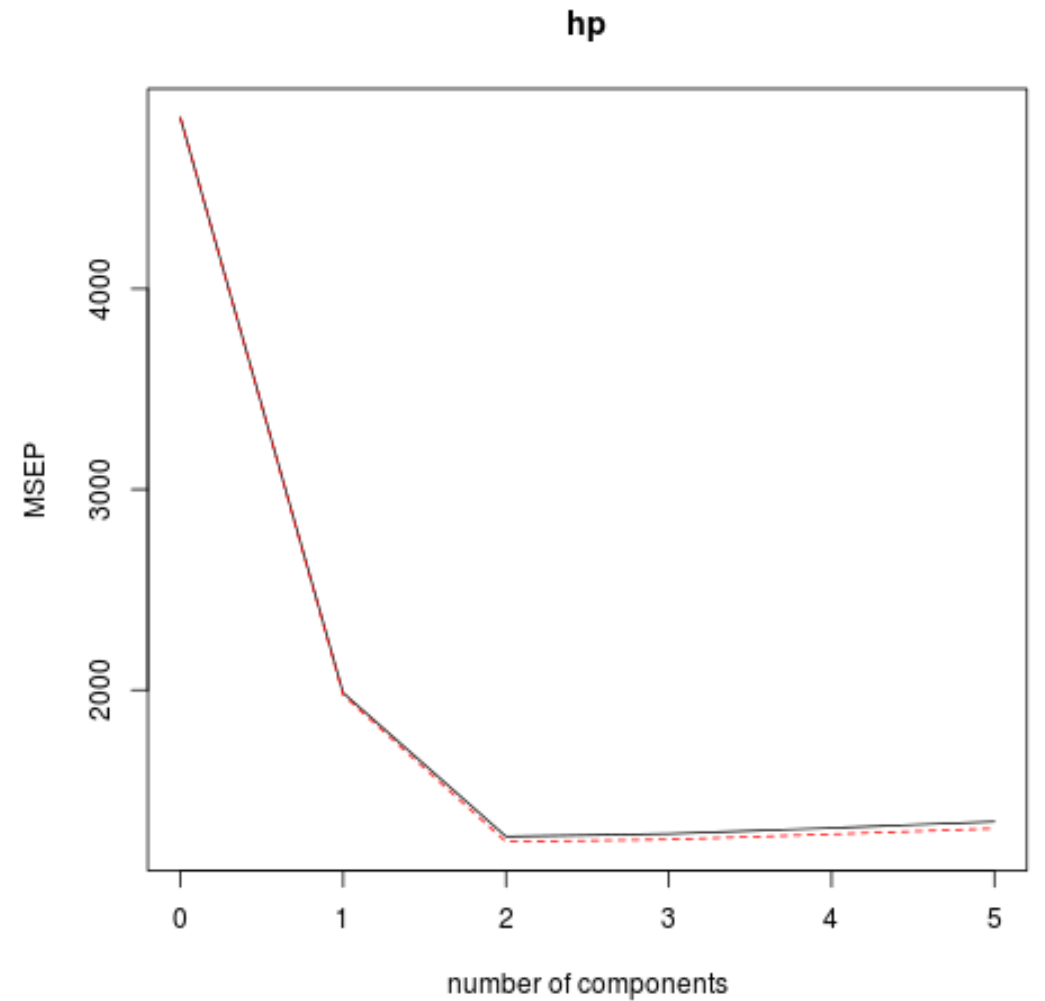
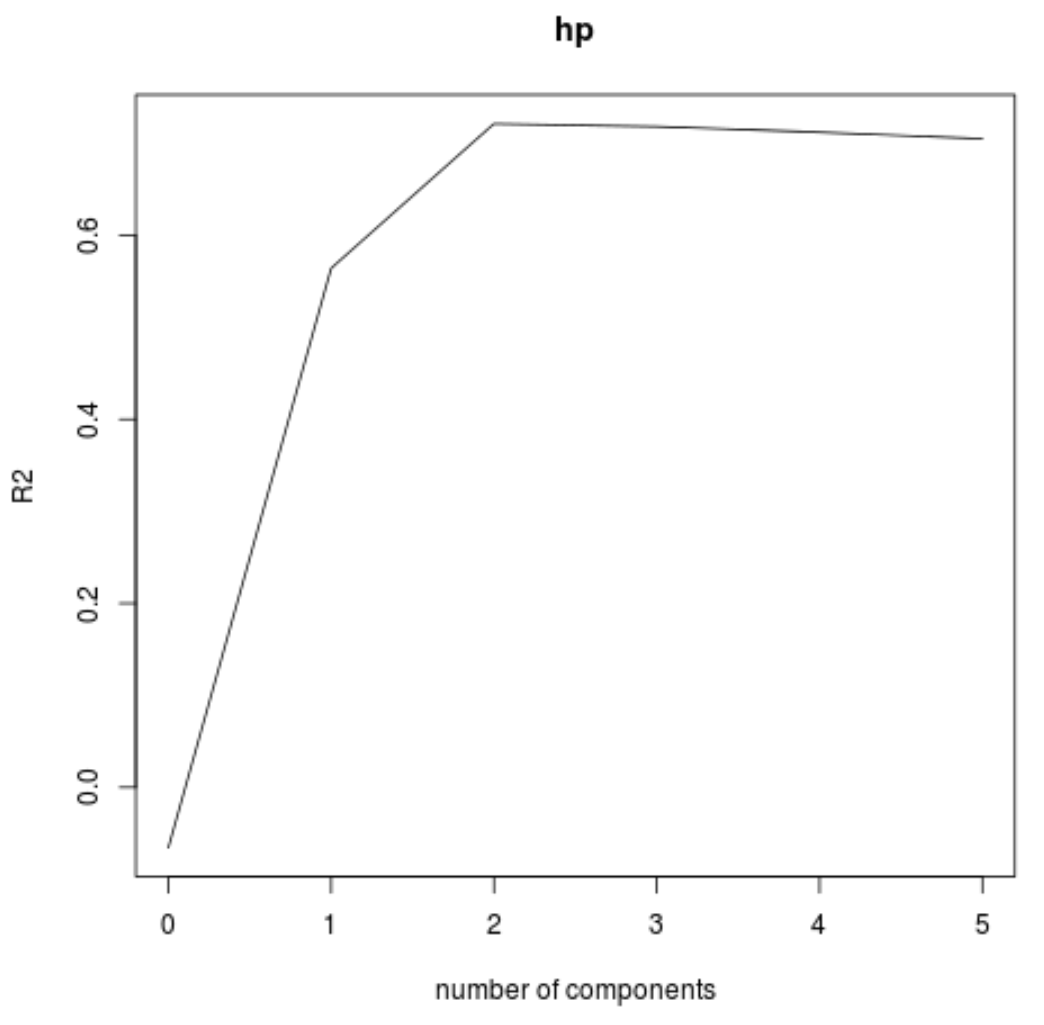
ในแต่ละกราฟ เราจะเห็นว่าโมเดลพอดีได้รับการปรับปรุงโดยการเพิ่มองค์ประกอบหลักสองรายการ แต่มีแนวโน้มที่จะลดลงเมื่อเราเพิ่มองค์ประกอบหลักเพิ่มเติม

ดังนั้นแบบจำลองที่เหมาะสมที่สุดจึงมีเพียงองค์ประกอบหลักสองส่วนแรกเท่านั้น

ขั้นตอนที่ 4: ใช้แบบจำลองสุดท้ายเพื่อคาดการณ์

เราสามารถใช้แบบจำลอง PCR ส่วนประกอบสองหลักสุดท้ายเพื่อคาดการณ์เกี่ยวกับการสังเกตใหม่

รหัสต่อไปนี้แสดงวิธีแยกชุดข้อมูลดั้งเดิมออกเป็นชุดการฝึกและชุดทดสอบ และใช้แบบจำลอง PCR ที่มีองค์ประกอบหลักสองส่วนเพื่อคาดการณ์ชุดทดสอบ

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- pcr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 56.86549

เราจะเห็นว่า RMSE ของการทดสอบกลายเป็น 56.86549 นี่คือค่าเบี่ยงเบนเฉลี่ยระหว่างค่า HP ที่คาดการณ์ไว้กับค่า HP ที่สังเกตได้สำหรับการสังเกตชุดทดสอบ

การใช้งานโค้ด R อย่างเต็มรูปแบบในตัวอย่างนี้สามารถพบได้ ที่นี่