รู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นอย่างง่าย

การถดถอยเชิงเส้นอย่างง่าย เป็นวิธีการทางสถิติที่คุณสามารถใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรสองตัว นั่นคือ x และ y

ตัวแปร x เรียกว่า ตัวแปรทำนาย

ตัวแปรอื่น y เรียกว่า ตัวแปรตอบสนอง

ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งมีน้ำหนักและส่วนสูงเท่ากับบุคคล 7 คน:

ให้ น้ำหนัก เป็นตัวแปรทำนาย และให้ ความสูง เป็นตัวแปรตอบสนอง

หากเราสร้างกราฟตัวแปรทั้งสองนี้โดยใช้แผนภาพกระจาย โดยมีน้ำหนักบนแกน x และความสูงบนแกน y จะได้หน้าตาดังนี้:

สมมติว่าเราต้องการเข้าใจความสัมพันธ์ระหว่างน้ำหนักและส่วนสูง จากแผนภาพกระจาย เราจะเห็นได้อย่างชัดเจนว่าเมื่อน้ำหนักเพิ่มขึ้น ความสูงก็มีแนวโน้มที่จะเพิ่มขึ้นด้วย แต่ใน การหาความ สัมพันธ์ระหว่างน้ำหนักและส่วนสูงจริงๆ เราจำเป็นต้องใช้การถดถอยเชิงเส้น

เมื่อใช้การถดถอยเชิงเส้น เราสามารถค้นหาเส้นที่ “เหมาะสม” กับข้อมูลของเราได้ดีที่สุด เส้นนี้เรียกว่า เส้นถดถอยกำลังสองน้อยที่สุด และสามารถใช้เพื่อช่วยให้เราเข้าใจความสัมพันธ์ระหว่างน้ำหนักและส่วนสูง

โดยปกติ คุณจะใช้ซอฟต์แวร์เช่น Microsoft Excel, SPSS หรือเครื่องคิดเลขกราฟเพื่อค้นหาสมการของเส้นนี้

สูตรสำหรับบรรทัดที่เหมาะสมที่สุดเขียนไว้:

ŷ = ข ₀ + ข ₁ x

โดยที่ ŷ คือค่าทำนายของตัวแปรตอบสนอง b ₀ คือจุดตัด b ₁ คือสัมประสิทธิ์การถดถอย และ x คือค่าของตัวแปรทำนาย

ที่เกี่ยวข้อง: 4 ตัวอย่างการใช้การถดถอยเชิงเส้นในชีวิตจริง

ค้นหา “สายที่เหมาะสมที่สุด”

สำหรับตัวอย่างนี้ เราสามารถเสียบข้อมูลของเราเข้ากับ เครื่องคำนวณการถดถอยเชิงเส้นทางสถิติ แล้วกด Calculate :

เครื่องคิดเลขจะค้นหา เส้นถดถอยกำลังสองน้อยที่สุด โดยอัตโนมัติ:

ŷ = 32.7830 + 0.2001x

หากเราซูมออกจากแผนภาพกระจายก่อนหน้าของเรา และเพิ่มเส้นนี้ลงในกราฟ หน้าตาจะเป็นอย่างไร:

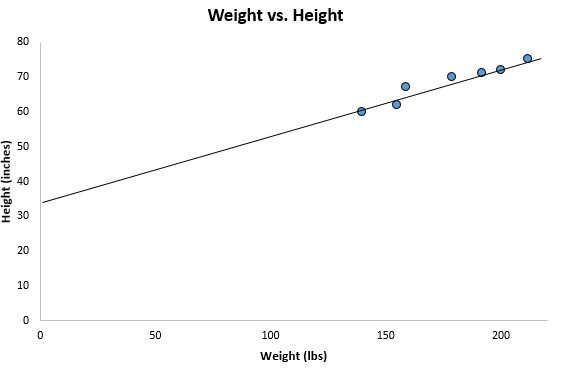
สังเกตว่าจุดข้อมูลของเรากระจัดกระจายอยู่ใกล้เส้นนี้อย่างไร อันที่จริง เส้นการถดถอยกำลังสองน้อยที่สุดนี้เป็นเส้นที่เหมาะสมที่สุดกับข้อมูลของเรา ในบรรดาเส้นที่เป็นไปได้ทั้งหมดที่เราสามารถวาดได้

วิธีตีความเส้นถดถอยกำลังสองน้อยที่สุด

ต่อไปนี้คือวิธีตีความเส้นถดถอยกำลังสองน้อยที่สุด: ŷ = 32.7830 + 0.2001x

_ข0 = 32.7830 . ซึ่งหมายความว่าเมื่อ น้ำหนัก ตัวแปรทำนายเป็นศูนย์ปอนด์ ความสูงที่คาดการณ์คือ 32.7830 นิ้ว บางครั้งค่าของ b ₀ อาจเป็นประโยชน์ที่จะรู้ แต่ในตัวอย่างนี้ มันไม่สมเหตุสมผลเลยที่จะตีความ b ₀ เนื่องจากบุคคลไม่สามารถมีน้ำหนักเป็นศูนย์ปอนด์ได้

_ข1 = 0.2001 . ซึ่งหมายความว่าการเพิ่ม x หนึ่งหน่วยสัมพันธ์กับการเพิ่มขึ้น 0.2001 หน่วยใน y ในกรณีนี้ น้ำหนักที่เพิ่มขึ้นหนึ่งปอนด์สัมพันธ์กับความสูงที่เพิ่มขึ้น 0.2001 นิ้ว

วิธีใช้เส้นถดถอยกำลังสองน้อยที่สุด

การใช้เส้นถดถอยกำลังสองน้อยที่สุดนี้ เราสามารถตอบคำถามต่างๆ เช่น:

สำหรับคนที่หนัก 170 ปอนด์ เราควรคาดหวังให้เขาสูงแค่ไหน?

เพื่อตอบคำถามนี้ เราสามารถแทรก 170 ลงในเส้นการถดถอยสำหรับ x แล้วแก้หา y:

ŷ = 32.7830 + 0.2001(170) = 66.8 นิ้ว

สำหรับคนที่หนัก 150 ปอนด์ เราควรคาดหวังให้เขาสูงแค่ไหน?

เพื่อตอบคำถามนี้ เราสามารถแทรก 150 ลงในเส้นการถดถอยสำหรับ x และแก้หา y:

ŷ = 32.7830 + 0.2001(150) = 62.798 นิ้ว

ข้อควรระวัง: เมื่อใช้สมการถดถอยตอบคำถามลักษณะนี้ ต้องแน่ใจว่าใช้เฉพาะค่าสำหรับตัวแปรทำนายที่อยู่ในช่วงของตัวแปรทำนายในชุดข้อมูลเท่านั้น จุดกำเนิดที่เราใช้สร้างเส้นถดถอยกำลังสองน้อยที่สุด ตัวอย่างเช่น น้ำหนักในชุดข้อมูลของเราอยู่ระหว่าง 140 ถึง 212 ปอนด์ ดังนั้นจึงสมเหตุสมผลที่จะตอบคำถามเกี่ยวกับส่วนสูงที่คาดหวังเมื่อน้ำหนักอยู่ระหว่าง 140 ถึง 212 ปอนด์

ค่าสัมประสิทธิ์การตัดสินใจ

วิธีหนึ่งในการวัดว่าเส้นการถดถอยกำลังสองน้อยที่สุด “พอดี” กับข้อมูลได้ดีเพียงใด คือการใช้ สัมประสิทธิ์การกำหนด ซึ่งแสดงแทน R ²

ค่าสัมประสิทธิ์การกำหนดคือสัดส่วนของความแปรปรวนในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรทำนาย

ค่าสัมประสิทธิ์การกำหนดอาจแตกต่างกันไปตั้งแต่ 0 ถึง 1 ค่า 0 บ่งชี้ว่าตัวแปรการตอบสนองไม่สามารถอธิบายได้ด้วยตัวแปรทำนายเลย ค่า 1 บ่งชี้ว่าตัวแปรตัวทำนายสามารถอธิบายตัวแปรตอบสนองได้อย่างสมบูรณ์แบบโดยไม่มีข้อผิดพลาด

R ² ระหว่าง 0 ถึง 1 บ่งชี้ขอบเขตที่ตัวแปรตอบสนองสามารถอธิบายได้ด้วยตัวแปรทำนาย ตัวอย่างเช่น R ² ของ 0.2 บ่งชี้ว่า 20% ของความแปรปรวนในตัวแปรตอบสนองสามารถอธิบายได้ด้วยตัวแปรทำนาย R ² ของ 0.77 บ่งชี้ว่า 77% ของความแปรปรวนในตัวแปรตอบสนองสามารถอธิบายได้ด้วยตัวแปรทำนาย

โปรดทราบว่าในผลลัพธ์ก่อนหน้านี้ เราได้รับ R ² เป็น 0.9311 ซึ่งบ่งชี้ว่า 93.11% ของความแปรปรวนในความสูงสามารถอธิบายได้ด้วยตัวแปรทำนายน้ำหนัก:

ข้อมูลนี้บอกเราว่าน้ำหนักเป็นตัวบ่งชี้ส่วนสูงได้ดีมาก

สมมติฐานการถดถอยเชิงเส้น

เพื่อให้ผลลัพธ์ของแบบจำลองการถดถอยเชิงเส้นถูกต้องและเชื่อถือได้ เราต้องตรวจสอบว่าเป็นไปตามสมมติฐานสี่ประการต่อไปนี้:

1. ความสัมพันธ์เชิงเส้น: มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรอิสระ x และตัวแปรตาม y

2. ความเป็นอิสระ: ส่วนที่เหลือเป็นอิสระ โดยเฉพาะอย่างยิ่งไม่มีความสัมพันธ์ระหว่างข้อมูลตกค้างติดต่อกันในข้อมูลอนุกรมเวลา

3. ความเป็นเนื้อเดียวกัน: สารตกค้างมีความแปรปรวนคงที่ในแต่ละระดับของ x

4. Normality: โมเดลที่เหลือมีการกระจายตามปกติ

หากไม่เป็นไปตามสมมติฐานเหล่านี้ตั้งแต่หนึ่งข้อขึ้นไป ผลลัพธ์ของการถดถอยเชิงเส้นของเราอาจไม่น่าเชื่อถือหรืออาจทำให้เข้าใจผิดได้

โปรดดู บทความนี้ สำหรับคำอธิบายของแต่ละสมมติฐาน วิธีตรวจสอบว่าเป็นไปตามสมมติฐานหรือไม่ และต้องทำอย่างไรหากไม่เป็นไปตามสมมติฐาน