การถดถอยเชิงเส้นอย่างง่าย
บทความนี้จะอธิบายว่าการถดถอยเชิงเส้นอย่างง่ายคืออะไรในสถิติและดำเนินการอย่างไร ในทำนองเดียวกัน คุณจะพบว่าแบบฝึกหัดการถดถอยเชิงเส้นแบบง่ายๆ ได้รับการแก้ไข และยังมีเครื่องคำนวณการถดถอยเชิงเส้นแบบง่ายๆ ทางออนไลน์ด้วย
การถดถอยเชิงเส้นอย่างง่ายคืออะไร?
การถดถอยเชิงเส้นอย่างง่าย เป็นแบบจำลองทางสถิติที่ใช้สร้างความสัมพันธ์ของตัวแปรอิสระ และเราพยายามประมาณความสัมพันธ์ระหว่างตัวแปรทั้งสอง
ดังนั้น การถดถอยเชิงเส้นอย่างง่ายจึงใช้เพื่อค้นหาสมการที่เกี่ยวข้องกับตัวแปรสองตัวเชิงเส้นตรง ตามตรรกะแล้ว ความสัมพันธ์ระหว่างตัวแปรทั้งสองจะต้องเป็นแบบเส้นตรง ไม่เช่นนั้นจะต้องใช้แบบจำลองการถดถอยประเภทอื่น
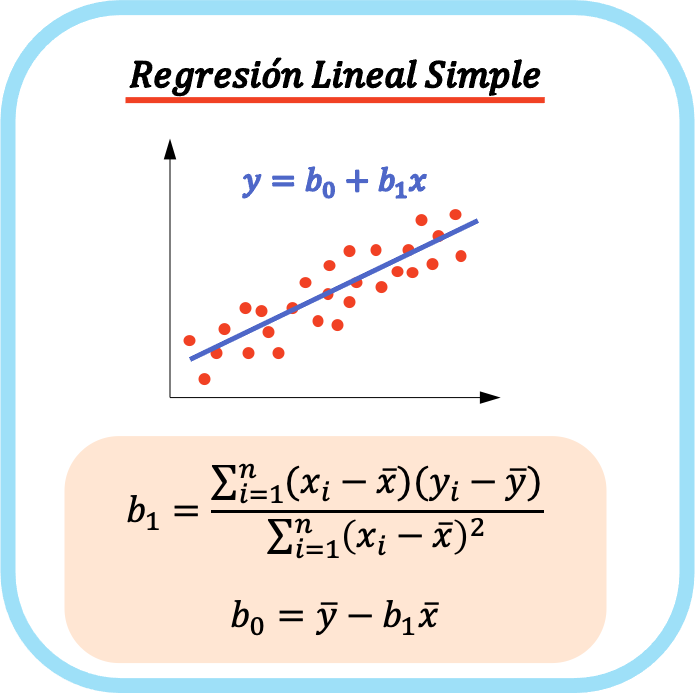
สมการของแบบจำลองการถดถอยเชิงเส้นอย่างง่ายประกอบด้วยค่าสัมประสิทธิ์ 2 ค่า ได้แก่ ค่าคงที่ของสมการ (b 0 ) และค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรทั้งสอง (b 1 ) ดังนั้น สมการสำหรับแบบจำลองการถดถอยเชิงเส้นอย่างง่ายคือ y=b 0 +b 1 x
![]()
สมการของการถดถอยเชิงเส้นอย่างง่ายจะแสดงกราฟเป็นเส้นตรง ดังนั้นสัมประสิทธิ์ b 0 คือจุดตัด และสัมประสิทธิ์ b 1 คือความชันของเส้นตรง
สูตรการถดถอยเชิงเส้นอย่างง่าย
สูตรในการคำนวณค่าสัมประสิทธิ์ของการถดถอยเชิงเส้นอย่างง่าย มีดังนี้:
👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่าสัมประสิทธิ์ของการถดถอยเชิงเส้นอย่างง่ายสำหรับชุดข้อมูลใดๆ
แน่นอนว่าสมการที่เกิดจากแบบจำลองการถดถอยเชิงเส้นอย่างง่ายจะไม่สามารถคาดเดาค่าที่แน่นอนของการสังเกตทั้งหมดได้ เนื่องจากแบบจำลองนี้พยายามค้นหาสมการที่ประมาณความสัมพันธ์ระหว่างตัวแปรทั้งสองเท่านั้น ดังนั้นส่วนที่เหลือจึงถูกกำหนดให้เป็นความแตกต่างระหว่างมูลค่าที่แท้จริงกับมูลค่าที่ประมาณโดยแบบจำลองการถดถอยเชิงเส้น
![]()
โปรดทราบว่าเป้าหมายของแบบจำลองการถดถอยเชิงเส้นอย่างง่ายคือการลดกำลังสองของส่วนที่เหลือให้เหลือน้อยที่สุด กล่าวคือ การถดถอยเชิงเส้นอย่างง่ายจะขึ้นอยู่กับเกณฑ์ กำลังสองน้อยที่สุด
ตัวอย่างที่เป็นรูปธรรมของการถดถอยเชิงเส้นอย่างง่าย
เพื่อทำความเข้าใจวิธีการถดถอยเชิงเส้นอย่างง่ายให้เสร็จสิ้น ต่อไปนี้คือตัวอย่างเชิงปฏิบัติทีละขั้นตอน ซึ่งคำนวณสมการของแบบจำลองการถดถอยเชิงเส้นอย่างง่ายจากชุดข้อมูลทางสถิติ
- หลังจากทำข้อสอบสถิติแล้ว นักเรียน 5 คนถูกถามว่าพวกเขาใช้เวลาเรียนกับการสอบกี่ชั่วโมง ข้อมูลแสดงอยู่ในตารางด้านล่าง ทำแบบจำลองการถดถอยเชิงเส้นอย่างง่ายของข้อมูลทางสถิติที่รวบรวมมาเพื่อเชื่อมโยงชั่วโมงเรียนกับเกรดที่ได้รับเชิงเส้นตรง

ในการทำแบบจำลองการถดถอยเชิงเส้นอย่างง่าย เราต้องกำหนดค่าสัมประสิทธิ์ b 0 และ b 1 ของสมการ และด้วยเหตุนี้ เราต้องใช้สูตรที่เห็นในส่วนด้านบน
อย่างไรก็ตาม ในการใช้สูตรการถดถอยเชิงเส้นอย่างง่าย อันดับแรกเราต้องคำนวณค่าเฉลี่ยของตัวแปรอิสระและค่าเฉลี่ยของตัวแปรตาม:
![Rendered by QuickLaTeX.com \begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7a7aa6f1f20fa4ff0d61a2ad0dd2ea1f_l3.png)
ตอนนี้เรารู้ค่าเฉลี่ยของตัวแปรแล้ว เราก็คำนวณค่าสัมประสิทธิ์ b 1 ของแบบจำลองโดยใช้สูตรที่เกี่ยวข้อง:
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c9d90c766487cd7b6924e6b23d2d9c78_l3.png)
สุดท้ายเราคำนวณค่าสัมประสิทธิ์ b 0 ของแบบจำลองโดยใช้สูตรที่เกี่ยวข้อง:
![Rendered by QuickLaTeX.com \begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c72e6b89a75681a88cf751ca39079240_l3.png)
กล่าวโดยสรุป สมการสำหรับแบบจำลองการถดถอยเชิงเส้นอย่างง่ายของปัญหาคือ:
![]()
ด้านล่างนี้ คุณจะเห็นการแสดงข้อมูลตัวอย่างแบบกราฟิกตลอดจนเส้นตรงของแบบจำลองการถดถอยเชิงเส้นอย่างง่าย:

สุดท้ายนี้ เมื่อเราคำนวณสมการของแบบจำลองการถดถอยเชิงเส้นอย่างง่ายแล้ว สิ่งที่เหลืออยู่คือการตีความผลลัพธ์ที่ได้รับ สำหรับสิ่งนี้ การคำนวณค่าสัมประสิทธิ์การกำหนดแบบจำลองการถดถอยเป็นสิ่งสำคัญ คุณสามารถดูวิธีการได้โดยการค้นหาบทความที่เกี่ยวข้องในเว็บไซต์ของเรา
สมมติฐานการถดถอยเชิงเส้นอย่างง่าย
ในการที่จะทำการถดถอยเชิงเส้นอย่างง่าย จะต้องเป็นไปตามสมมติฐานต่อไปนี้:
- ความเป็นอิสระ : สิ่งตกค้างที่สังเกตได้จะต้องเป็นอิสระจากกัน วิธีทั่วไปในการตรวจสอบความเป็นอิสระของโมเดลคือการเพิ่มการสุ่มให้กับกระบวนการสุ่มตัวอย่าง
- Homoscedasticity : ความแปรปรวนของสารตกค้างจะต้องมีความสม่ำเสมอ กล่าวคือ ความแปรปรวนของสารตกค้างจะต้องคงที่
- ภาวะปกติ : ส่วนที่เหลือจะต้องกระจายตามปกติ หรืออีกนัยหนึ่ง จะต้องเป็นไปตามการแจกแจงแบบปกติด้วยค่าเฉลี่ย 0
- ความเป็นเชิงเส้น – ความสัมพันธ์ระหว่างตัวแปรอิสระและตัวแปรตามควรเป็นแบบเส้นตรง
เครื่องคำนวณการถดถอยเชิงเส้นอย่างง่าย
ใส่ข้อมูลตัวอย่างลงในเครื่องคิดเลขด้านล่างเพื่อให้พอดีกับแบบจำลองการถดถอยเชิงเส้นอย่างง่ายระหว่างตัวแปรสองตัว คุณต้องแยกคู่ข้อมูลเพื่อให้ในกล่องแรกมีเพียงค่าของตัวแปรอิสระ X และในกล่องที่สองมีเพียงค่าของตัวแปรตาม Y
ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม
การถดถอยเชิงเส้นแบบง่ายและพหุคูณ
สุดท้าย เราจะดูว่าอะไรคือความแตกต่างระหว่างการถดถอยเชิงเส้นอย่างง่ายและการถดถอยเชิงเส้นพหุคูณ เนื่องจากการถดถอยเชิงเส้นสองประเภทที่ใช้บ่อยในสถิติ
การถดถอยเชิงเส้นพหุคูณ ทำให้สามารถเชื่อมโยงตัวแปรอธิบายตั้งแต่สองตัวขึ้นไปเข้ากับตัวแปรตอบสนองทางคณิตศาสตร์ได้ กล่าวคือ ในการถดถอยเชิงเส้นพหุคูณ โมเดลจะถูกสร้างขึ้นโดยมีตัวแปรอิสระอย่างน้อยสองตัว
ดังนั้น ความแตกต่างระหว่างการถดถอยเชิงเส้นอย่างง่ายและการถดถอยเชิงเส้นพหุคูณ คือจำนวนตัวแปรอิสระ ในการถดถอยเชิงเส้นอย่างง่าย จะมีตัวแปรอิสระเพียงตัวเดียว ในขณะที่ในการถดถอยเชิงเส้นหลายตัวจะมีตัวแปรอิสระสองตัวขึ้นไป